Μοριοδότηση 2022
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(δ\)
Α3 - \(γ\)
Α4 - \(β\)
Α5: \(Λ - Σ - Λ - Σ - Σ\)
Θέμα Β
Β1 - \((i)-2-6\)
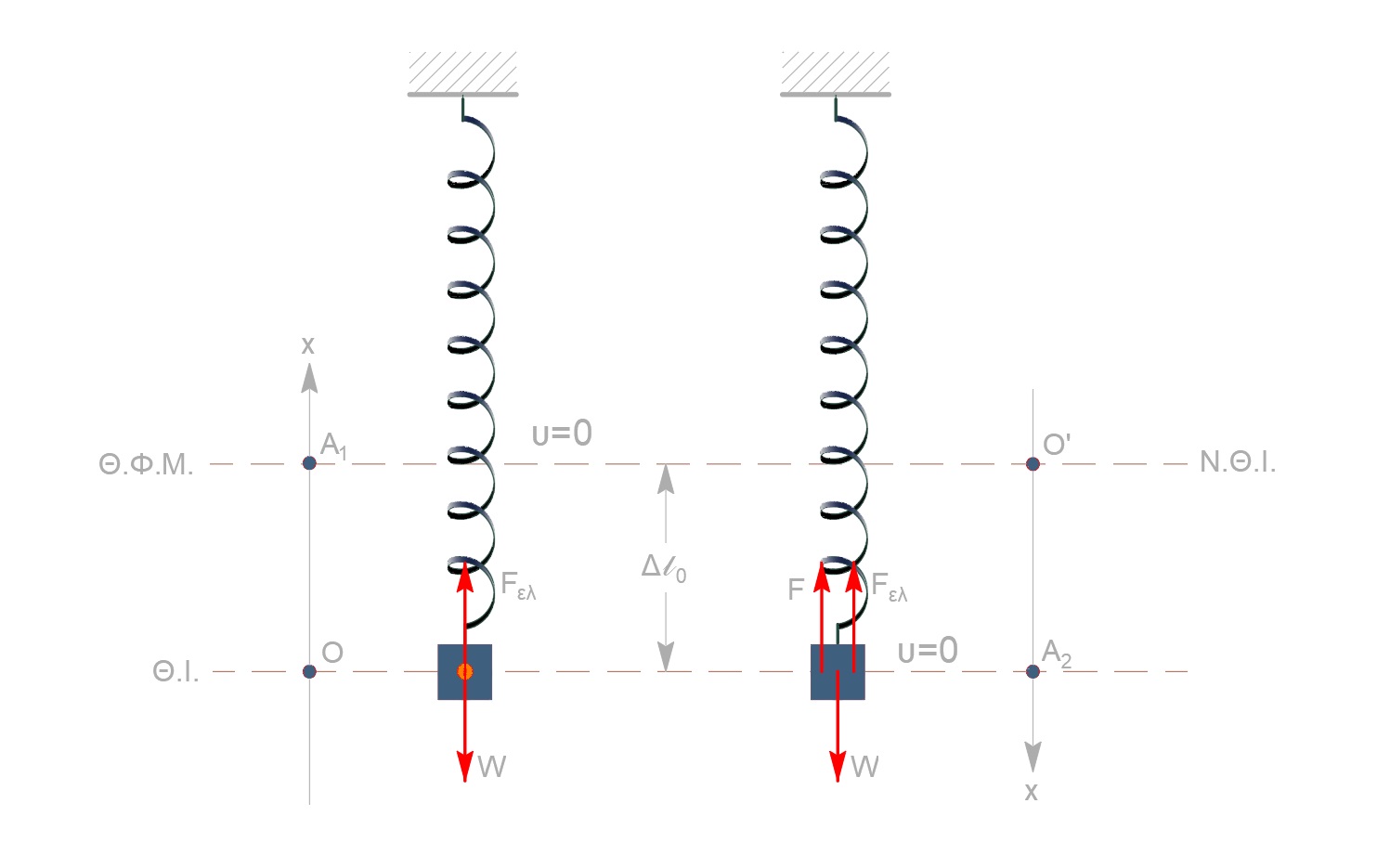
$k-m, \quad A.A.T. \quad πείραμα 1$
\[Θ.Ι._m: \quad ΣF = 0 \Rightarrow F_{ελ} - W = 0 \Rightarrow Δl_o = \frac{mg}{k}\]$Θ.Φ.Μ, \quad υ=0. \quad άρα \quad A_1 = Δl_o$
$F=mg \quad Α.Α.Τ. \quad πείραμα 2$
\[Ν.Θ.Ι: ΣF = 0 \Rightarrow W - F_{ελ} - F = 0 \Rightarrow F_{ελ} = 0 \Rightarrow Δl_1 = 0\]$άρα \quad Ν.Θ.Ι \equiv Θ.Φ.Μ \quad άρα \quad Α_2 = Δl_o$
\[β) \underline {τρόπος}\]$k-m, \quad A.A.T. \quad πείραμα 1$
\[Θ.Φ.Μ._m: \quad ΣF_{max1} = W \Rightarrow m \cdot α_{max1} = m \cdot g \Rightarrow α_{max1} = g\]$F=mg \quad Α.Α.Τ. \quad πείραμα 2$
\[A.Θ.Ι: \quad ΣF_{max2} = F + F_{ελ} - W \Rightarrow m \cdot α_{max2} = F_{ελ}\] \[m \cdot α_{max2} = m \cdot g \Rightarrow α_{max2} = g\] \[ω_1 = ω_2 = \sqrt{\frac{k}{m} }\] \[α_{max1} = α_{max2} \Rightarrow ω_1^2 \cdot A_1 = ω_2^2 \cdot A_2 \Rightarrow A_1 = A_2\] \[γ) \underline {τρόπος}\]$k-m, \quad A.A.T. \quad πείραμα 1$
\[Θ.Ι._m: \quad ΣF = 0 \Rightarrow F_{ελ} - W = 0 \Rightarrow Δl_o = \frac{mg}{k}\]$Θ.Φ.Μ, \quad υ=0. \quad άρα \quad A_1 = Δl_o$
$F=mg \quad Α.Α.Τ. \quad πείραμα 2$
\[Θ.Μ.Κ.Ε \quad ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_{F_{ελ}} + W_F + W_W\]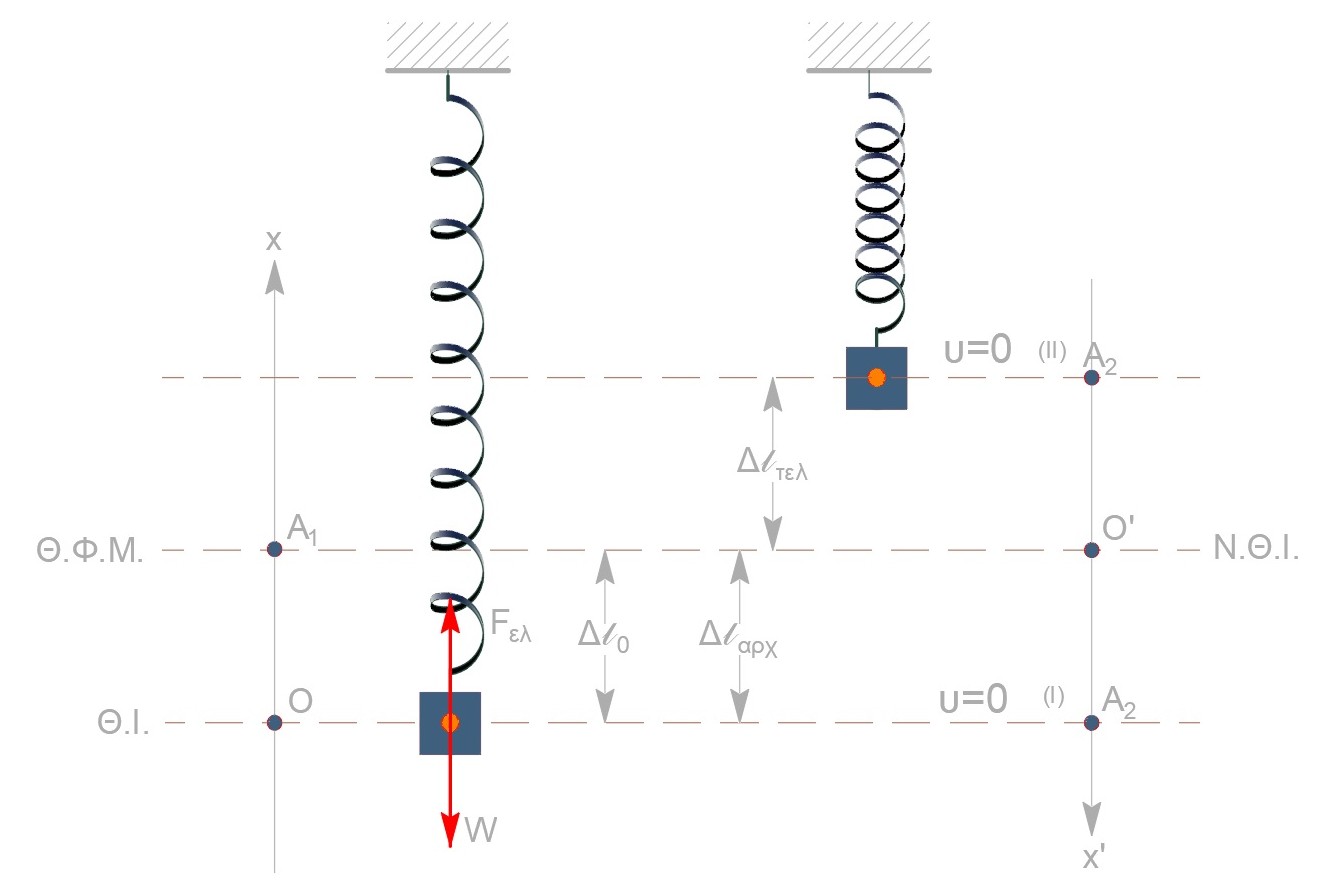
Αφού οι ακραίες θέσεις ισαπέχουν από την $Θ.Φ.Μ$ η θέση φυσικού μήκους είναι και θέση ισορροπίας και ισχύει $Α_2 = Δl_o$
άρα σωστό το \(i\)
Β2 - \((ii)-2-6\)
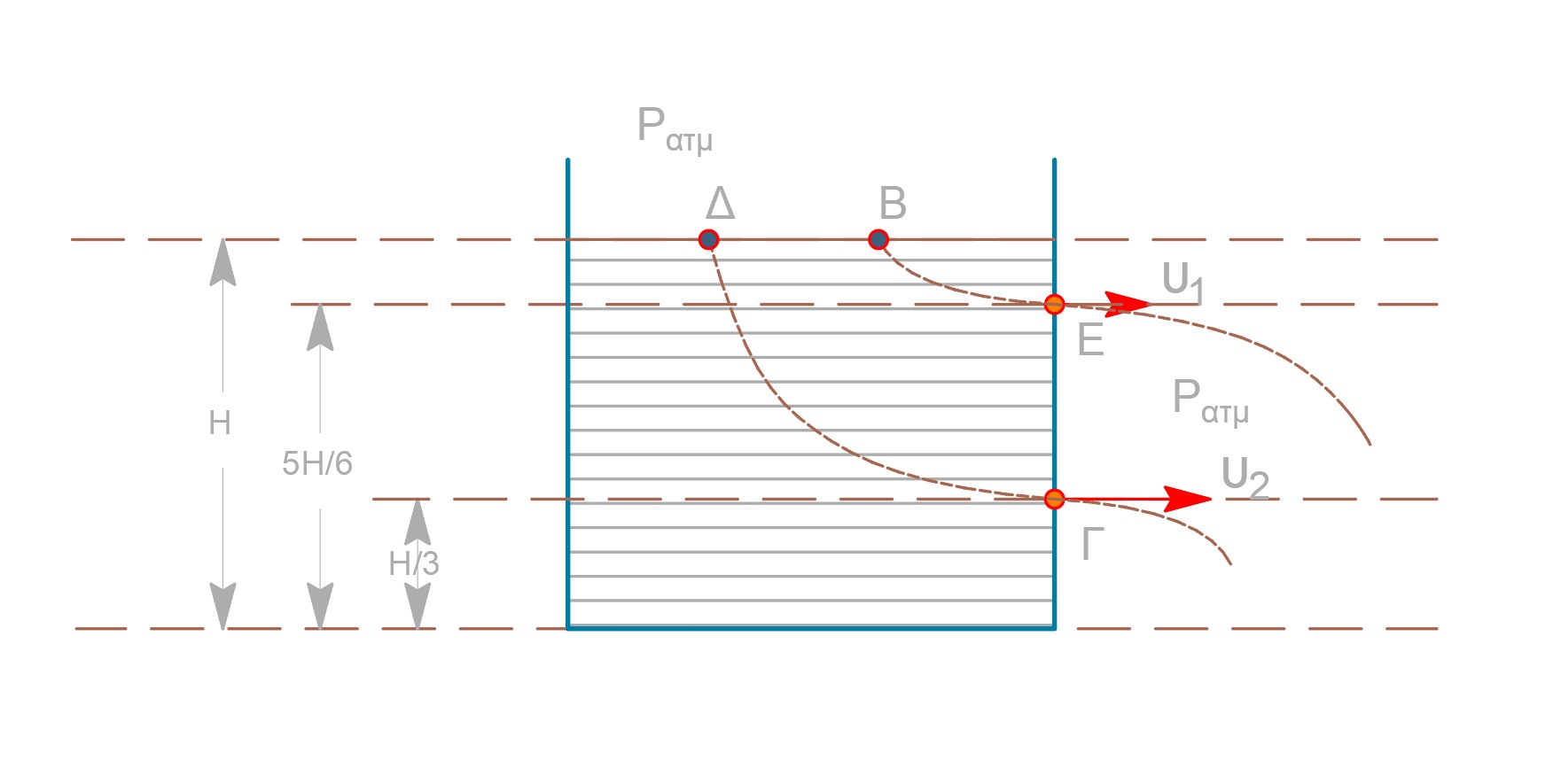
$Bernoulli_{B \rightarrow Ε}$
\[P_{ατμ} + \frac{1}{2} ρ_Β υ^2 + ρ g \frac{H}{6} = P_{ατμ} + \frac{1}{2} ρ υ_1^2 + 0 \Rightarrow υ_1 = \sqrt{\frac{gH}{3}}\] \[A_B υ_Β = Α υ_1 \overset{Α_Β >> Α}{\implies} υ_Β << υ_1\]παρόμοια από το $Δ$ στο $Γ$
\[υ_2 = \sqrt{2g \frac{2H}{3}} \Rightarrow υ_2 = 2\sqrt{\frac{gH}{3}}\]Οπή (1) ανοικτή: $Π_1 = \frac{V}{Δt_1} \Rightarrow Π_1 = Α \cdot \sqrt{\frac{gH}{3} }$
Οπή (1) και (2) ανοικτές: $Π_1 + Π_2 = \frac{V}{Δt_2} \Rightarrow Π_1 + Π_2 = Α \cdot \sqrt{\frac{gH}{3} } + Α \cdot 2 \cdot \sqrt{\frac{gH}{3} } $
\[\frac{Δt_2}{Δt_1} = \frac{Α \cdot \sqrt{\frac{gH}{3} }}{3Α \cdot \sqrt{\frac{gH}{3} }} \Rightarrow \frac{Δt_2}{Δt_1} = \frac{1}{3}\]άρα σωστό το \(ii\)
Β3 - \((iii)-2-7\)
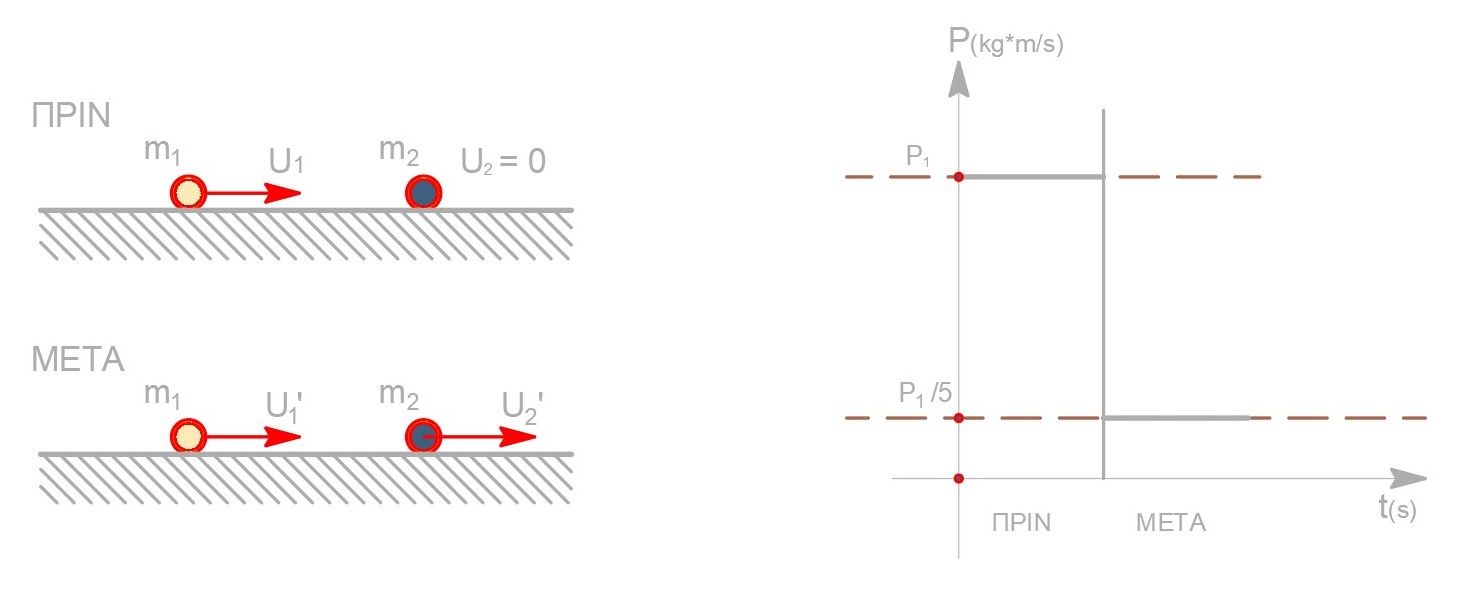
Η κινητική ενέργεια που έχασε το $m_1$ μεταβιβάστηκε στο $m_2$.
\[ΔΚ_1^{απώλεια} = Κ_1 - Κ_1' = \frac{1}{2} m_1 υ_1^2 - \frac{1}{2} m_1 \frac{υ_1^2}{25} = \frac{24}{25} K_1\] \[Π_{1\rightarrow2}\% = \frac{ΔΚ_1^{απώλεια}}{K_1} 100 \% = \frac{24}{25} 100 \% = 96 \%\] \[γ) \underline {τρόπος}\] \[p_1' = \frac{p_1}{5} \Rightarrow m_1 υ_1' = \frac{m_1 υ_1}{5} \Rightarrow υ_1' = \frac{υ_1}{5}\]Α.Δ.Ο και Δ.Κ.Ε.
\[υ_1' = \frac{m_1 - m_2}{m_1 + m_2} υ_1 \Rightarrow \frac{υ_1}{5} = \frac{m_1 - m_2}{m_1 + m_2} υ_1 \Rightarrow 2 m_1 = 3 m_2\] \[υ_2' = \frac{2m_1}{m_1 + m_2} υ_1 \Rightarrow υ_2' = \frac{6}{5} υ_1\] \[Π_{1\rightarrow2}\% = \frac{K_2'}{K_1} 100 \% = \frac{ \frac{1}{2} m_2 υ_2'^2}{\frac{1}{2} m_1 υ_1^2 } 100 \% = 96 \%\] \[δ) \underline {τρόπος}\] \[Α.Δ.Ο. \quad \vec{p}_{πριν} = \vec{p}_{μετά} \Rightarrow p_1 + 0 = \frac{p_1}{5} + p_2' \Rightarrow p_2' = \frac{4}{5} p_1\] \[K = \frac{1}{2} m υ^2, \quad p=mυ, \quad K = \frac{1}{2} m \frac{p^2}{2m} \Rightarrow K = \frac{p^2}{2m}\] \[K_1' = \frac{(\frac{p_1}{5})^2}{2m_1}, \quad K_2' = \frac{(\frac{4p_1}{5})^2}{2m_2} = \frac{16 p_1^2}{50 m_2}\] \[Δ.Κ.Ε. \quad K_1 + 0 = K_1' + K_2' \Rightarrow \frac{p_1^2}{2m_1} = \frac{1}{25} \cdot \frac{p_1^2}{2m_1} + \frac{16}{25} \cdot \frac{p_1^2}{2m_2}\] \[2 \cdot m_1 = 3 \cdot m_2\] \[Π_{1\rightarrow2}\% = \frac{K_2'}{K_1} 100 \% = \frac{\frac{16 p_1^2}{50 m_2}}{ \frac{p_1^2}{2 m_1}} 100 \% = 96 \%\]άρα σωστό το \(iii\)
Θέμα Γ
Γ1-\((4)\)
\[I = \frac{E}{R_{ΚΛ} + r} \Rightarrow I = 3A\]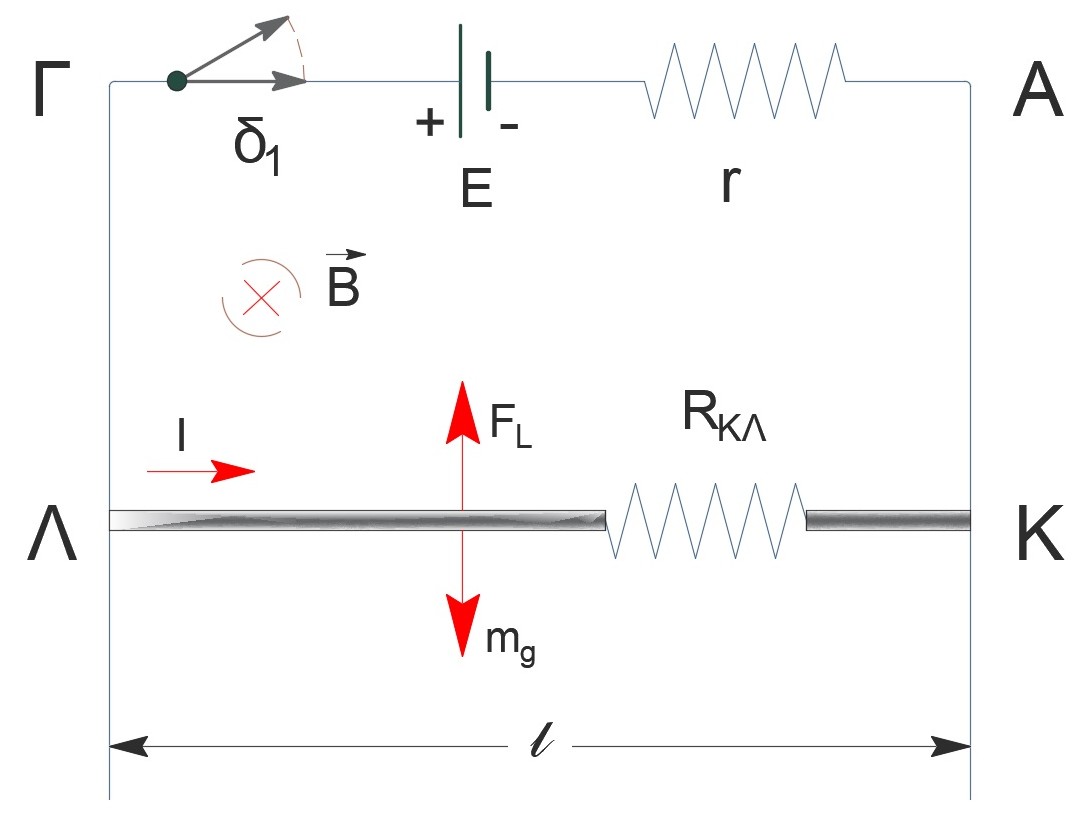
Γ2-\((9)\)
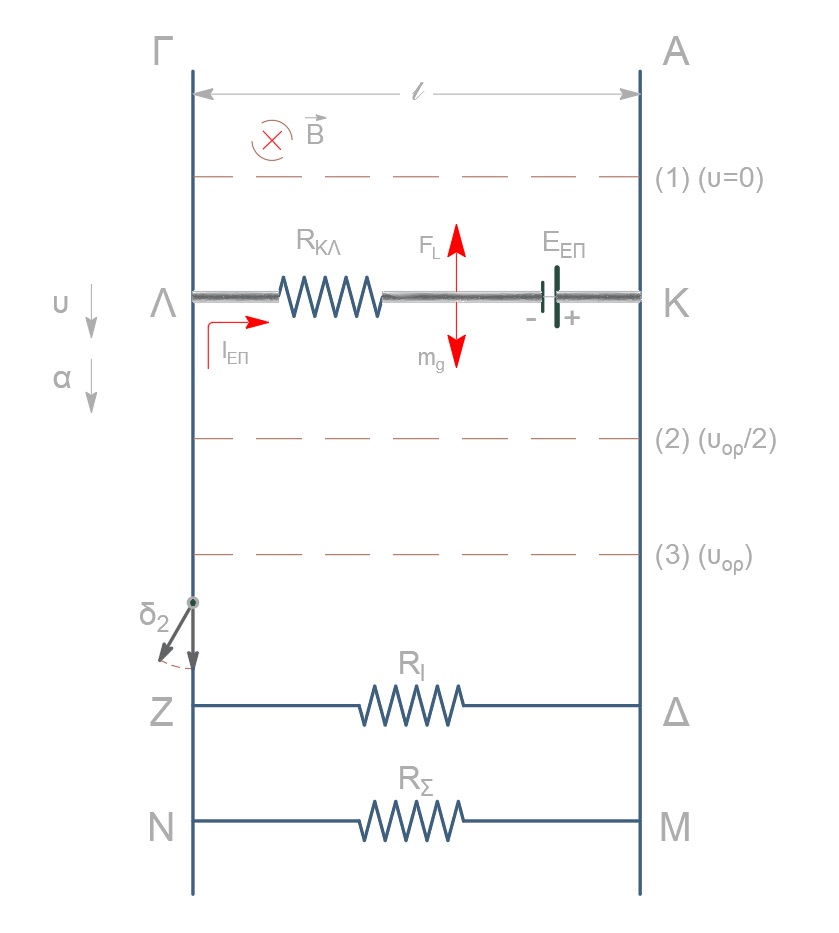
Ο αγωγός $ΚΛ$ στη θέση $(1)$ είναι ακίνητος. Εξαιτίας της δύναμης του βάρους κινείται κατακόρυφα κάθετα στο μαγνητικό πεδίο, άρα αυξάνεται η ταχύτητά του. Εμφανίζεται στα άκρα του αγωγού ηλεκτρεγερτική δύναμη από επαγωγή $Ε_{επ} = Βυl$ με πολικότητα, σύμφωνα με τον κανόνα του $Lenz$, όπως φαίνεται στο σχήμα, οπότε το κύκλωμα διαρρέεται από επαγωγικό ρεύμα που συνεχώς αυξάνεται. Στον αγωγό που διαρρέεται από επαγωγικό ρεύμα εμφανίζεται δύναμη $Laplace$
\[F_L = BI_{επ}l = \frac{B E_{επ} l}{R_{ολ}} = \frac{B^2l^2υ}{R_{ολ}}\]με κατεύθυνση που φαίνεται στο σχήμα. Το μέτρο της δύναμης $Laplace$ αυξάνεται διότι η ταχύτητα αυξάνεται. Η συνισταμένη δύναμη (βάρος + $Laplace$) ελαττώνεται οπότε η κίνηση του αγωγού είναι επιταχυνόμενη με επιτάχυνση που συνεχώς ελαττώνεται.
\[ΜΝ, κανονική \quad λειτουργία: \quad P_K = \frac{V_K^2}{R_Σ} \Rightarrow R_Σ = 6Ω\] \[\frac{1}{R_{1,Σ}} = \frac{1}{R_1} + \frac{1}{R_Σ} \Rightarrow R_{1,Σ} = 2Ω\] \[Ε_{ΕΠ} = |-\frac{ΔΦ}{Δt}| = B \cdot \frac{Δx}{Δt} \cdot l = B υ l\] \[ΣF = m α \Rightarrow mg - F_L = m α \Rightarrow mg - B I_{επ}l = m α\] \[Ι_{επ} = \frac{E_{επ}}{R_{ολ}} = \frac{Bυl}{R_{ΚΛ}+R_{1,Σ}}\] \[mg - \frac{B^2\cdot l^2 \cdot υ}{R_{ΚΛ}+R_{1,Σ}} = m α \Rightarrow α=10 - \frac{5}{6}υ \quad (S.I.)\] \[υ = υ_{ορ} \Rightarrow α=0 \Rightarrow 0 = 10 - \frac{5}{6}υ_{ορ} \Rightarrow υ_{ορ} = 12 \frac{m}{s}\]Γ3-\((6)\)
\[α) \underline {τρόπος}\] \[KΛ, \quad θέση (2) \quad υ = \frac{υ_{ορ}}{2} \Rightarrow υ = 6\frac{m}{s}\] \[α=10 - \frac{5}{6}υ \Rightarrow α = 5 \frac{m}{s^2}\] \[\frac{d \vec{p}}{dt} = Σ \vec{F} \Rightarrow \frac{d \vec{p}}{dt} = m \vec{α} \Rightarrow |\frac{d \vec{p}}{dt}| = 1.5 kg \frac{m}{s^2}\] \[β) \underline {τρόπος}\]Τη στιγμή όπου $υ=\frac{υ_{ορ}}{2} = 6 \frac{m}{s}$
\[I'=\frac{Bvl}{R_{ολ}} \Rightarrow I' =\frac{Bvl}{R_{ΚΛ}+R_{1,Σ}} \Rightarrow I' = 1,5A\] \[\frac{dp}{dt}=ΣF=mg-F_L=mg-BI'l=1,5kg\frac{m}{s^2}\]$\frac{d \vec{p}}{dt}$ με φορά προς τα κάτω.
Γ4-\((6)\)
\[Ε_{επ} = Β υ_{ορ} l \Rightarrow E_{επ} = 12 V\] \[I_{επ} = \frac{E_{επ}}{R_{ΚΛ} + R_{1,Σ}} \Rightarrow I_{επ} = 3Α\] \[α) \underline {τρόπος}\] \[V_{MN} = I_{επ} R_{1,Σ} \Rightarrow V_{ΜΝ} = 6 V \Rightarrow V_{ΜΝ} = V_K\]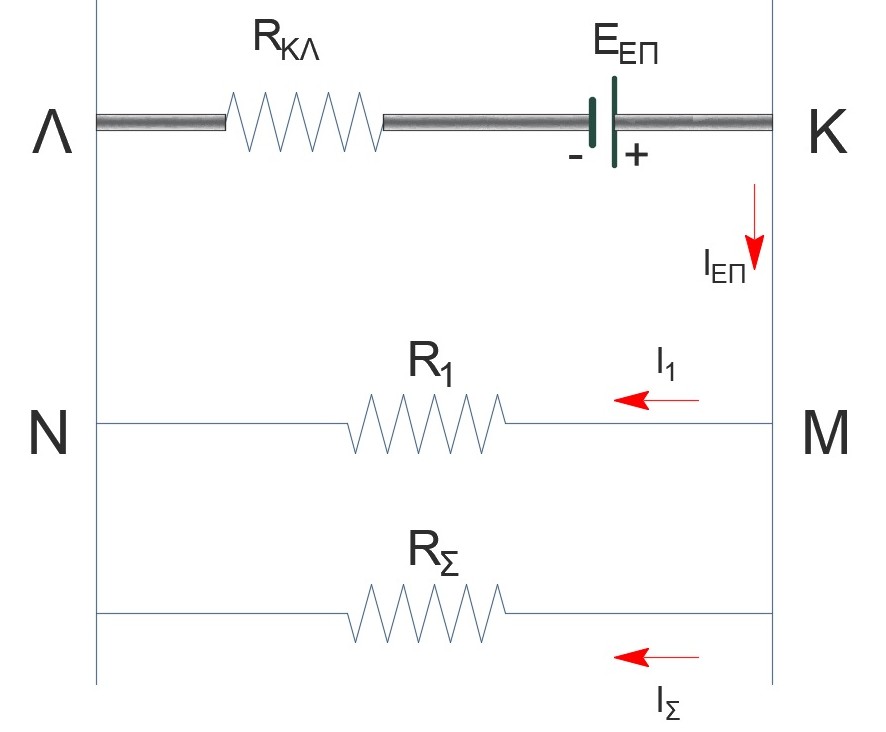
άρα λειτουργεί κανονικά η συσκευή.
Θέμα Δ
Δ1-\((4)\)
\[α) \underline {τρόπος}\]$M_ρ - m$ ισορροπία:
\[Στ_{(Γ)} = 0 \Rightarrow τ_Ν + τ_W - τ_{T_1} = 0\] \[N \cdot \frac{l}{2} συνφ + W \cdot \frac{l}{2} συνφ - Τ_1 \frac{l}{2} ημφ = 0 \Rightarrow N = 4N\]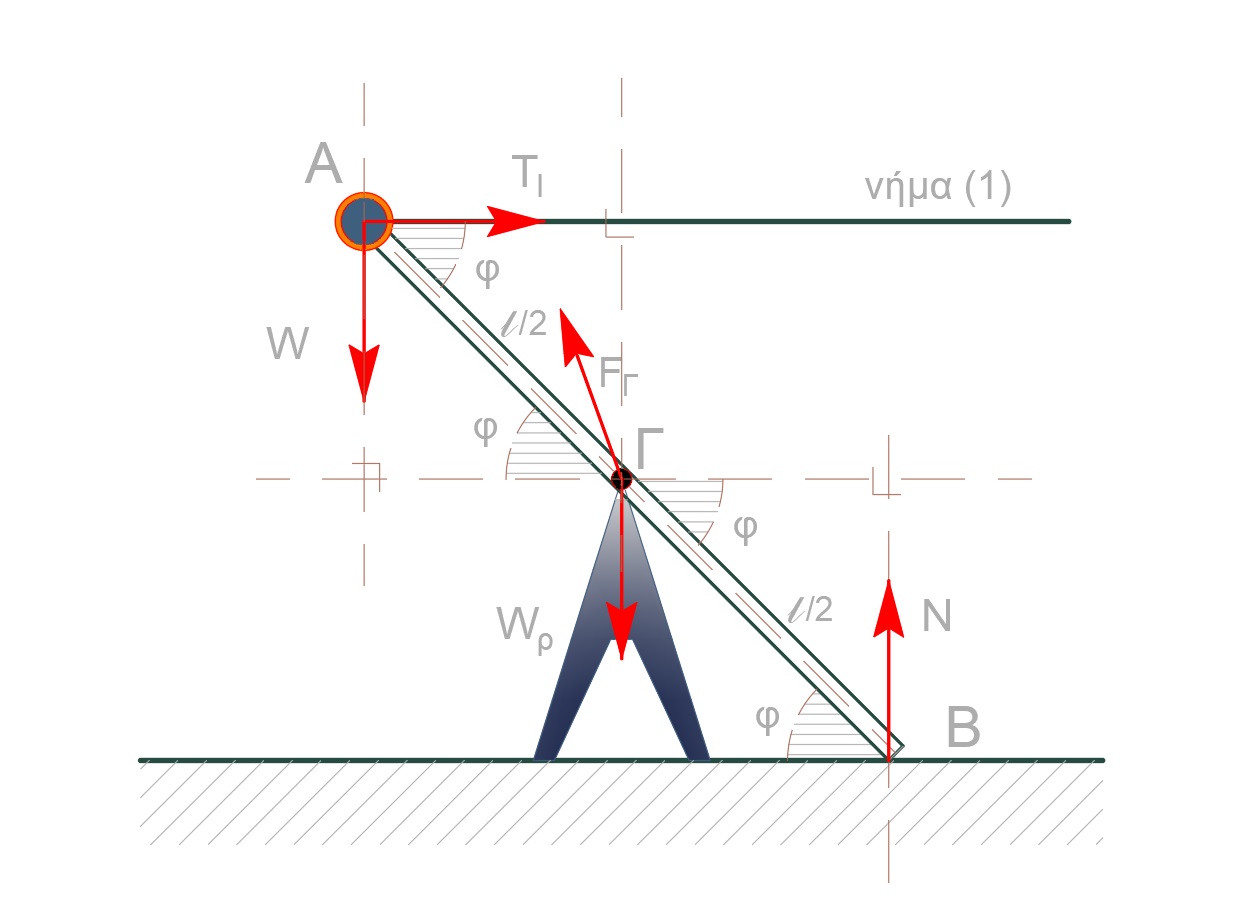
και μετά τις πράξεις $Ν = 4Ν$.
\[γ) \underline {τρόπος}\]Έστω $F_{ρσ}$ η δύναμη που ασκεί η ράβδος στο σφαιρίδιο και $F_{σρ}$ η δύναμη που ασκεί το σφαιρίδιο στη ράβδο. Εξαιτίας του τρίτου νόμου του Νεύτωνα οι δυνάμεις θα έχουν ίσα μέτρα.
\[m \quad ισορροπία \quad ΣF_x = 0 \Rightarrow F_{ρσx} = T_1 \Rightarrow F_{ρσx} = 10.5N\] \[m \quad ισορροπία \quad ΣF_y = 0 \Rightarrow F_{ρσy} = W \Rightarrow F_{ρσy} = 10N\]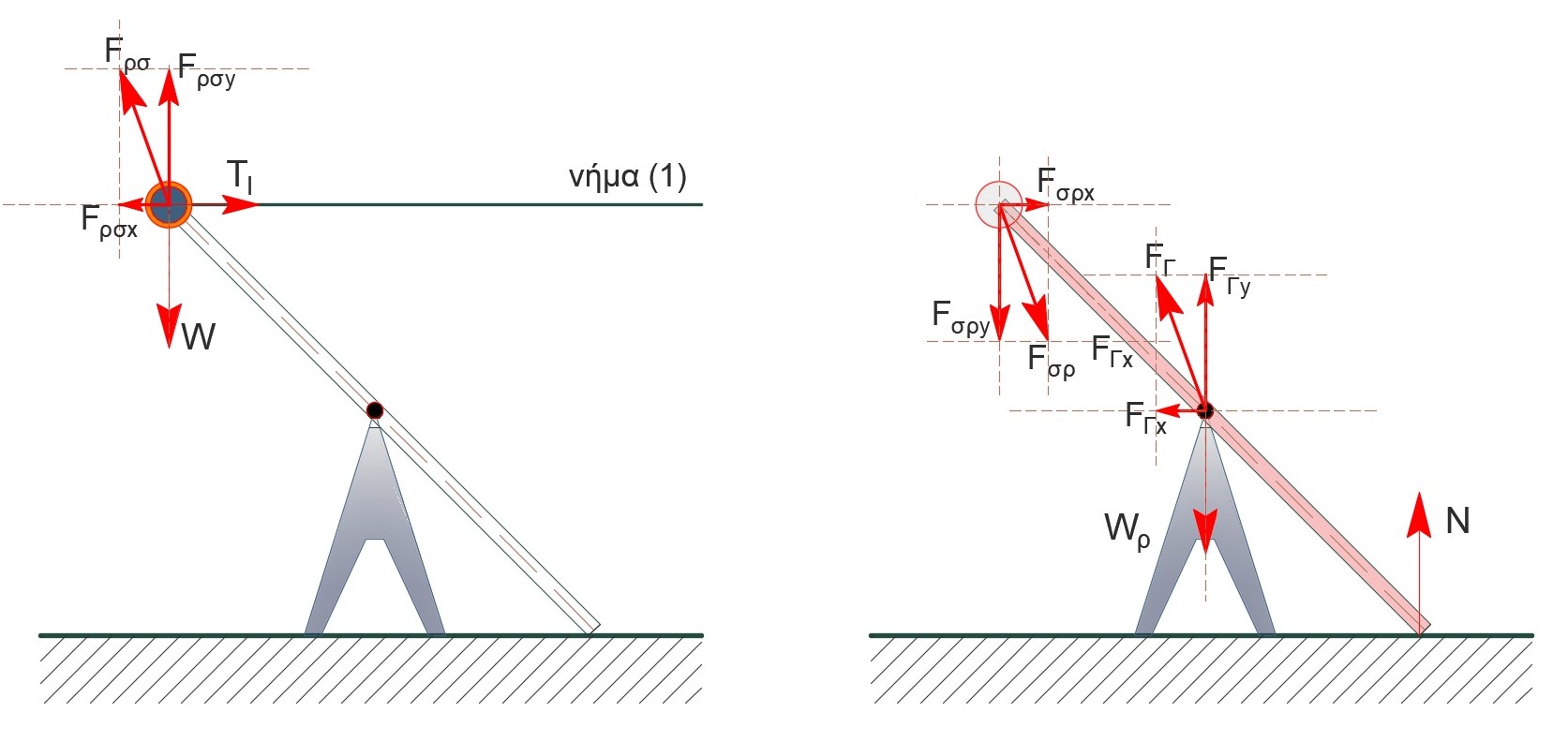
και μετά τις πράξεις $F_{Γ_y} = 36Ν$ και $Ν=4Ν$.
Δ2-\((6)\)
\[α) \underline {τρόπος}\] \[I_{ολ}=I_{ρ}+I_{σφ}=\frac{1}{12}M_ρl^2+m\left(\frac{l}{2}\right)^2 \Rightarrow I_{ολ}=2kg\cdot m^2\] \[m-M_ρ: \quad Στ_{(Γ)} = Ι \cdot α_{γων}\] \[W \cdot \frac{l}{2} συνφ = Ι_{ολ} \cdot α_{γων} \Rightarrow α_{γων} = 3 \frac{rad}{s^2}\] \[\frac{dL_ρ}{dt}=I_ρ\cdot α_{γων}=3kg\cdot m^2/s^2\]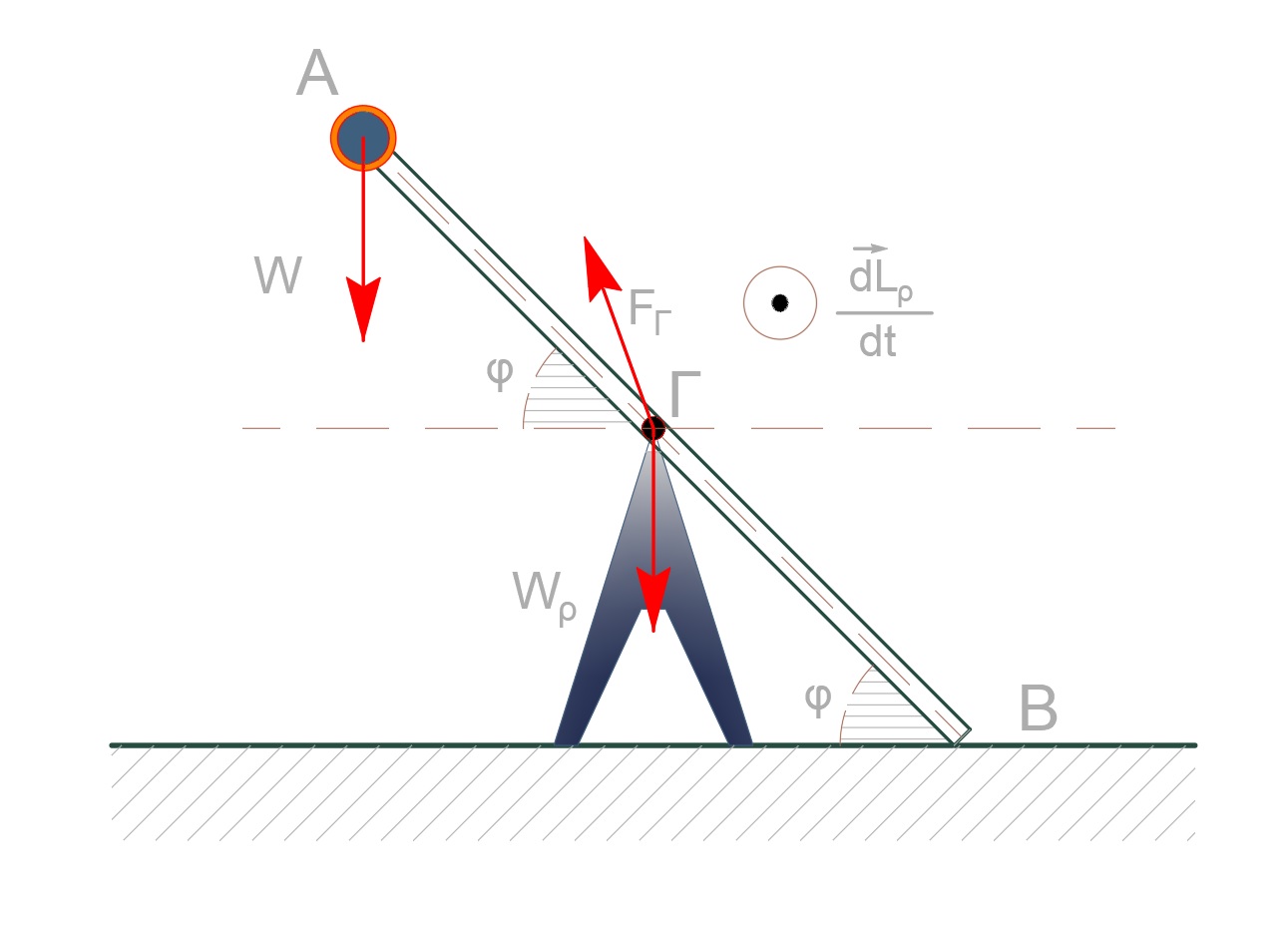
Έστω $F$ η δύναμη που δέχεται το σφαιρίδιο από την ράβδο με συνιστώσες $F_x$ και $F_y$. και $F’$ η δύναμη που ασκεί το σφαιρίδιο στην ράβδο. Ισχύει $F=F’$ εξαιτίας του τρίτου νόμου του Νεύτωνα.
\[m: \quad F_{επιτ} = m \cdot α_{επιτ} \Rightarrow W_x - F_y = m \cdot α_{επιτ}\] \[mg συνφ - F_y = m \cdot α_{γων} \cdot \frac{l}{2}\] \[τ_{F_y'} = \frac{dL_ρ}{dt} \Rightarrow F_y \cdot \frac{l}{2} = \frac{1}{12} M_ρ \cdot l^2 \cdot α_{γων}\] \[α_{γων} = \frac{6F_y}{lM_ρ}\] \[F_y = \frac{mg συνφ}{1+ \frac{6ml}{2M_ρ}} \Rightarrow F_y = 3N\] \[\frac{dL_ρ}{dt} = τ_{F_y} = F_y \cdot \frac{l}{2} \Rightarrow \frac{dL_ρ}{dt} = 3 \frac{kg m^2}{s^2}\]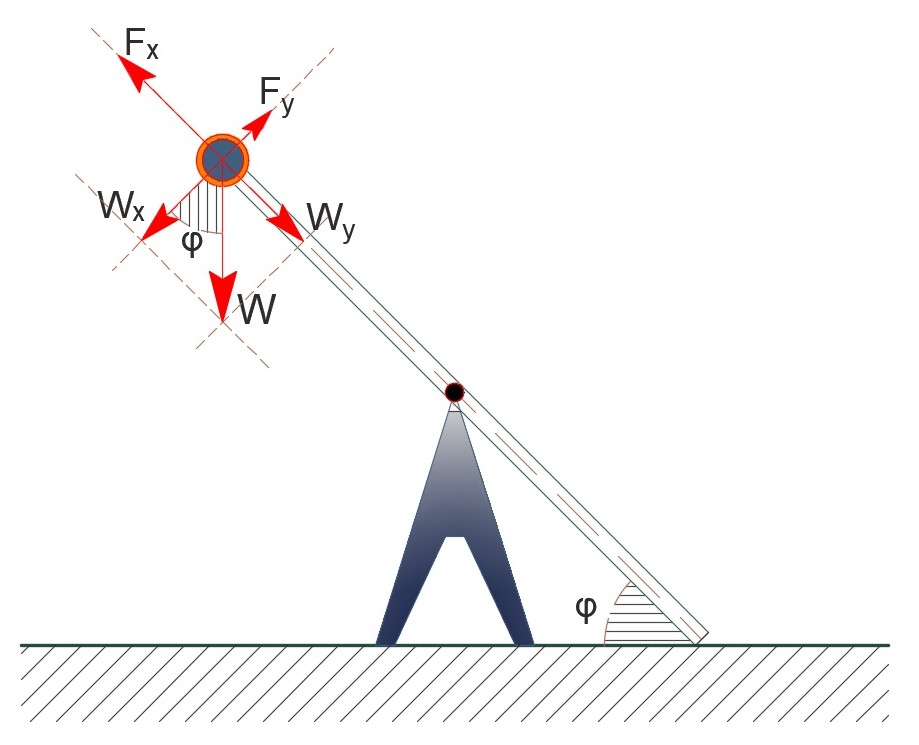
Δ3-\((5)\)
\[α) \underline {τρόπος}\] \[Α.Δ.Μ.Ε. \quad m-M_ρ \quad (I \rightarrow II): E_I^{ΜΗΧ} = E_{ΙI}^{ΜΗΧ}\] \[K_I + U_I = K_{II} + U_{II} \Rightarrow 0 + mglημφ + U_{M_ρ}^Ι = \frac{1}{2}I ω^2 + 0 + U_{M_ρ}^{ΙΙ}\]και μετά τις πράξεις $ω = 4 \frac{rad}{s}$
\[β) \underline {τρόπος}\] \[Θ.Μ.Κ.Ε._{Ι \rightarrow II} \quad ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_B\] \[\frac{1}{2} I_{ολ} ω^2 = m g l ημφ \Rightarrow ω = 4 \frac{rad}{s}\] \[γ) \underline {τρόπος}\]Υπολογισμός της κατακόρυφης απόστασης $(Ι \rightarrow II)$ από το σχήμα
\[d = l \cdot ημφ \Rightarrow d = 1.6m \quad d = \frac{l}{2} ημφ + 2R \Rightarrow d = 1.6m\]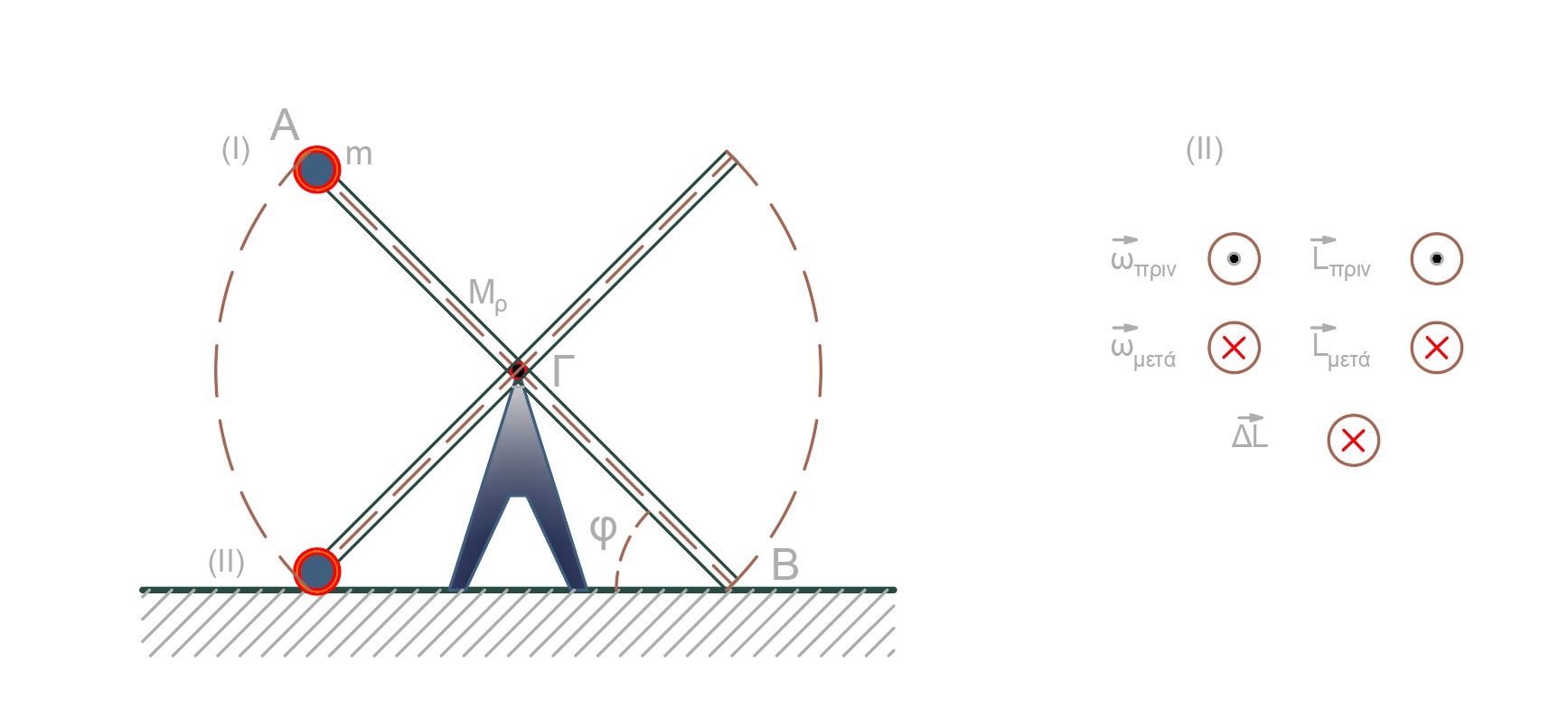
άρα το μέτρο του $Δ\vec{L}$ είναι $| Δ\vec{L} | = 12 kg \frac{m^2}{s}$ και η φορά φαίνεται στο σχήμα.
Δ4-\((4)\)
\[α) \underline {τρόπος}\]Νήμα αβαρές και μη εκτατό $F=T_2=T_2’=12N$
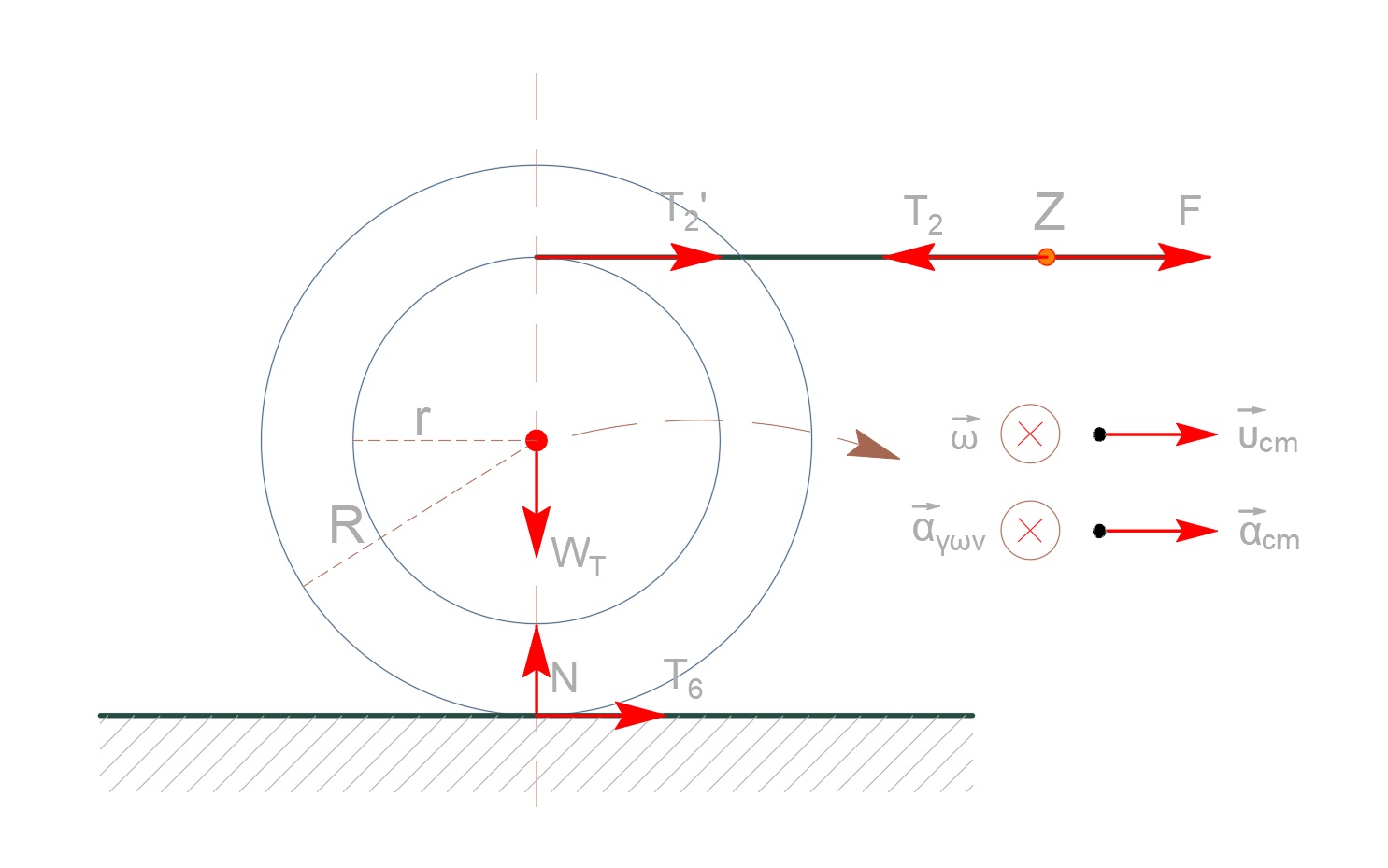
$M_τ$ μεταφορική κίνηση
\[ΣF = M_τ α_{cm} \Rightarrow T_2' + T_{στ} = M_τ \cdot α_{cm}\] \[Κ.Χ.Ο. \quad Δx_{cm} = Δθ \cdot R \Rightarrow υ_{cm} = ω R \Rightarrow α_{cm} = α_{γων} R\]$M_τ$ στροφική κίνηση
\[Στ = Ι_τ α_{γων} \Rightarrow T_2' \cdot r - T_{στ} \cdot R = I_τ \cdot α_{γων}\]και μετά τις πράξεις $α_{cm} = 2 \frac{m}{s^2}$
\[β) \underline {τρόπος}\]Α, σημείο επαφής τροχαλίας δαπέδου
\[Ι_Α = Ι_{cm} + M_τ \cdot R^2 \Rightarrow I_A = \frac{3}{2} M_τ \cdot R^2\] \[Στ_{(Α)} = Ι_Α α_{γων} \Rightarrow F\cdot (R+r) = \frac{3}{2} M_τ \cdot R^2 \cdot α_{γων} \Rightarrow α_{γων} = 5\frac{rad}{s^2}\] \[α_{cm} = α_{γων} \cdot R^2 \Rightarrow α_{cm} = 2 \frac{m}{s^2}\]Δ5-\((6)\)
\[α) \underline {τρόπος}\]Από $t_o = 0$ έως $t_1 = 2 s$:
\[Δx_Z = Δx_{cm} + Δθ \cdot r = Δθ \cdot R + Δθ \cdot r = Δθ \cdot (R+r) = \frac{Δx_{cm}}{R}(R+r)\] \[Δx_{cm} = \frac{1}{2} α_{cm} t_1^2 \Rightarrow Δx_{cm} = 4m\] \[W_F = F \cdot Δx_Z \cdot συν0 \Rightarrow W_F = 84J\] \[β) \underline {τρόπος}\] \[W_F^{μεταφορική} = F \cdot Δx_{cm} = F \cdot \frac{1}{2} α_{cm} t_1^2 = 48 J\] \[W_{τ_F}^{στροφική} = τ_F \cdot θ = F \cdot r \cdot \frac{1}{2} α_{γων} t_1^2 = 36 J\] \[W_F = W_F^{μεταφορική} + W_{τ_F}^{στροφική} \Rightarrow W_F = 84 J\] \[γ) \underline {τρόπος}\] \[Δx_Z = Δx_{cm} + Δθ \cdot r \Rightarrow α_Ζ = α_{cm} + α_{γων} r\] \[α_Ζ = α_{cm} + \frac{α_{cm}}{R} \cdot r \Rightarrow α_Ζ = α_{cm}(1+ \frac{r}{R} ) \Rightarrow α_Ζ = \frac{7}{2} \frac{m}{s^2}\] \[W_F = F \cdot Δx_Z \cdot συνφ \Rightarrow W_F = 84 J\] \[δ) \underline {τρόπος}\] \[ω = α_{γων} \cdot t_1 \Rightarrow ω = \frac{α_{cm}}{R} \cdot t_1 \Rightarrow ω = 10 \frac{rad}{s}\] \[υ_{cm} = ω \cdot R \Rightarrow υ_{cm} = 4 \frac{m}{s}\] \[Θ.Μ.Κ.Ε._{t_o \rightarrow t_1} ΔΚ = ΣW \Rightarrow K_1 - K_o = W_F\] \[W_F = \frac{1}{2} I_{ολ} ω^2 + \frac{1}{2} Μ_τ υ_{cm}^2 \Rightarrow W_F = 84 J\]Μπορείτε να εκτυπώσετε τα θέματα και τις λύσεις σε μορφή pdf
blog comments powered by Disqus