Ευθύγραμμος ρευματοφόρος αγωγός Απόδειξη της σχέσης 4.2 του σχολικού βιβλίου
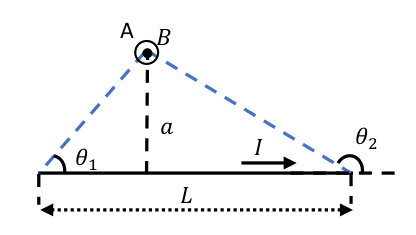
Έστω το ευθύγραμμο σύρμα του παραπάνω σχήματος μήκους \(L\) που διαρρέεται από ρεύμα έντασης \(Ι\). θέλουμε να υπολογίσουμε το μαγνητικό πεδίο που δημιουργεί ο αγωγός στο σημείο \(Α\), που απέχει απόσταση \(α\) από τον αγωγό.
Θεωρούμε το παρακάτω σχήμα όπου παίρνουμε ως αρχή των συντεταγμένων \(Ο\) το κοντινότερο σημείο του αγωγού στο σημείο \(Α\) και τοποθετούμε τον άξονα \(𝑥\) επάνω στον αγωγό, με την ίδια φορά όπως και αυτή του ρεύματος.
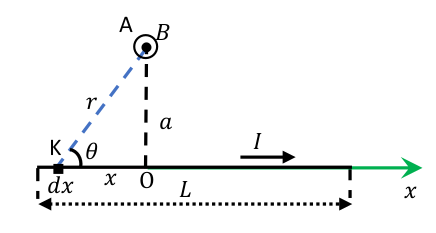
Χωρίζουμε τον αγωγό σε πολύ μικρά τμήματα. Έστω ένα τέτοιο τμήμα μήκους \(𝑑𝑥\) στο σημείο \(Κ\) με συντεταγμένη \(𝑥\) (αρνητική για τα σημεία αριστερά του \(Ο\)) και που απέχει απόσταση \(𝑟\) από το σημείο \(Α\). Το μικρό αυτό τμήμα δημιουργεί στο σημείο \(Α\) μαγνητικό πεδίο μέτρου
\[dB = \frac{μ_ο I}{4π} \cdot \frac{dx}{r^2} \cdot ημθ\]Το συνολικό πεδίο θα είναι ίσο με
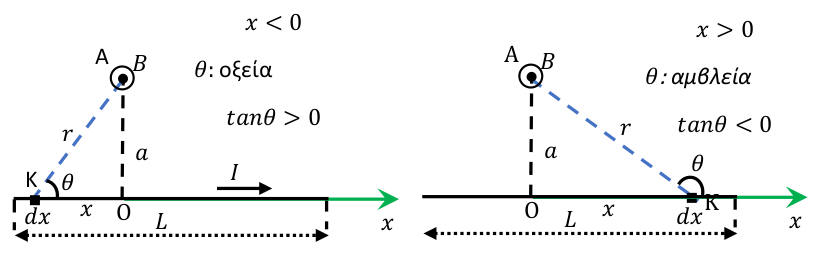
\[B = \frac{μ_ο I}{4π} \int_{x_1}^{x_2} \frac{dx}{r^2} \cdot ημθ\]όπου τα \(𝑥_1\) και \(𝑥_2\) είναι οι συντεταγμένες των άκρων του αγωγού. Τα εκφράζουμε όλα συναρτήσει της γωνίας \(𝜃\). Το \(𝑥\) μπορούμε να το εκφράσουμε με την βοήθεια της απλής τριγωνομετρίας συναρτήσει της εφαπτομένης αλλά το πρόσημο χρειάζεται προσοχή επειδή στα αριστερά του \(Ο\) ισχύει \(𝑥 < 0\) ενώ αντιθέτως \(εφ𝜃 > 0\) επειδή η \(𝜃\) είναι οξεία. Έτσι πρέπει να γράψουμε
\[εφθ = -\frac{α}{x}\]Στα δεξιά του \(Ο\) όπου \(𝑥 > 0\) και πάλι ο τύπος δίνει το σωστό αποτέλεσμα επειδή η \(𝜃\) είναι αμβλεία και \(εφ𝜃 < 0\).
Λύνοντας ως προς \(𝑥\) και διαφορίζοντας έχουμε
\[x = -\frac{α}{εφθ} \Rightarrow dx = \frac{α dθ}{ημ^2θ}\]Το \(r\) το εκφράζουμε με τη βοήθεια της τριγωνομετρίας συναρτήσει του ημιτόνου.
\[ημθ = \frac{α}{r} \Rightarrow r = \frac{α}{ημθ}\]Μαζεύοντας όλα τα παραπάνω, η υπο-ολοκλήρωση ποσότητα ισούται με
\[\frac{dx}{r^2} \cdot ημθ = \frac{\frac{α dθ}{ημ^2θ}}{\frac{α^2}{ημ^2θ}} \cdot ημθ = \frac{1}{α} ημθ\]Το ολοκλήρωμα τώρα υπολογίζεται εύκολα
\[B = \frac{μ_ο I}{4πα} \int_{θ_1}^{θ_2} ημθ \cdot dθ = \frac{μ_ο I}{4πα} \cdot [-συνθ]_{θ_1}^{θ_2}\]και μετά τις πράξεις
\[Β = \frac{μ_ο I}{4πα} (συνθ_1 - συνθ_2)\]όπου οι \(θ_1\) και \(θ_2\) φαίνονται στο αρχικό σχήμα.
blog comments powered by Disqus