Σώμα, απλή και διπλή τροχαλία

Διπλή τροχαλία \(Σ_1\) συνολικής μάζας \(Μ = \frac{10}{9} kg\) αποτελείται από δύο ομογενείς, συγκολλημένους, ομοαξονικούς δίσκους, με ακτίνες \(r = \frac{1}{10} m\) και \(R = 2r\). Στην περιφέρεια του δίσκου με ακτίνα \(r\) έχουμε τυλίξει το ένα άκρο αβαρούς και μη εκτατού νήματος το άλλο άκρο του οποίου συνδέεται μέσω απλής αβαρούς τροχαλίας ακτίνας \(r'= \frac{25}{19} \cdot r\) με σώμα \(Σ_2\) μάζας \(m=10 kg\) όπως φαίνεται στο σχήμα.

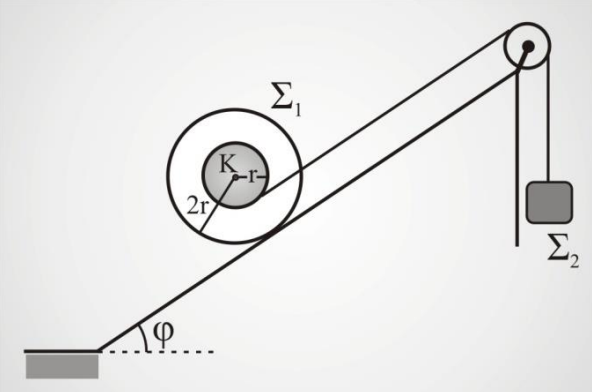
Την χρονική στιγμή \(t=0\) αφήνεται το σύστημα των τριών σωμάτων ελεύθερο να κινηθεί. Εάν η διπλή τροχαλία κυλίεται χωρίς να ολισθαίνει να βρεθεί:

1) το μέτρο της επιτάχυνσης με την οποία κατέρχεται το σώμα \(Σ_2\).

2) η γωνιακή επιτάχυνση (μέτρο, κατεύθυνση) της διπλής τροχαλίας \(Σ_1\).

3) ο ρυθμός μεταβολής στροφορμής της διπλής τροχαλίας \(Σ_1\).

Την χρονική στιγμή \(t_1\) που το σώμα \(Σ_2\) μάζας \(m\) έχει κατέβει κατά \(h = 0.25m\) από την αρχική του θέση κόβουμε το νήμα που συνδέει τις δύο τροχαλίες.

4) Ποια είναι η στροφορμή του δίσκου ακτίνας \(r\) την χρονική στιγμή \(t_1\) αν γνωρίζουμε ότι η ροπή αδράνειάς του είναι \(Ι_1 = 0.1 kg m^2\).

5) Να βρεθεί ο συνολικός αριθμός των περιστροφών που εκτελεί η απλή τροχαλία έως τη χρονική στιγμή που ακινητοποιείται στιγμιαία η διπλή τροχαλία.

Δίνεται η επιτάχυνση της βαρύτητας \(g=10 \frac{m}{s^2}\), η ροπή αδράνειας της διπλής τροχαλίας \(I=0.3 kg m^2\) και η γωνία κλίσης του κεκλιμένου επιπέδου \(φ = 30^ο\).