Τριβή ολίσθησης και στερεό (study4exams) όταν το έργο της τριβής δεν μετατρέπεται όλο σε θερμότητα
Ένας συμπαγής, ομογενής κύλινδρος έχει μάζα \(m = 2 kg\), ακτίνα \(R = 0.2 m\) και κινείται σε οριζόντιο δάπεδο υπό την επίδραση οριζόντιας δύναμης \(F\) η οποία ασκείται στο κέντρο του \(Κ\). Η γωνιακή ταχύτητα του κυλίνδρου και η ταχύτητα του κέντρου μάζας του, σε σχέση με το χρόνο που ασκείται η δύναμη, αποτυπώνονται στα διαγράμματα του σχήματος.
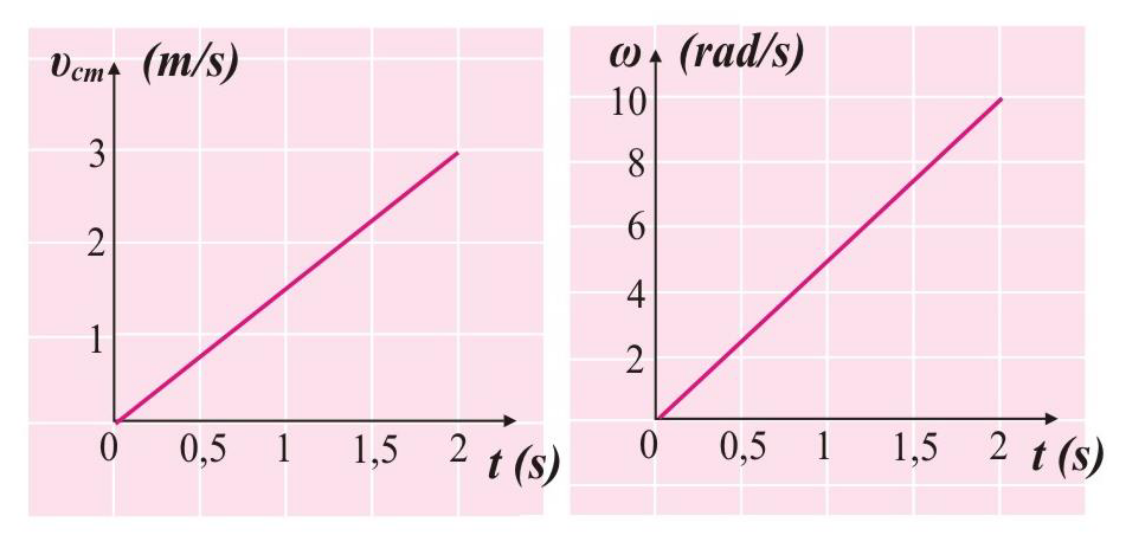
\(Γ_1\) Να υπολογίσετε τη γωνιακή επιτάχυνση \(α_{γων}\) του κυλίνδρου, την επιτάχυνση \(α_{cm}\) του κέντρου μάζας και να προσδιορίσετε την κίνηση που εκτελεί ο κύλινδρος συνολικά.
\(Γ_2\) Να υπολογίσετε το συντελεστή τριβής μεταξύ δίσκου και δαπέδου.
Από τη χρονική στιγμή \(t_0 = 0\) ως τη στιγμή \(t_1 = 2 s\).
\(Γ_3\) Να υπολογίσετε το έργο της δύναμης \(W_F\)
\(Γ_4\) Να υπολογίσετε το έργο της τριβής για την μεταφορική κίνηση \(W_T\)
\(Γ_5\) Να υπολογίσετε το έργο της ροπής της τριβής \(W_τ\)
\(Γ_6\) Να υπολογίσετε τη θερμική ενέργεια που παράγεται.
Δίνονται: \(g = 10 \frac{m}{s^2}\) και η ροπή αδράνειας του δίσκου \(I = \frac{m \cdot R^2}{2}\)
\[\underline {Απαντήσεις}\]\(Γ_1\) Η κίνηση του κυλίνδρου είναι σύνθετη κίνηση (κύλιση με ολίσθηση). Η μεταφορική κίνηση είναι ευθύγραμμη ομαλά επιταχυνόμενη και η περιστροφική είναι κυκλική ομαλά επιταχυνόμενη κίνηση. Από τα διαγράμματα:
\[α_{cm} = \frac{Δυ_{cm}}{Δt} \Rightarrow α_{cm} = 1.5 \frac{m}{s^2}\] \[α_{γων} = \frac{Δω}{Δt} \Rightarrow α_{γων} = 5 \frac{rad}{s^2}\]\(Γ_2\) μεταφορική κίνηση
\[ΣF_x = m \cdot α_{cm} \Rightarrow F - T = m \cdot α_{cm} \Rightarrow F - T = 3 \quad (S.I.)\]στροφική κίνηση
\[Στ_k = I_{cm} \cdot α_{γων} \Rightarrow T \cdot R = \frac{m \cdot R^2}{2} \cdot α_{γων} \Rightarrow T = 1Ν\] \[ΣF_y = 0 \Rightarrow N = m \cdot g \Rightarrow N = 20 N\] \[T = μ \cdot N \Rightarrow μ = \frac{T}{N} \Rightarrow μ = 0,05\]\(Γ_3\) Από τη χρονική στιγμή \(t_0 = 0\) ως τη στιγμή \(t_1 = 2 s\).
\[F - T = 3 \Rightarrow F = 4N\] \[Δx_{cm} = \frac{1}{2} \cdot α_{cm} \cdot Δt^2 \Rightarrow Δx_{cm} = 3m\] \[W_F(t_0 \rightarrow t_1) = F \cdot Δx_{cm} \cdot συνθ = 12 Joule\]\(Γ_4\) Για την μεταφορική κίνηση
\[W_T = T \cdot Δx_{cm} συνθ = - Τ \cdot Δx_{cm} = - 3 Joule\]To έργο της τριβής είναι καταναλισκόμενο. Δηλαδή για τη συγκεκριμένη χρονική διάρκεια αφαιρούνται μέσω του έργου της τριβής από τον κύλινδρο \(3 Joule\). Από αυτά ένα μέρος θα επιστρέψει στον κύλινδρο μέσω του έργου της ροπής της τριβής σαν κινητική ενέργεια λόγω περιστροφής και το υπόλοιπο θα χαθεί στο περιβάλλον σαν θερμότητα.
\(Γ_5\) Για την στροφική κίνηση
\[Δθ = \frac{1}{2} \cdot α_{γων} \cdot Δt^2 \Rightarrow Δθ = 10 rad\] \[W_τ = τ_Τ \cdot Δθ \Rightarrow W_τ = Τ \cdot R \cdot Δθ \Rightarrow W_τ = 2 Joule\] \[β) \underline {τρόπος}\] \[ω = α_{γων} \cdot Δt \Rightarrow ω = 10 \frac{rad}{s}\] \[Κ_{στρ} = \frac{1}{2} \cdot I \cdot ω^2 \Rightarrow K_{στρ} = 2 Joule \Rightarrow ΔΚ_{στρ} = W_τ\]\(Γ_6\) Εφαρμόζουμε για τον κύλινδρο την Αρχή Διατήρησης της Ενέργειας.
\[Ε_{αρχ} + Ε_{προσφ} = Ε_{τελ} \Rightarrow 0 + W_F = K_{τελ} + Q\]όπου \(Κ_{τελ} = Κ_{μετ} + Κ_{στρ} = \frac{1}{2} \cdot m \cdot υ^2_{cm} +\frac{1}{2} \cdot I \cdot ω^2\)
\[0+12 = 9+2+Q \Rightarrow Q = 1 Joule\] \[β) \underline {τρόπος}\]Έστω \(Α\) το σημείο επαφής του κυλίνδρου με το οριζόντιο δάπεδο
\[x_Α = Δx_{cm} - Δs \Rightarrow x_Α = Δ_x{cm} - Δθ \cdot R \Rightarrow x_A = 1m\] \[Q = |W_T(t_0 \rightarrow t_1)| = |T \cdot x_{A} \cdot συνθ| = 1 Joule\]ισχύει δηλαδή
\[W_T = W_τ + Q\]blog comments powered by Disqus