Προσομοίωση 2022 Αμερικάνικη Γεωργική Σχολή, Ελληνικό Κολλέγιο, Καλλιτεχνικό Σχολείο Αμπελοκήπων, Πειραματικό Σχολείο Πανεπιστημίου Θεσσαλονίκης, 1ο ΓΕΛ Αξιούπολης, 1ο ΓΕΛ Ευόσμου, 1ο ΓΕΛ Ωραιοκάστρου, 2ο ΓΕΛ Αμπελοκήπων, 2ο ΓΕΛ Εχεδώρου, 2ο ΓΕΛ Καλαμαριάς, 3ο Γυμνάσιο Λαγκαδά και Λυκειακές Τάξεις, 7ο ΓΕΛ Θεσσαλονίκης, 15ο ΓΕΛ Θεσσαλονίκης
ΘΕΜΑ A
Στις ερωτήσεις \(Α_1-Α_4\) να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την
ημιτελή πρόταση.
\(A_1\)
Σε σύστημα ελατηρίου - σώματος, εκτός από τη δύναμη επαναφοράς ενεργεί και δύναμη αντίστασης $F=-b\cdot υ$, όπου $b$ η σταθερά απόσβεσης και $υ$ η ταχύτητα του σώματος. Η σταθερά απόσβεσης εξαρτάται από:
- την ταχύτητα του σώματος που ταλαντώνεται
- την πυκνότητα και το μέγεθος του αντικειμένου που κινείται
- τις ιδιότητες του μέσου, το σχήμα και το μέγεθος του αντικειμένου που κινείται
- τις ιδιότητες του μέσου, την πυκνότητα και τον όγκο του αντικειμένου που κινείται
Μονάδες 5
\(A_2\)
Σύστημα ελατηρίου – μάζας εκτελεί εξαναγκασμένη ταλάντωση. Η συχνότητα του διεγέρτη είναι ίση με την ιδιοσυχνότητα του συστήματος. Αν τετραπλασιάσουμε τη μάζα στο σύστημα, τότε η ιδιοσυχνότητά του:
- γίνεται μέγιστη
- υποδιπλασιάζεται
- διπλασιάζεται
- υποτετραπλασιάζεται
Μονάδες 5
\(A_3\)
Ο \(Oersted\) έδειξε πειραματικά ότι γύρω από έναν ευθύγραμμο ρευματοφόρο αγωγό δημιουργείται μαγνητικό πεδίο, αναζητώντας ένα σύνδεσμο ανάμεσα στον ηλεκτρισμό και στον μαγνητισμό
- στηριζόμενος στην θεωρία του αιθέρα
- βασιζόμενος στον νόμο της επαγωγής του Faraday
- επηρεασμένος από τη φιλοσοφία, η οποία δεχόταν ότι όλα τα φαινόμενα αποτελούν μια ενότητα
- γνωρίζοντας ότι ένα ακίνητο ηλεκτρικό φορτίο δημιουργεί στο χώρο γύρω του ηλεκτρικό πεδίο, ενώ ένα κινούμενο μαγνητικό
Μονάδες 5
\(A_4\)
Η μονάδα έντασης ρεύματος $1 Α$, ορίζεται ως η ένταση του ρεύματος η οποία όταν διαρρέει
- ευθύγραμμο αγωγό μήκους $1 m$, που είναι κάθετος στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου $1 Tesla$, αυτός δέχεται δύναμη $2 \cdot 10^{-7} N$
- ευθύγραμμο αγωγό μήκους $1 m$, που είναι παράλληλος στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου $1 Tesla$, αυτός δέχεται δύναμη $1 Ν$
- κυκλικό ρευματοφόρο αγωγό ακτίνας $1 m$, δημιουργεί στο κέντρο του ένταση μαγνητικού πεδίου $1 Tesla$
- δύο ευθύγραμμους παράλληλους αγωγούς απείρου μήκους, οι οποίοι βρίσκονται στο κενό και σε απόσταση $r = 1m$ ο ένας από τον άλλο, τότε σε τμήμα μήκους $l=1m$ o ένας ασκεί στον άλλο δύναμη $F = 2 \cdot 10^{-7} N$
Μονάδες 5
\(Α_5\)
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
- Σώμα εκτελεί ταυτόχρονα δύο Α.Α.Τ. της ίδιας διεύθυνσης που γίνονται γύρω από το ίδιο σημείο, με το ίδιο πλάτος $Α$ και συχνότητες που διαφέρουν ελάχιστα. Σε αυτήν την περίπτωση η σύνθετη ταλάντωση έχει πλάτος που μεταβάλλεται από $Α$ έως $2A$
- Το μαγνητικό πεδίο στο εσωτερικό ενός κυκλικού ρευματοφόρου αγωγού είναι ομογενές
- Οι σπείρες ενός εύκαμπτου ρευματοφόρου σωληνοειδούς έλκονται πάντα μεταξύ τους
- Η μεταβολή της μαγνητικής ροής είναι το αίτιο και η εμφάνιση της επαγωγικής τάσης το αποτέλεσμα στο φαινόμενο της επαγωγής
- Οι μαγνητικές γραμμές που δημιουργούνται γύρω από ρευματοφόρο αγωγό είναι ανοικτές
Μονάδες 5
ΘΕΜΑ Β
\(Β_1\)
Δίσκος μάζας \(Μ\) είναι στερεωμένος στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς \(k\), και ισορροπεί ακίνητος όπως φαίνεται στο παρακάτω σχήμα. Το άλλο άκρο του ελατηρίου είναι στερεωμένο στο έδαφος. Στο δίσκο τοποθετούμε χωρίς αρχική ταχύτητα σώμα μάζας \(m\). Το σύστημα δίσκος-σώμα εκτελεί απλή αρμονική ταλάντωση.
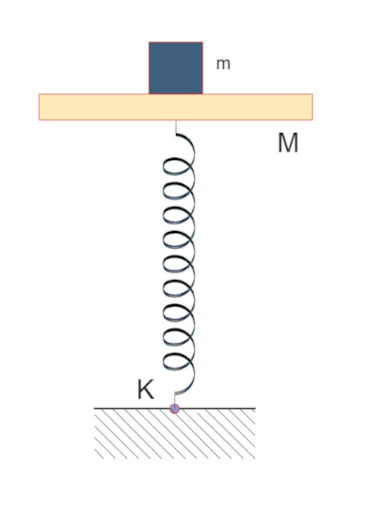
Ι. Η ενέργεια της ταλάντωσης είναι:
\[α. Ε = \frac{m^2 \cdot g^2}{2k} \quad β. Ε = \frac{M^2 \cdot g^2}{2k} \quad γ. Ε=\frac{(M+m)^2g^2}{2k}\]ΙΙ. Το σώμα μάζας \(m\) κατά τη διάρκεια της ταλάντωσης
α. θα εγκαταλείψει το δίσκο
β. δεν θα εγκαταλείψει το δίσκο
Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
Μονάδες 2+6
\(Β_2\)
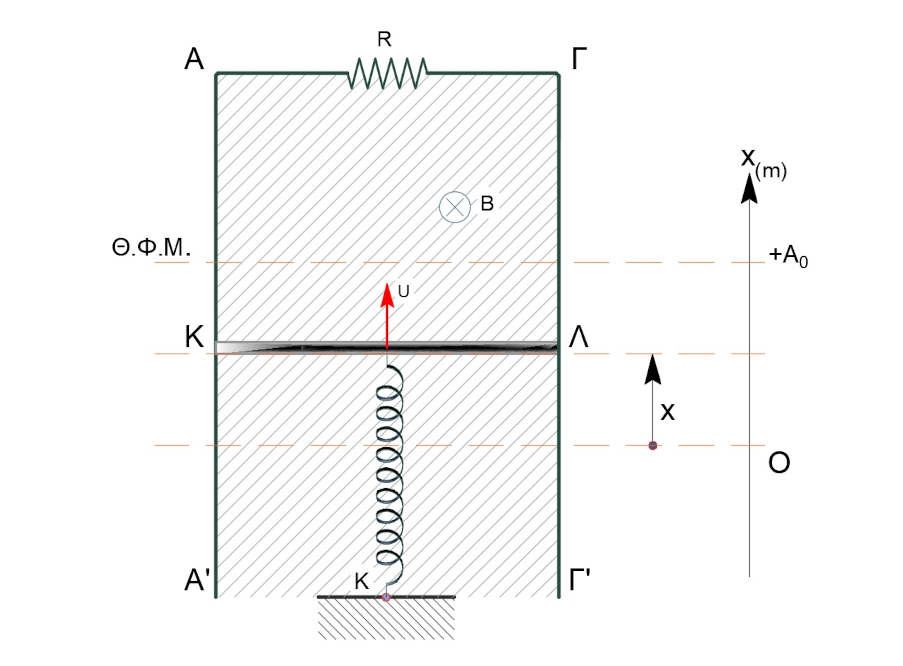
Στην διάταξη του σχήματος, ο αγωγός $ΚΛ$ μήκους $L$, μάζας $m$ και αμελητέας ωμικής αντίστασης, αποτελεί τμήμα ενός κλειστού κυκλώματος που δημιουργούν οι κατακόρυφοι και παράλληλοι αγωγοί-οδηγοί $ΑΑ’, \quad ΓΓ’$ και ο αντιστάτης ωμικής αντίστασης $R$. Οι αγωγοί-οδηγοί $ΑΑ’, \quad ΓΓ’$ έχουν αμελητέα αντίσταση και πάνω τους μπορεί να ολισθαίνει ο αγωγός $ΚΛ$ χωρίς τριβές, παραμένοντας διαρκώς κάθετος σε αυτούς. Τα $A’$ και $Γ’$ καταλήγουν σε οριζόντιο επίπεδο στο οποίο είναι στερεωμένο κατακόρυφο ιδανικό ελατήριο σταθεράς $k$ του οποίου η άλλη άκρη είναι δεμένη στο μέσον του αγωγού $ΚΛ$. Η όλη διάταξη βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο του οποίου η ένταση έχει μέτρο $Β$ με τις δυναμικές γραμμές να έχουν φορά από τον αναγνώστη προς την σελίδα όπως φαίνεται στο σχήμα. Εκτρέπουμε τον αγωγό $ΚΛ$ παράλληλα στον εαυτό του προς τα πάνω έως τη θέση φυσικού μήκους του ελατηρίου και τη χρονική στιγμή $t=0s$ τον αφήνουμε ελεύθερο να κινηθεί. Η κίνηση του αγωγού είναι φθίνουσα ταλάντωση με πολύ μικρή σταθερά απόσβεσης $b$ και περίοδο ίση με την περίοδο της \(Α.Α.Τ.\) που θα έκανε ο αγωγός αν δεν υπήρχε το μαγνητικό πεδίο. Αν γνωρίζετε την σχέση \(Λ = \frac{b}{2m}\) που συνδέει τον εκθέτη απόσβεσης $Λ$ με τη σταθερά απόσβεσης $b$ και τη μάζα $m$ του αγωγού, ο λόγος του αρχικού πλάτους ταλάντωσης προς το πλάτος της φθίνουσας ταλάντωσης σε χρόνο μιας περιόδου είναι:
\[α. e^{\frac{π \cdot B^2 \cdot L^2}{R} \sqrt{\frac{1}{m\cdot k}} } \quad β. e^{-\frac{B^2 \cdot L^2}{R} \sqrt{\frac{1}{m\cdot k}} } \quad γ. e^{\frac{B^2 \cdot L^2}{2R \sqrt{m\cdot k} } }\]Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
Μονάδες 2+6
\(Β_3\)
Ομάδα μαθητών εκτελούν την εργαστηριακή άσκηση “Μέτρηση δύναμης Laplace με ζυγό ρεύματος”. Για τον λόγο αυτό χρησιμοποιούν σωληνοειδές διαμέτρου \(10.0 \quad cm\) και μήκους \(75.0 \quad cm\) που είναι κατασκευασμένο από χάλκινο σύρμα διαμέτρου \(0.1 \quad cm\) με πολύ λεπτή μόνωση. Το σύρμα είναι τυλιγμένο σε μια στρώση γύρω από έναν χάρτινο σωλήνα, με τις σπείρες να εφάπτονται η μία με την άλλη. Το πείραμά τους γίνεται σε θερμοκρασία δωματίου \(θ \simeq 20^o C\)
Η ηλεκτρική ισχύς που πρέπει να αποδίδεται στο σωληνοειδές ώστε στο κέντρο του να παράγεται μαγνητικό πεδίο μέτρου \(8.0 \quad mT\) είναι:
\[α. 204 Watt \quad β. 2.04 Watt \quad γ. 300 Watt\]Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας. Δίνεται \(π^2 \simeq 10 \quad k_μ = 10^{-7} \frac{N}{A^2}\)
Μονάδες 2+9
θέμα Γ
Στο παρακάτω σχήμα οι αγωγοί \(ΑΓ\), \(ΔΖ\), απείρου μήκους, βρίσκονται στο ίδιο κατακόρυφο επίπεδο, είναι παράλληλοι μεταξύ τους, απέχουν \(ℓ=1m\) και έχουν μηδενική ωμική αντίσταση. Η ράβδος \(ΚΛ\) έχει μήκος \(ℓ=1m\) μάζα \(m = 2 kg\), αντίσταση \(R_{ΚΛ}=2Ω\) και αρχικά είναι ακίνητη. Η ράβδος \(ΚΛ\) μπορεί να κινείται χωρίς τριβές, παραμένοντας συνεχώς κάθετη και σε επαφή με τους αγωγούς \(ΑΓ\), \(ΔΖ\). Η γεννήτρια εναλλασσόμενου ρεύματος που συνδέεται στα άκρα \(Α\), \(Δ\) περιέχει αγώγιμο πλαίσιο εσωτερικής αντίστασης \(R_π = 6Ω\), το οποίο στρέφεται με σταθερή γωνιακή ταχύτητα \(ω\) γύρω από άξονα που βρίσκεται στο επίπεδό του και είναι κάθετος στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου. Η χρονική εξίσωση της στιγμιαίας τιμής της εναλλασσόμενης τάσης που εμφανίζεται στο πλαίσιο είναι \(υ = V_o \cdot ημ(50πt) \quad S.I.\)
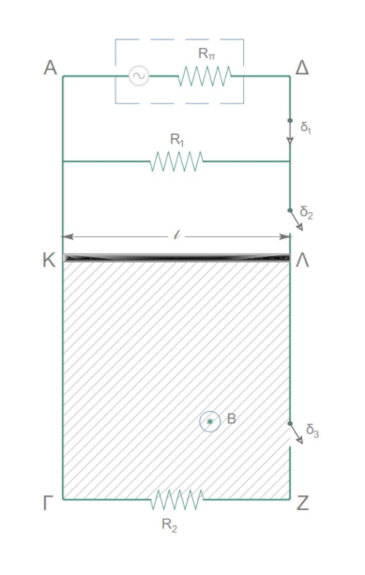
Για τον αντιστάτη \(R_1\) δίνονται τα κανονικά στοιχεία λειτουργίας του (\(6 Watt/6 Volt\)), ενώ για τον αντιστάτη \(R_2\) δίνεται η ωμική του αντίσταση \(R_2 = 3Ω\). Από την αρχική θέση της ράβδου \(ΚΛ\) και στον χώρο κάτω απ’ αυτήν, υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης \(B\), του οποίου οι δυναμικές γραμμές έχουν διεύθυνση κάθετη στο επίπεδο της σελίδας και φορά προς τον αναγνώστη, όπως φαίνεται στο σχήμα και καλύπτει όλη τη γραμμοσκιασμένη περιοχή.
Γ1. Αρχικά ο διακόπτης \(δ_1\) είναι κλειστός και οι \(δ_2\), \(δ_3\) είναι ανοικτοί. Τότε, η μέση ισχύς στον αντιστάτη \(R_1\) ισούται με \(24 Watt\). Υπολογίστε το πλάτος της τάσης \(V_o\) και την ενεργό ένταση του ρεύματος στον αντιστάτη \(R_1\).
Μονάδες 6
Γ2. Διατηρώντας τον διακόπτη \(δ_1\) κλειστό και ανοιχτούς τους διακόπτες \(δ_2\) και \(δ_3\), μεταβάλλουμε τη συχνότητα περιστροφής του πλαισίου στη γεννήτρια εναλλασσόμενης τάσης, ώστε ο αντιστάτης \(R_1\) να λειτουργεί κανονικά. Η στιγμιαία τιμή της τάσης που παράγεται τότε έχει τη μορφή \(υ’ = V_ο’ \cdot ημ(ω’t)\). Να βρεθεί η νέα συχνότητα περιστροφής του πλαισίου.
Μονάδες 5
Γ3. Τη χρονική στιγμή \(t_ο = 0\), ανοίγουμε τον διακόπτη \(δ_1\) και αφήνουμε την ράβδο \(ΚΛ\) ελεύθερη να κινηθεί. Τη στιγμή \(2 sec\) κλείνουμε τους διακόπτες \(δ_2\) και \(δ_3\) και παρατηρούμε ότι έκτοτε η ράβδος κινείται με σταθερή ταχύτητα. Υπολογίστε το μέτρο της έντασης \(B\) του μαγνητικού πεδίου μέσα στο οποίο κινείται η ράβδος.
Μονάδες 7
Γ4. Για το χρονικό διάστημα 0 έως \(5 sec\), να υπολογίσετε το ποσοστό επί τοις εκατό της δυναμικής ενέργειας που μετατρέπεται σε θερμότητα στον αντιστάτη \(R_2\).
Δίνεται \(g = 10 \frac{m}{s^2}\)
Μονάδες 7
θέμα Δ
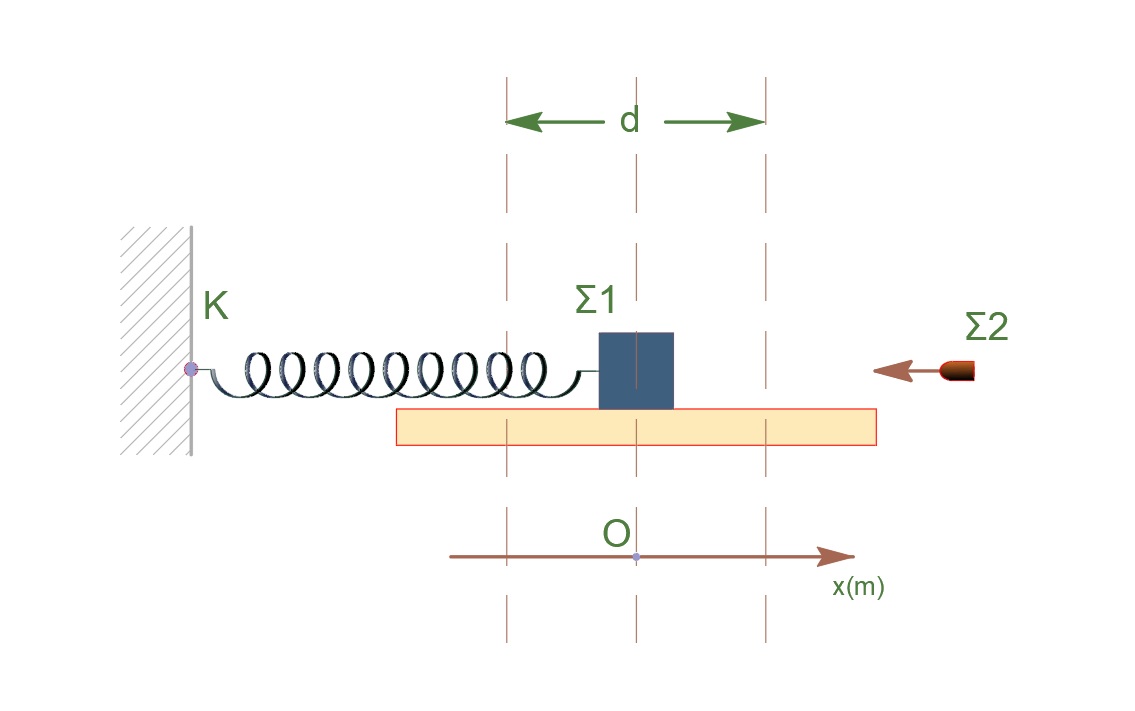
Σώμα \(Σ_1\) μάζας \(m = 50 \quad g\) ισορροπεί ακίνητο πάνω σε οριζόντια βάση, δεμένο στην άκρη ενός οριζόντιου ελατηρίου, η άλλη άκρη του οποίου είναι στερεωμένη σε ακίνητο σημείo \(K\) κατακόρυφου τοίχου όπως φαίνεται στο σχήμα. Δεύτερο σώμα \(Σ_2\) ίσης μάζας που κινείται στη διεύθυνση του άξονα του ελατηρίου συγκρούεται με τον σώμα \(Σ_1\) και σφηνώνεται ακαριαία σε αυτό. Το συσσωμάτωμα \(Σ\) που προκύπτει μπορεί να κινείται χωρίς τριβές και εκτελεί απλή αρμονική ταλάντωση μεταξύ δύο ακραίων θέσεων που απέχουν απόσταση \(d = 2 \quad cm\). Ο ελάχιστος χρόνος μετάβασης του συσσωματώματος από τη μια ακραία θέση στην άλλη είναι \(Δt_1 = 0.1π \quad s\).
Δ1. Να γράψετε τη χρονική εξίσωση της απομάκρυνσης \(x_1 = f(t)\) του συσσωματώματος \(Σ\), γύρω από τη θέση ισορροπίας του \(Ο\) Θεωρώντας ότι τη χρονική στιγμή μηδέν το συσσωμάτωμα βρίσκεται στο σημείο \(Ο\) και κινείται κατά την αρνητική φορά.
Μονάδες 5
Δ2 Να υπολογίσετε την ενέργεια που μετατρέπεται σε θερμότητα κατα την πλαστική κρούση.
Στη συνέχεια αφαιρείται το ελατήριο από το συσσωμάτωμα και αντικαθίσταται η οριζόντια λεία επιφάνεια της βάσης με νέα βάση για την οποία ο συντελεστής στατικής τριβής μεταξύ του συσσωματώματος \(Σ\) και της βάσης είναι \(μ_σ = \sqrt3\). Με κατάλληλο μηχανισμό η νέα βάση εκτελεί απλή αρμονική ταλάντωση σε διεύθυνση ίδια με την προηγούμενη και γύρω από την ίδια θέση ισορροπίας \(Ο\) με πλάτος και συχνότητα ταλάντωσης \(Α_2 = \sqrt3 \quad cm\) και \(f_2 = \frac{5}{π} \quad Hz\) αντίστοιχα.
Μονάδες 5
Δ3. Αν γνωρίζετε ότι τη χρονική στιγμή \(t_o = 0\) η νέα βάση βρίσκεται στην ακραία θέση της και ο ρυθμός μεταβολής της ταχύτητάς της είναι αρνητικός, να δείξετε ότι το συσσωμάτωμα \(Σ\) δεν ολισθαίνει για όσο χρόνο κινείται η βάση και να γράψετε τη χρονική εξίσωση της απομάκρυνσης \(x_2 = f(t)\) του συσσωματώματος \(Σ\) γύρω από τη θέση ισορροπίας \(Ο\).
Μονάδες 5
Δ4. Να γράψετε τη χρονική εξίσωση της ταχύτητας \(υ = f(t)\) της σύνθετης ταλάντωσης που εκτελεί το συσσωμάτωμα \(Σ\) γύρω από τη ίδια θέση ισορροπίας του \(Ο\) στην ίδια διεύθυνση, αν θεωρήσουμε ότι μπορεί να κάνει ταυτόχρονα τις δύο προηγούμενες αρμονικές ταλαντώσεις \(x_1 = f(t)\) και \(x_2 = f(t)\).
Μονάδες 5
Δ5 Όταν η απομάκρυνση του συσσωματώματος \(Σ\) από τη θέση ισορροπίας \(Ο\) λόγω της πρώτης ταλάντωσης είναι \(x_1 = 0.5 \quad cm\) και η ταχύτητά του είναι θετική, να βρείτε το ρυθμό μεταβολής της ορμής του συσσωματώματος για τη σύνθετη ταλάντωση.
Μονάδες 5
blog comments powered by Disqus