Πηγή εναλλασσόμενης τάσης

θέμα Γ

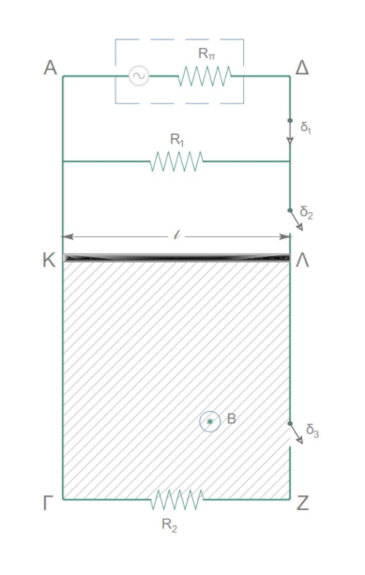
Στο παρακάτω σχήμα οι αγωγοί \(ΑΓ\), \(ΔΖ\), απείρου μήκους, βρίσκονται στο ίδιο κατακόρυφο επίπεδο, είναι παράλληλοι μεταξύ τους, απέχουν \(ℓ=1m\) και έχουν μηδενική ωμική αντίσταση. Η ράβδος \(ΚΛ\) έχει μήκος \(ℓ=1m\) μάζα \(m = 2 kg\), αντίσταση \(R_{ΚΛ}=2Ω\) και αρχικά είναι ακίνητη. Η ράβδος \(ΚΛ\) μπορεί να κινείται χωρίς τριβές, παραμένοντας συνεχώς κάθετη και σε επαφή με τους αγωγούς \(ΑΓ\), \(ΔΖ\). Η γεννήτρια εναλλασσόμενου ρεύματος που συνδέεται στα άκρα \(Α\), \(Δ\) περιέχει αγώγιμο πλαίσιο εσωτερικής αντίστασης \(R_π = 6Ω\), το οποίο στρέφεται με σταθερή γωνιακή ταχύτητα \(ω\) γύρω από άξονα που βρίσκεται στο επίπεδό του και είναι κάθετος στις δυναμικές γραμμές ομογενούς μαγνητικού πεδίου. Η χρονική εξίσωση της στιγμιαίας τιμής της εναλλασσόμενης τάσης που εμφανίζεται στο πλαίσιο είναι \(υ = V_o \cdot ημ(50πt) \quad S.I.\) Για τον αντιστάτη \(R_1\) δίνονται τα κανονικά στοιχεία λειτουργίας του (\(6 Watt/6 Volt\)), ενώ για τον αντιστάτη \(R_2\) δίνεται η ωμική του αντίσταση \(R_2 = 3Ω\). Από την αρχική θέση της ράβδου \(ΚΛ\) και στον χώρο κάτω απ’ αυτήν, υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης \(B\), του οποίου οι δυναμικές γραμμές έχουν διεύθυνση κάθετη στο επίπεδο της σελίδας και φορά προς τον αναγνώστη, όπως φαίνεται στο σχήμα και καλύπτει όλη τη γραμμοσκιασμένη περιοχή.

Γ1. Αρχικά ο διακόπτης \(δ_1\) είναι κλειστός και οι \(δ_2\), \(δ_3\) είναι ανοικτοί. Τότε, η μέση ισχύς στον αντιστάτη \(R_1\) ισούται με \(24 Watt\). Υπολογίστε το πλάτος της τάσης \(V_o\) και την ενεργό ένταση του ρεύματος στον αντιστάτη \(R_1\).

Γ2. Διατηρώντας τον διακόπτη \(δ_1\) κλειστό και ανοιχτούς τους διακόπτες \(δ_2\) και \(δ_3\), μεταβάλλουμε τη συχνότητα περιστροφής του πλαισίου στη γεννήτρια εναλλασσόμενης τάσης, ώστε ο αντιστάτης \(R_1\) να λειτουργεί κανονικά. Η στιγμιαία τιμή της τάσης που παράγεται τότε έχει τη μορφή \(υ’ = V_ο’ \cdot ημ(ω’t)\). Να βρεθεί η νέα συχνότητα περιστροφής του πλαισίου.

Γ3. Τη χρονική στιγμή \(t_ο = 0\), ανοίγουμε τον διακόπτη \(δ_1\) και αφήνουμε την ράβδο \(ΚΛ\) ελεύθερη να κινηθεί. Τη στιγμή \(2 sec\) κλείνουμε τους διακόπτες \(δ_2\) και \(δ_3\) και παρατηρούμε ότι έκτοτε η ράβδος κινείται με σταθερή ταχύτητα. Υπολογίστε το μέτρο της έντασης \(B\) του μαγνητικού πεδίου μέσα στο οποίο κινείται η ράβδος.

Γ4. Για το χρονικό διάστημα 0 έως \(5 sec\), να υπολογίσετε το ποσοστό επί τοις εκατό της δυναμικής ενέργειας που μετατρέπεται σε θερμότητα στον αντιστάτη \(R_2\).

Δίνεται \(g = 10 \frac{m}{s^2}\)