Μοριοδότηση 2021
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(δ\)
Α3 - \(γ\)
Α4 - \(β\)
Α5: \(Σ - Λ - Σ - Σ - Λ\)
Θέμα Β
B1-\((ii)-2-6\)
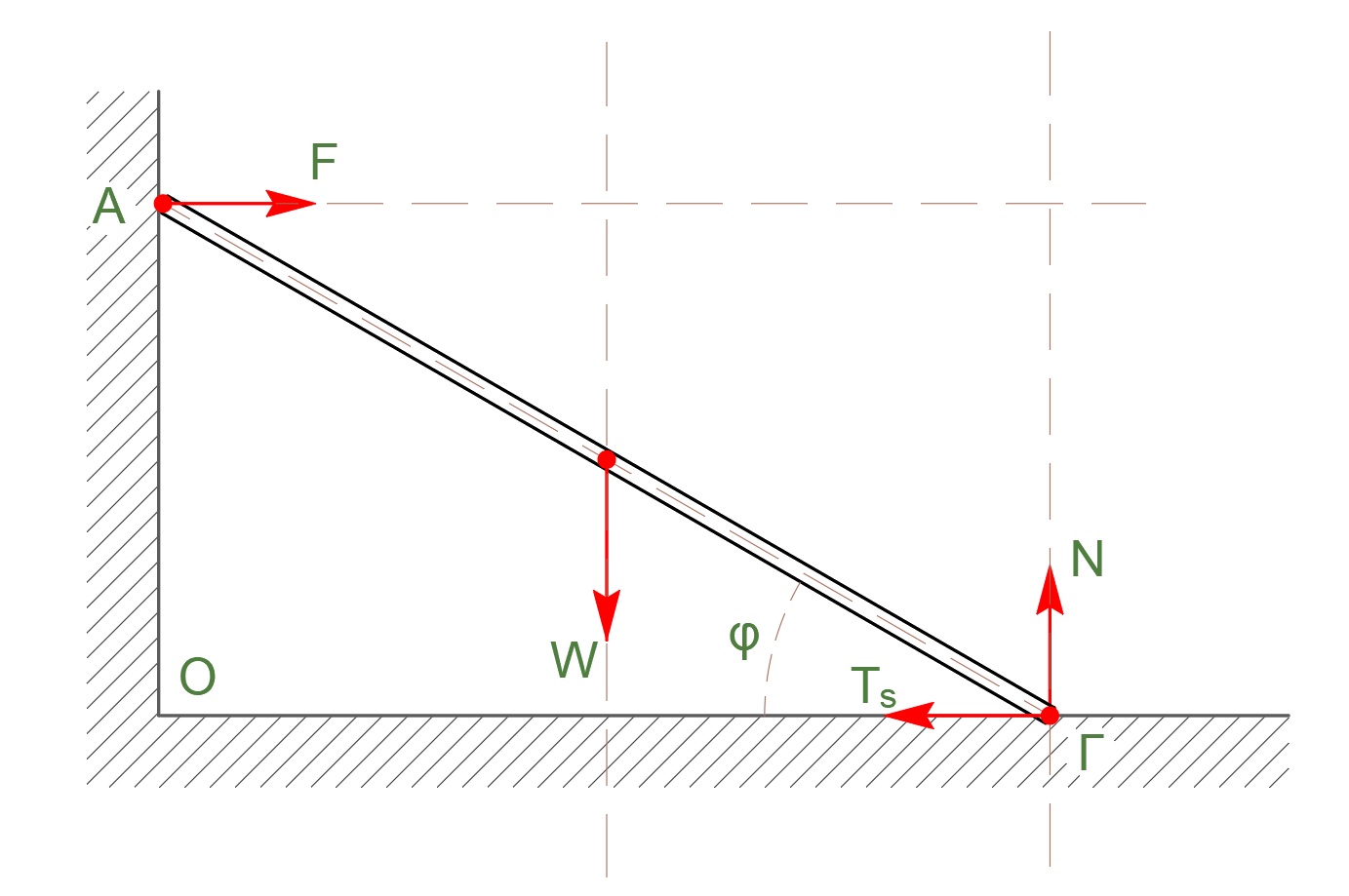
σκάλα ισορροπία \(Σ\vecτ_Γ = \vec0\)
\[\vecτ_W + \vecτ_F = \vec0 \Rightarrow W \cdot \frac{l}{2} \cdot συνφ = F \cdot l \cdot ημφ\] \[\vecτ_W + \vecτ_F = \vec0 \Rightarrow W_y \cdot \frac{l}{2} = F_y \cdot l \Rightarrow W \cdot συνφ \cdot \frac{l}{2} = F \cdot ημφ \cdot l\]σκάλα ισορροπία \(Σ \vec{F_x} = \vec0 \Rightarrow F = T_s\)
σκάλα ισορροπία \(Σ \vec{F_y} = \vec0 \Rightarrow W = N\)
\[N \cdot \frac{l}{2} \cdot συνφ = T_s \cdot l \cdot ημφ \Rightarrow T_s = \frac{N}{2 \cdot εφφ}\]στατική τριβή \(0 \le T_s \le μ \cdot N\)
\[T_s \le μ \cdot N \Rightarrow \frac{1}{2 \cdot εφφ} \le μ \Rightarrow εφφ \ge \frac{1}{2μ}\]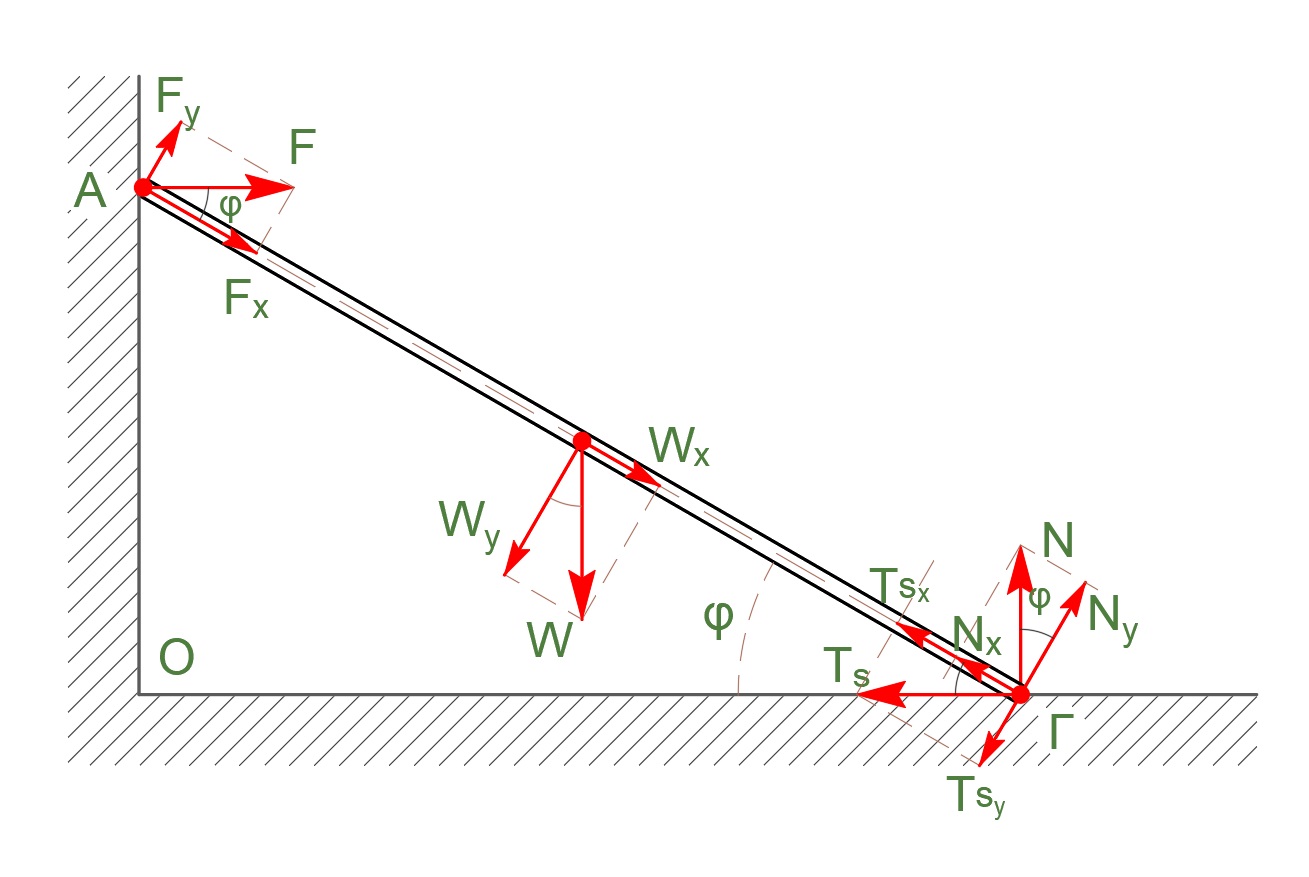
σκάλα ισορροπία \(Σ\vecτ_Α = \vec0\)
\[\vecτ_W + \vecτ_Ν + \vecτ_{Τ_s} = \vec0 \Rightarrow W \cdot \frac{l}{2} \cdot συνφ + T_s \cdot l \cdot ημφ = Ν \cdot l \cdot συνφ\] \[\vecτ_W + \vecτ_Ν + \vecτ_{Τ_s} = \vec0 \Rightarrow W_y \cdot \frac{l}{2} + T_{s_y} \cdot l = Ν_y \cdot l \cdot\]σκάλα ισορροπία \(Σ \vec{F_y} = \vec0 \Rightarrow W = N\)
\[W \cdot \frac{l}{2} \cdot συνφ + T_s \cdot l \cdot ημφ = W \cdot l \cdot συνφ \Rightarrow T_s = \frac{W}{2 \cdot εφφ}\]στατική τριβή \(0 \le T_s \le μ \cdot N\)
\[T_s \le μ \cdot N \Rightarrow \frac{1}{2 \cdot εφφ} \le μ \Rightarrow εφφ \ge \frac{1}{2μ}\]άρα σωστό το \(ii\)
Β2 - \((i)-2-6\)
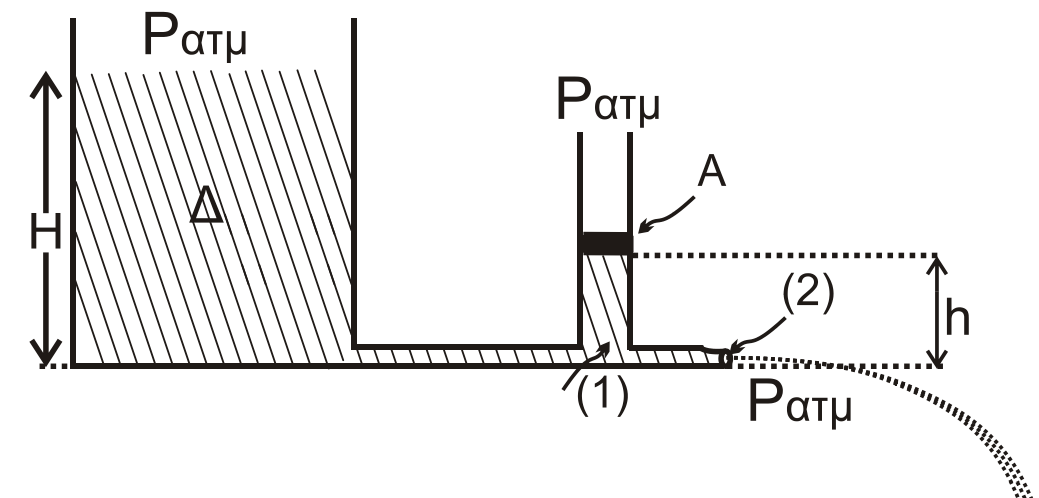
Bernoulli \((0 \rightarrow 2)\)
\[P_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_0^2 + ρ \cdot g \cdot H = P_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_2^2 + 0\]Bernoulli \((1 \rightarrow 2)\)
\[P_1 + \frac{1}{2} \cdot ρ \cdot υ_1^2 = P_{ατμ} + \frac{1}{2} \cdot ρ \cdot υ_2^2\]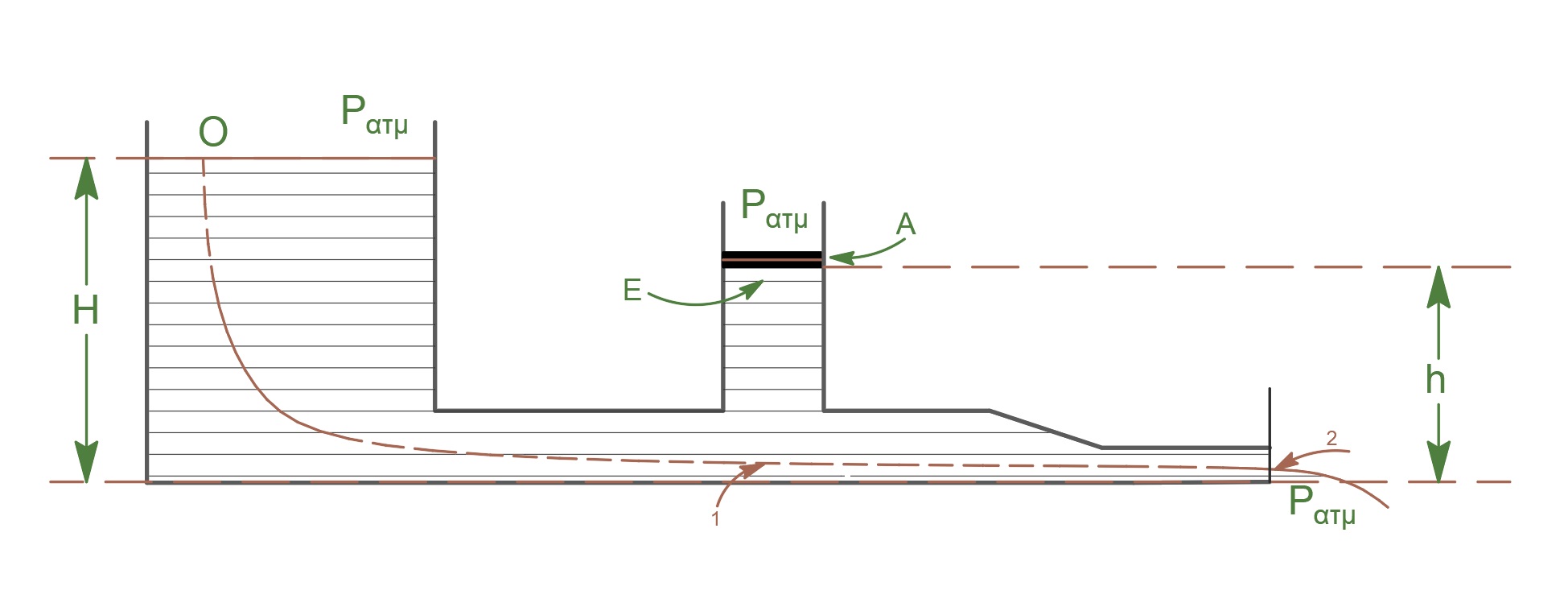
Εξίσωση συνέχειας \((1 \rightarrow 2)\)
\[Π_1 = Π_2 \Rightarrow A_1 \cdot υ_1 = Α_2 \cdot υ_2 \Rightarrow υ_1 = \frac{υ_2}{2}\] \[α) \underline {τρόπος}\]έμβολο ισορροπία \(Σ \vec{F} = \vec0\)
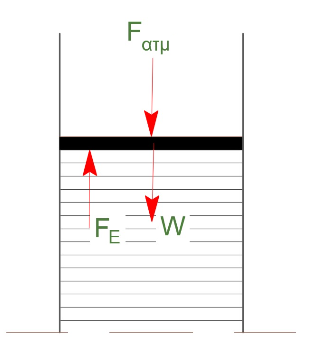
Θεμελιώδης νόμος της υδροστατικής
\[P_1 = P_E + ρ \cdot g \cdot \frac{H}{4}\] \[β) \underline {τρόπος}\]Η ολική πίεση \(P_1\) είναι υδροστατική και ατμοσφαιρική και η πίεση του εμβόλου άρα:
\[P_1 = P_{ατμ} + \frac{w}{A} + ρ \cdot g \cdot \frac{H}{4}\]μετά τις πράξεις
\[W = \frac{ρ \cdot g \cdot H \cdot A}{2}\]άρα σωστό το \(i\)
Β3 - \((iii)-2-7\)
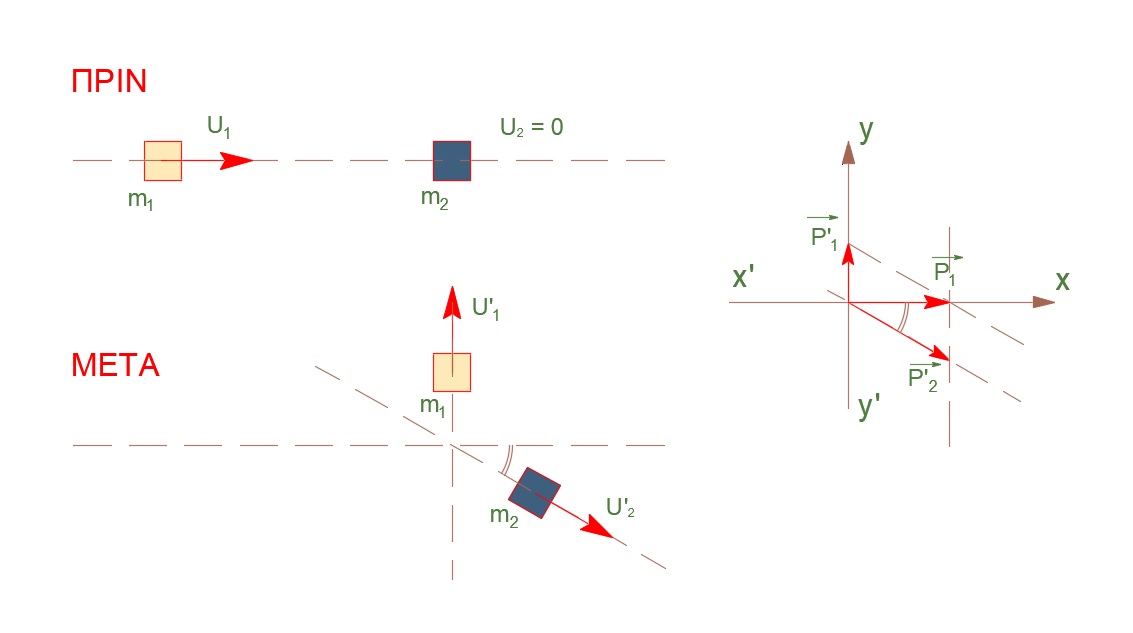
Ελαστική κρούση
\[Σ\vec{F}_x^{εξ} = \vec0 \Rightarrow A.Δ.Ο.(x)\] \[\vec{p}_{πριν} = \vec{p}_{μετά} \Rightarrow m_1 \cdot υ_1 = m_2 \cdot υ_2' \cdot συνφ\] \[Σ\vec{F}_y^{εξ} = \vec0 \Rightarrow A.Δ.Ο.(y)\] \[\vec{p}_{πριν} = \vec{p}_{μετά} \Rightarrow 0 = m_1 \cdot υ_1' - m_2 \cdot υ_2' \cdot ημφ\] \[υ_1' = \frac{υ_1}{\sqrt3}\] \[β) \underline {τρόπος}\]Ελαστική κρούση
\[ημφ = \frac{p_1'}{p_2'} \Rightarrow \frac{1}{2} = \frac{p_1'}{p_2'} \Rightarrow p_2' = 2\cdot p_1'\] \[p_2'^2 = p_1'^2 + p_1^2 \Rightarrow 4 \cdot p_1'^2 = p_1'^2 + p_1^2\] \[p_1' = \frac{p_1}{\sqrt3} \Rightarrow υ_1' = \frac{υ_1}{\sqrt3}\] \[γ) \underline {τρόπος}\]Ελαστική κρούση
\[εφφ = \frac{p_1'}{p_1} \Rightarrow υ_1' = \frac{υ_1}{\sqrt3}\] \[δ) \underline {τρόπος}\]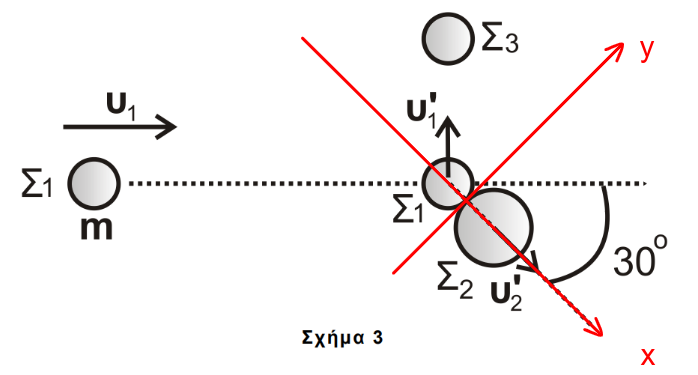
άξονας x’x διάκεντρος, άξονας y’y κάθετος στην διάκεντρο.
Άξονας x’x κεντρική και ελαστική κρούση με ακίνητο σώμα \(Σ_2\)
\[υ'_{1x} = \frac{m_1 - m_2}{m_1 + m_2} \cdot υ_{1x} \Rightarrow υ'_{1x} = \frac{m - 2m}{m + 2m} \cdot υ_1 \cdot συν30^ο\] \[υ'_{1x} = -\frac{υ_1 \sqrt3}{6}\]άξονας y’y η ορμή του \(Σ_1\) παραμένει σταθερή
\[υ'_{1y} = υ_{1y} \Rightarrow υ'_{1y} = υ_1 \cdot ημφ \Rightarrow υ'_{1y} = \frac{υ_1}{2}\] \[υ'_1 = \sqrt{(υ'_{1x})^2 + (υ'_{1y})^2 } \Rightarrow υ'_1 = \frac{υ_1}{\sqrt3}\] \[ε) \underline {τρόπος}\]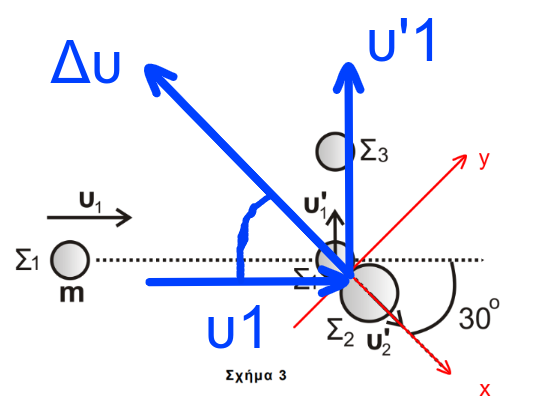
Το \(Σ_1\) δέχετε ώθηση \(Ω\) που έχει την διεύθυνση της διακέντρου x’x και φορά αντίθετη της \(υ'_2\)
\[Σ_1: \quad \vec{p_{αρχ}} + \vec{Ω} = \vec{p_{τελ}} \Rightarrow m_1 \cdot \vec{υ_1} + m_1 \cdot Δ\vec{υ} = m_1 \cdot \vec{υ'_1}\] \[\vec{υ_1} + Δ\vec{υ} = \vec{υ'_1} \Rightarrow Δ\vec{υ} = \vec{υ'_1} - \vec{υ_1}\] \[συν30^ο = \frac{υ_1}{Δυ} \Rightarrow Δυ = \frac{2 υ_1}{ \sqrt3}\] \[ημ30^ο = \frac{υ'_1}{Δυ} \Rightarrow Δυ = 2\cdot υ'_1\]και μετά τις πράξεις
\[υ'_1 = \frac{υ_1}{\sqrt3}\]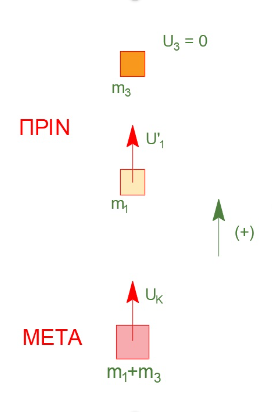
Πλαστική κρούση
\[Σ\vec{F}_{εξ} = \vec0 \Rightarrow A.Δ.Ο.\] \[\vec{p}_{πριν} = \vec{p}_{μετά} \Rightarrow m_1 \cdot υ_1' = (m_1 + m_2) \cdot V_k\] \[\frac{K_{συσ}}{Κ_1} = \frac{\frac{1}{2} (m_1+m_3) \cdot V_k^2}{\frac{1}{2} m_1 \cdot υ_1^2}\]και μετά τις πράξεις
\[\frac{K_{συσ}}{Κ_1} = \frac{1}{6}\]άρα σωστό το \(iii\)
Θέμα Γ
Γ1-\((6)\)
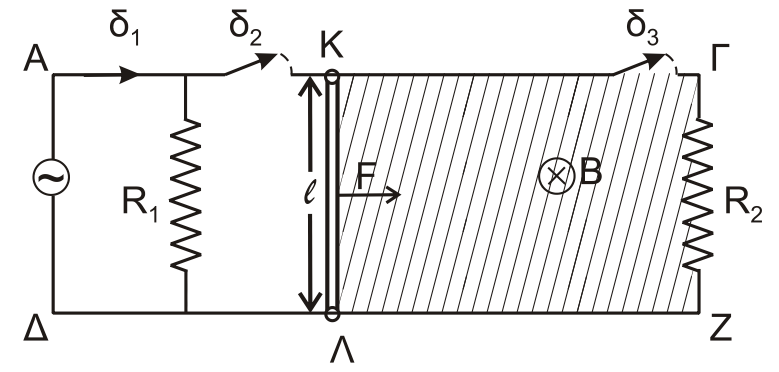
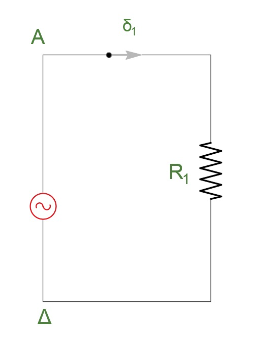
Γ2-\((6)\)
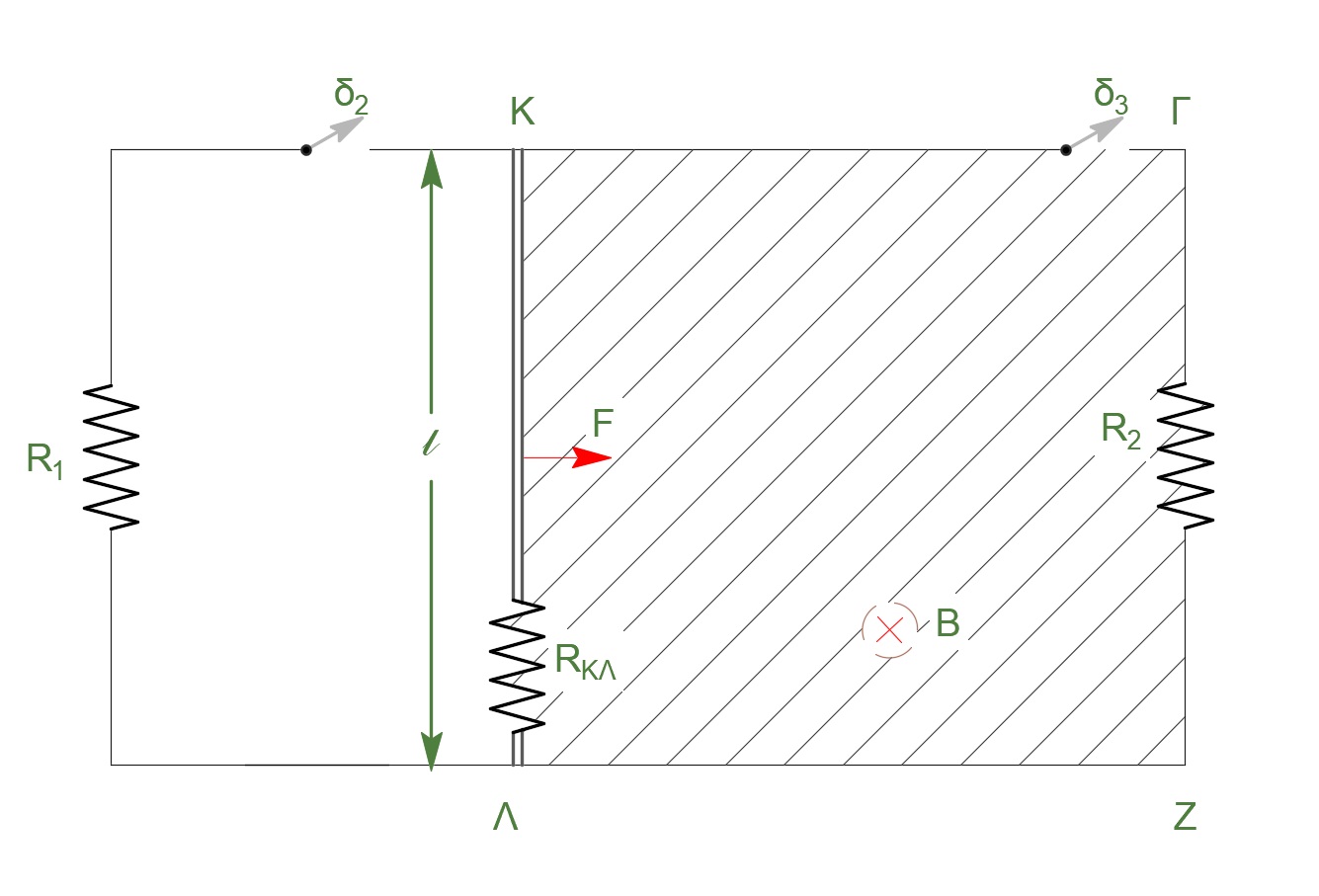
Γ3-\((6)\)
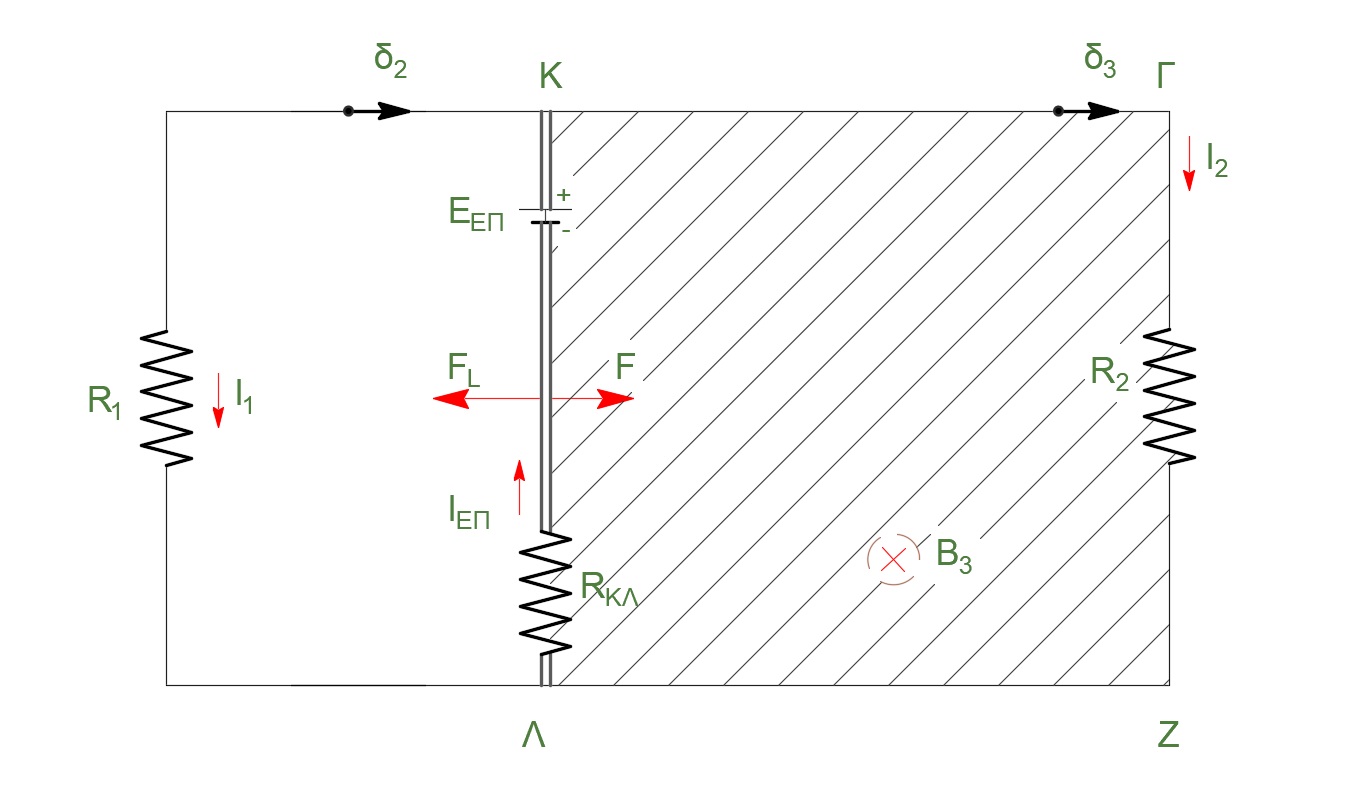
ράβδος ΚΛ \(Σ\vec{F} = m \cdot α \Rightarrow α = \frac{F}{m} \Rightarrow α = 1 \frac{m}{s^2}\)
Ομαλά επιταχυνόμενη κίνηση
\[υ_ο = α \cdot t \Rightarrow υ_ο = 2 \frac{m}{s}\]t=2s
\[E_{επ} = |- \frac{ΔΦ}{Δt} | = | - \frac{B \cdot ΔS}{Δt} | = B \cdot υ_ο \cdot l\] \[υ_ο = σταθ. \quad \Rightarrow α = 0 \quad \Rightarrow ΣF = 0\] \[F = F_L \quad F_L = B \cdot I_{επ} \cdot l \quad I_{επ} = \frac{E_{επ}}{R_{ολ}}\] \[\frac{1}{R_π} = \frac{1}{R_1} + \frac{1}{R_2} \Rightarrow R_π = 2 Ω\] \[R_{ολ} = R_π + R_{ΚΛ} \Rightarrow R_{ολ} = 4 Ω\]και μετά τις πράξεις έχουμε \(Β = 1Τ\)
Γ4-\((7)\)
\[α) \underline {τρόπος}\] \[E_{επ} = Β \cdot υ_ο \cdot l \Rightarrow E_{επ} = 2 Volt\] \[E_{επ} = I_{επ} \cdot R_{ολ} \Rightarrow I_{επ} = 0.5 A\] \[V_{ΚΛ} = Ι_{επ} \cdot R_π \Rightarrow V_{ΚΛ} = 1 Volt\] \[V_{ΚΛ} = E_{επ} - Ι_{επ} \cdot R_{ΚΛ} \Rightarrow V_{ΚΛ} = 1 Volt\] \[Ι_2 = \frac{V_{ΚΛ}}{R_2} \Rightarrow I_2 = \frac{1}{3} A\] \[Q_2 = I_2^2 \cdot R_2 \cdot Δt \Rightarrow Q_2 = 1 Joule\]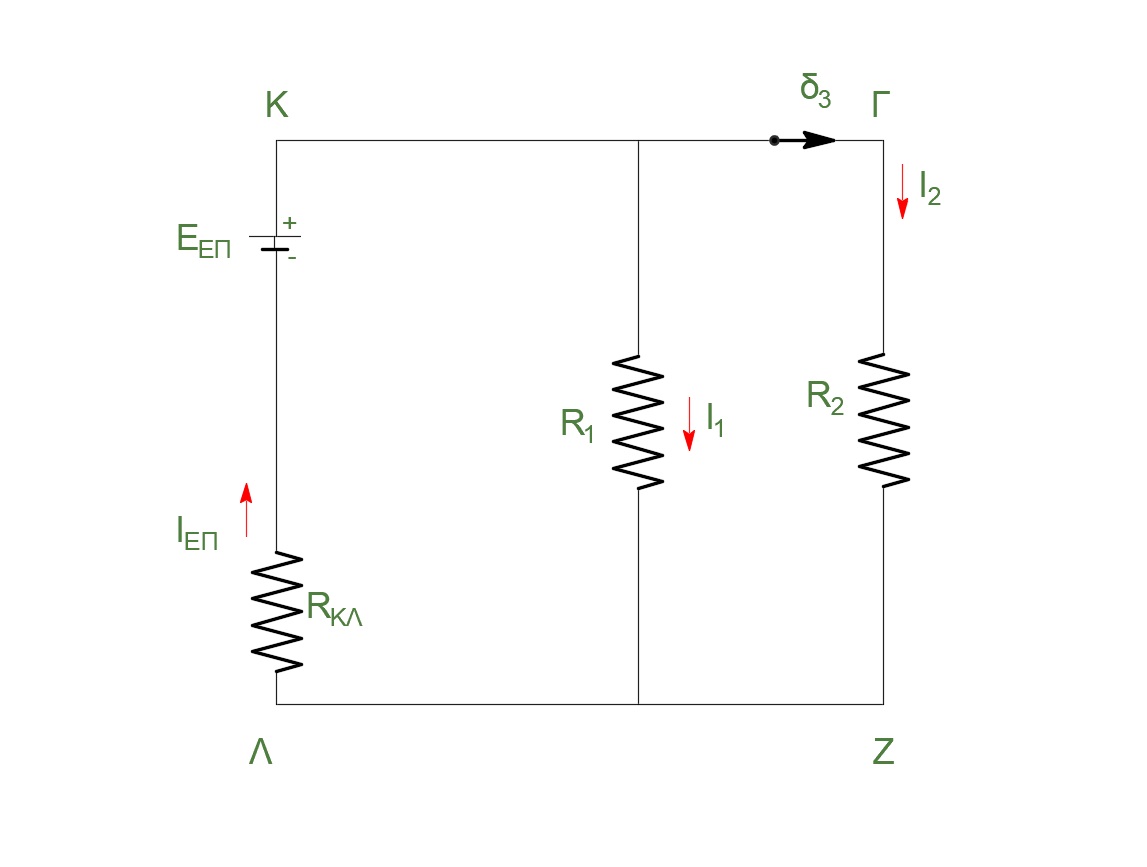
Θ.Μ.Κ.Ε \((t_1 = 2s \rightarrow t_2 = 5s)\)
\[ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_F + W_{F_L}\] \[Δx = υ_ο \cdot Δt \Rightarrow Δx = 6m\] \[0 = F \cdot Δx + W_{F_L} \Rightarrow W_{F_L} = -3 Joule\] \[Q_{ολ} = |W_{F_L}| \Rightarrow Q_{ολ} = 3 Joule\] \[Q_{ολ} = Q_1 + Q_2 + Q_{ΚΛ}\] \[Q = I^2 \cdot R \cdot Δt \Rightarrow Q = \frac{V^2}{R} \cdot Δt\] \[\frac{Q_1}{Q_2} = \frac{R_2}{R_1} \Rightarrow \frac{Q_1}{Q_2} = \frac{1}{2}\] \[Q_{ΚΛ} = Ι_{επ}^2 \cdot R_{ΚΛ} \cdot Δt \quad Q_{1,2} = I_{επ}^2 \cdot R_π \cdot Δt\] \[\frac{Q_{ΚΛ}}{Q_{1,2}} = \frac{R_{ΚΛ}}{R_π} \Rightarrow \frac{Q_{ΚΛ}}{Q_{1,2}} = 1\]και μετά τις πράξεις \(Q_2 = 1 Joule\)
\[t_o = 0 \rightarrow t_1 = 2s\] \[Δx_1 = \frac{1}{2} \cdot α \cdot t_1^2 \Rightarrow Δx_1 = 2m\] \[t_1 = 2s \rightarrow t_2 = 5s\] \[Δx_2 = υ_ο \cdot Δt \Rightarrow Δx_2 = 6m\] \[W_F = F \cdot (Δx_1 + Δx_2) \Rightarrow W_F = 4 Joule\] \[Π(\%) = \frac{Q_2}{W_F} \cdot 100 \% \Rightarrow Π(\%) = 25\%\]Θέμα Δ
Δ1-\((7)\)
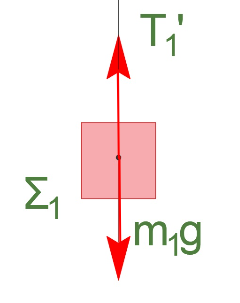
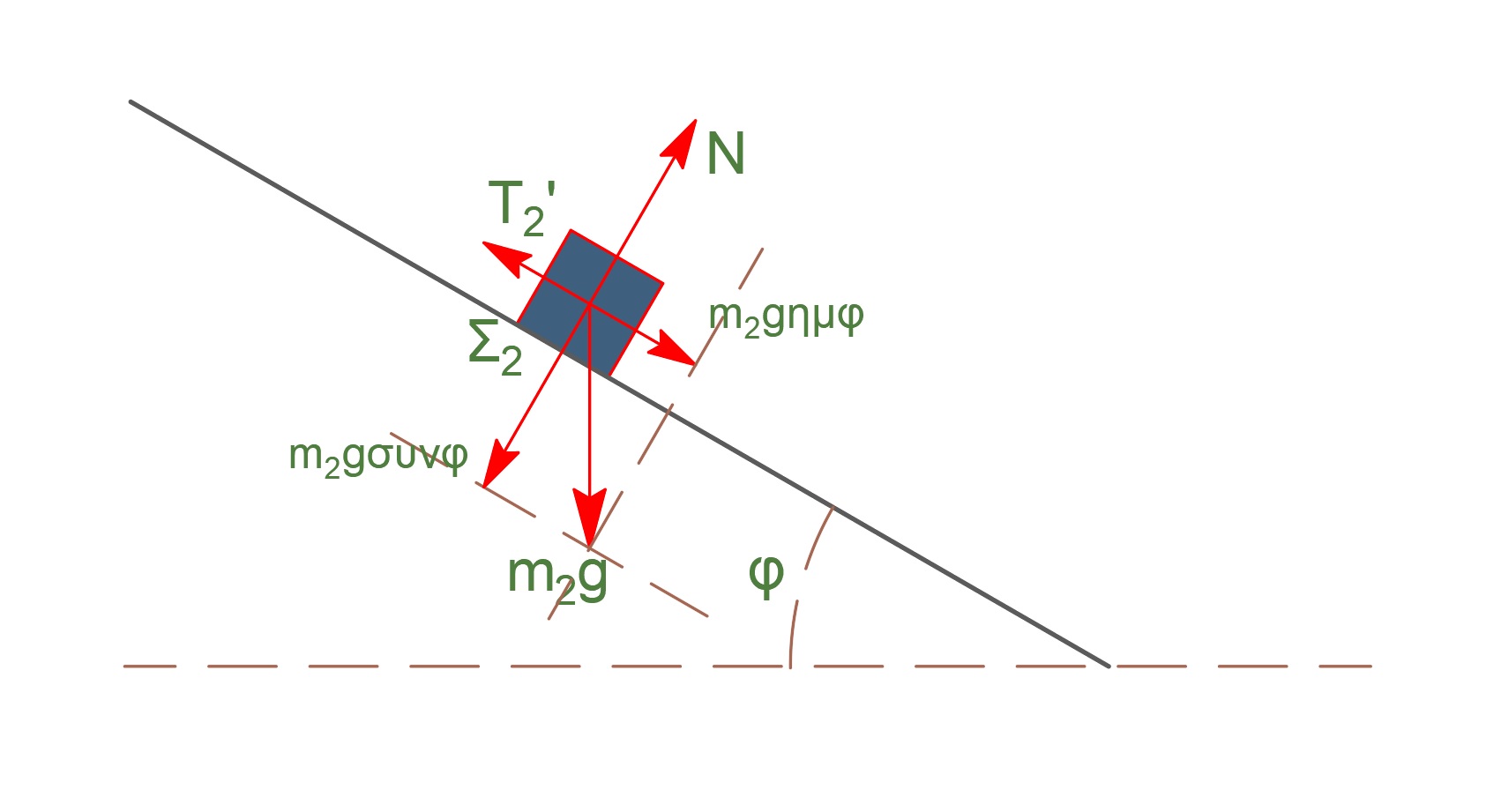
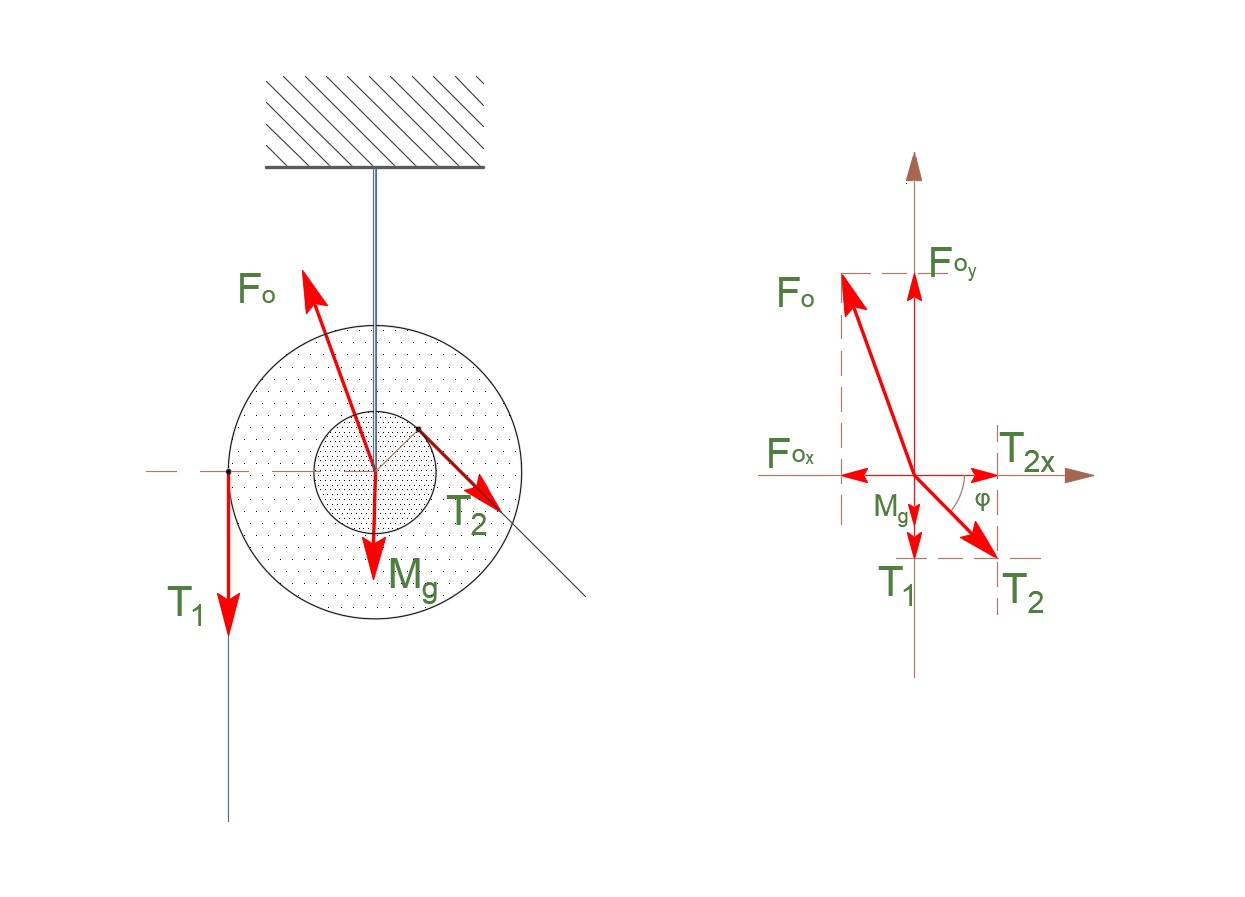
τροχαλία Τ: ισορροπία \(Σ\vec{τ_{(ο)}} = \vec0\)
\[\vec{τ_{Τ_1}} + \vec{τ_{Τ_2}} = \vec0 \Rightarrow T_1 \cdot r_1 = T_2 \cdot r_2 \Rightarrow T_1 = \frac{T_2}{2}\]τροχαλία Τ: ισορροπία \(Σ\vec{F_x} = \vec0\)
\[F_{ox} = T_{2x} \Rightarrow F_{ox} = T_2 \cdot συνφ\]τροχαλία Τ: ισορροπία \(Σ\vec{F_y} = \vec0\)
\[F_{oy} = T_1 + M \cdot g + T_2 \cdot ημφ\] \[β) \underline {τρόπος}\]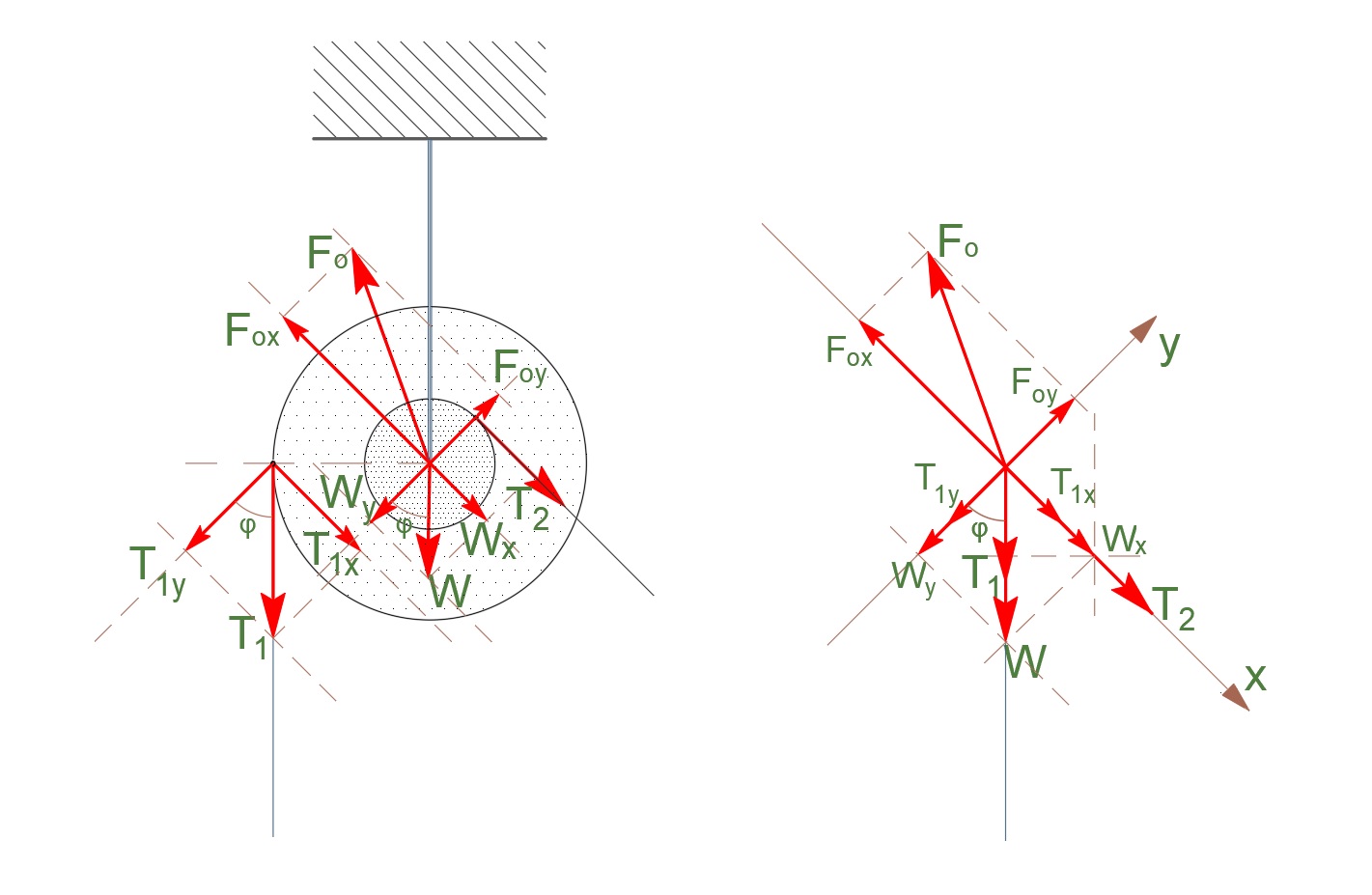
τροχαλία Τ: ισορροπία \(Σ\vec{τ_{(ο)}} = \vec0\)
\[\vec{τ_{Τ_1}} + \vec{τ_{Τ_2}} = \vec0 \Rightarrow T_1 \cdot r_1 = T_2 \cdot r_2 \Rightarrow T_1 = \frac{T_2}{2}\]τροχαλία Τ: ισορροπία \(Σ\vec{F_x} = \vec0\)
\[T_{1x} + W_x + T_2 = F_{ox} \Rightarrow T_1 \cdot ημφ + Μ \cdot g \cdot ημφ + Τ_2 = F_{ox}\]τροχαλία Τ: ισορροπία \(Σ\vec{F_y} = \vec0\)
\[F_{oy} = T_{1y} + W_y \Rightarrow F_{oy} = T_1 \cdot συνφ + Μ \cdot g \cdot συνφ\]και μετά τις πράξεις \(m_1 = 1.5kg \quad F_{ox} = 24N\) και \(F_{oy} = 48N\)
\[F_o = \sqrt{F_{ox}^2 + F_{oy}^2} \Rightarrow F_o = 24 \sqrt5 N\]Δ2-\((5)\)
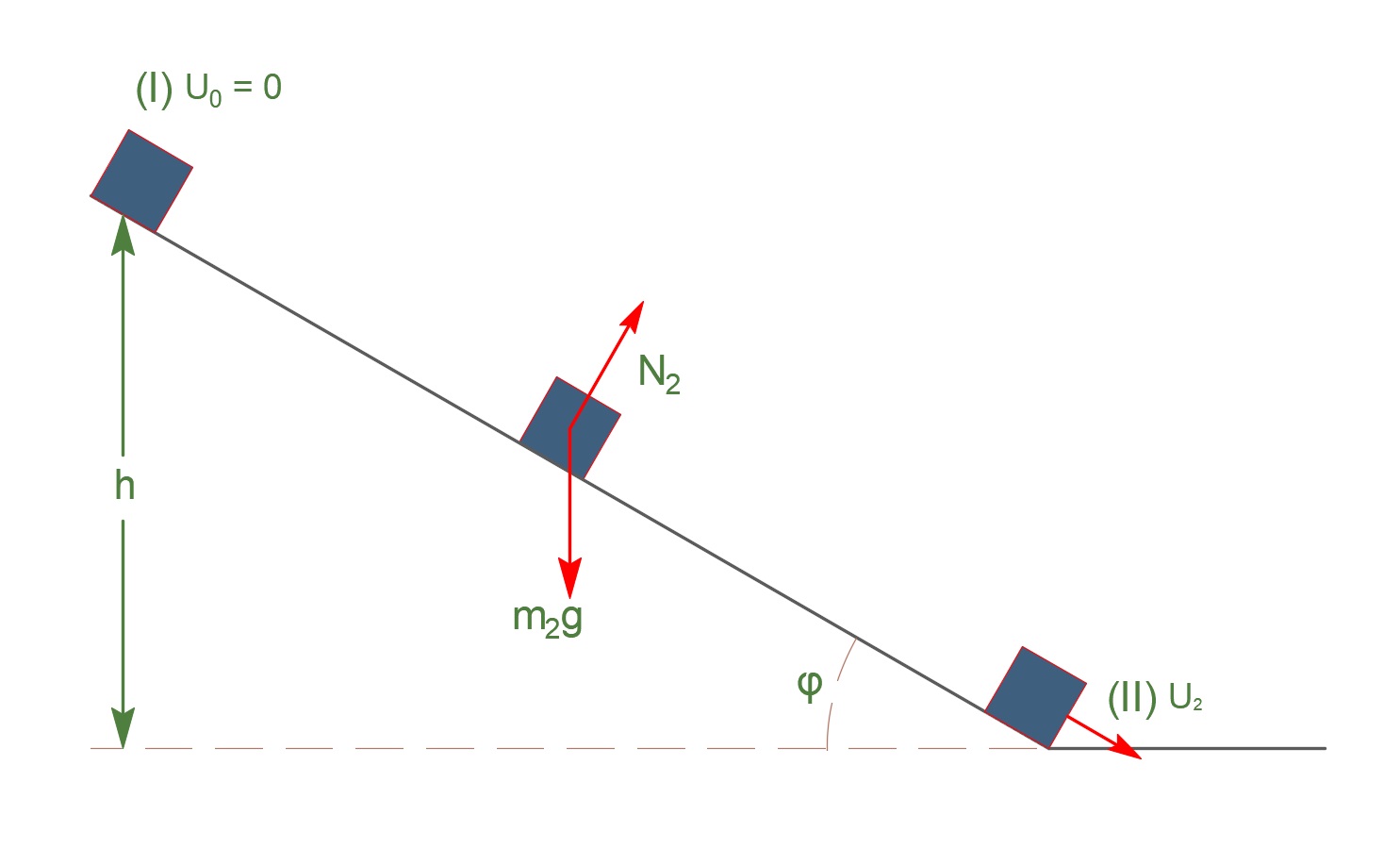
\(Σ_2:\) εξισώσεις κίνησης
\[ημφ = \frac{h}{x} \Rightarrow x = \frac{h}{ημφ}\] \[α = \frac{ΣF}{m_2} \Rightarrow α = \frac{W_x}{m_2} \Rightarrow α = g\cdot ημφ\] \[x = \frac{1}{2} \cdot α \cdot t^2 \Rightarrow t = \sqrt{\frac{2x}{α}} \Rightarrow t = \sqrt{\frac{2h}{g \cdot ημ^2φ}}\] \[υ = α \cdot t \Rightarrow υ_2 = \sqrt{2 \cdot g \cdot h} \Rightarrow υ_2 = 6 \frac{m}{s}\]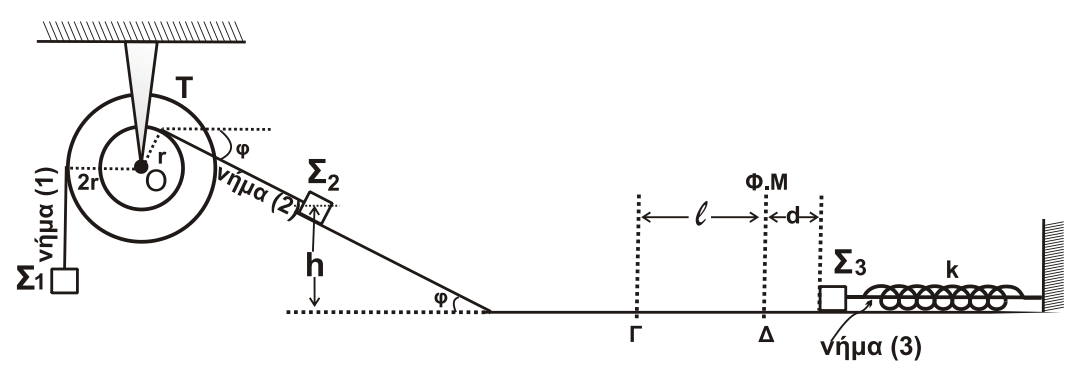
Δ3-\((5)\)
\[Θ.Ι. \equiv Θ.Φ.Μ. \Rightarrow υ_3 = υ_{max} = A \cdot ω \Rightarrow υ_3 = 1 \frac{m}{s}\]Κεντρική ελαστική κρούση, ίσες μάζες ανταλλαγή ταχυτήτων
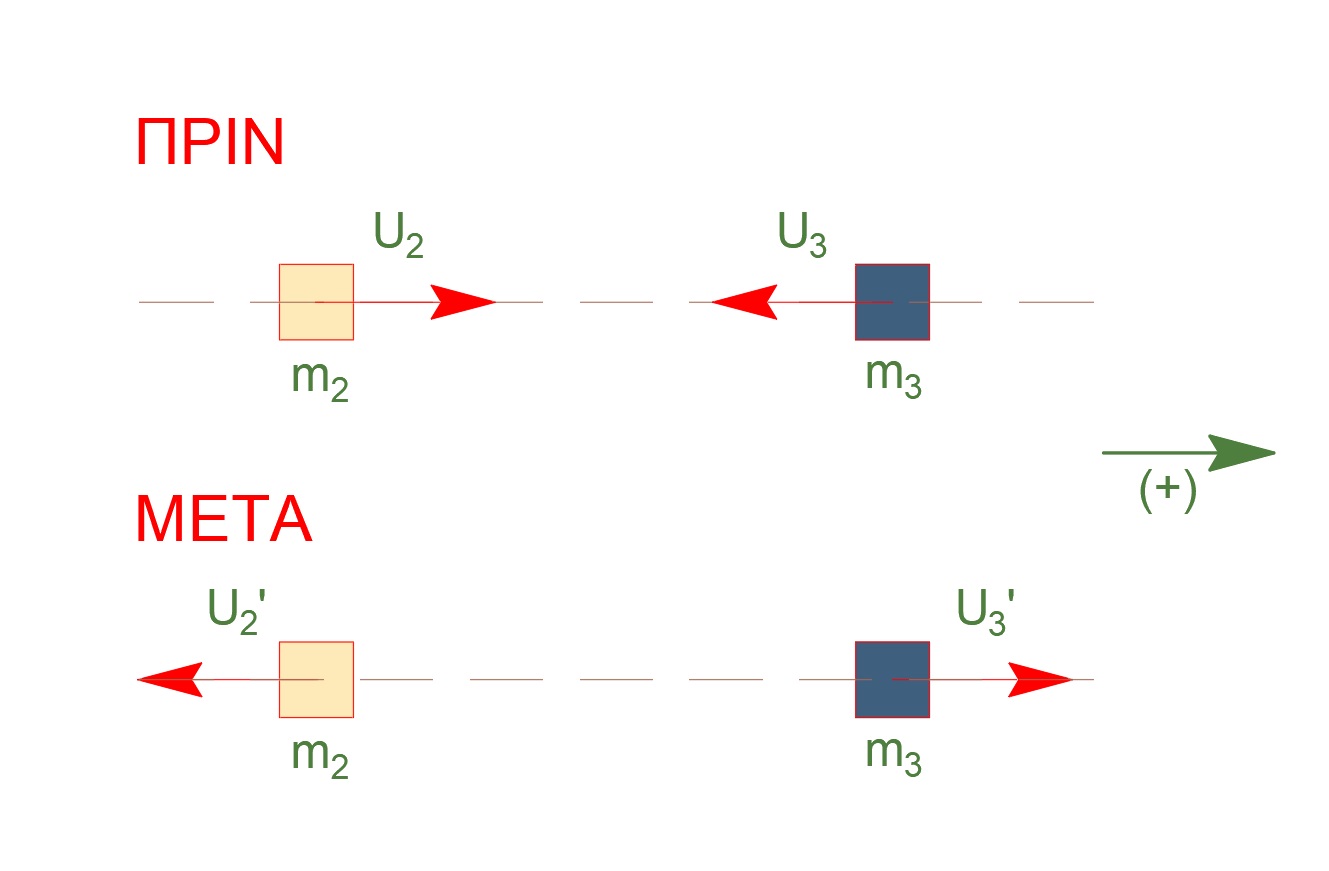
Δ4-\((6)\)
\[t_2: \quad K=8 \cdot U \quad E_{ταλ} = Κ + U \quad U = \frac{1}{2}\cdot k \cdot x^2\]Από Α.Δ.Ε.Τ. μετά τις πράξεις έχουμε: \(x = \pm 0.4m\)
\[x_Z = - 0.4m\]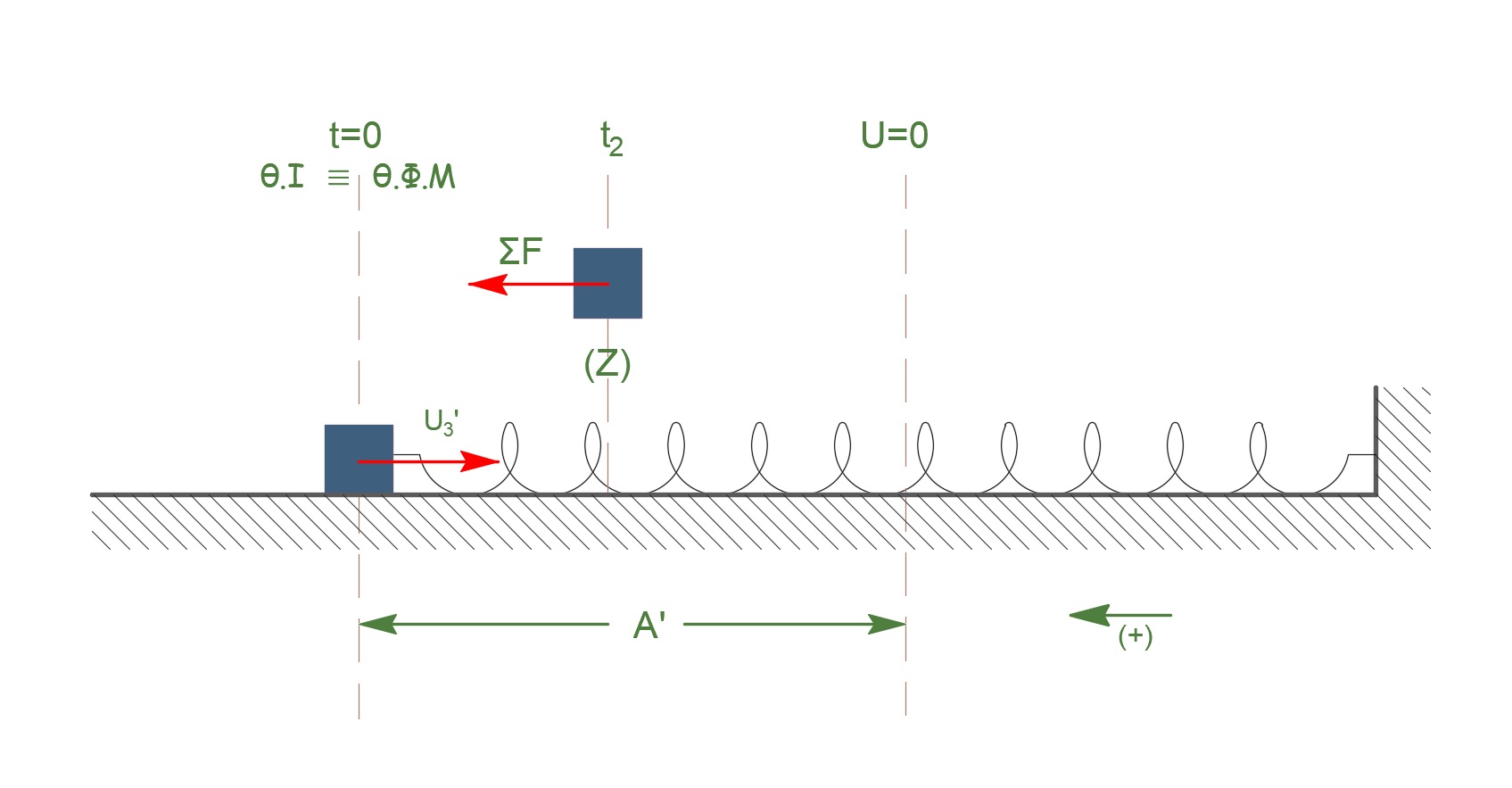
Από Α.Δ.Ε.Τ. μετά τις πράξεις έχουμε: \(υ = \sqrt{32} \frac{m}{s}\)
\[α) \underline {τρόπος}\] \[|\frac{ΔΚ}{Δt}| = |\frac{ΔW}{Δt}| = |ΣF \cdot υ \cdot συνφ|\]και μετά τις πράξεις \(\frac{ΔΚ}{Δt} = 200 \sqrt2 \frac{Joule}{s}\)
\[β) \underline {τρόπος}\] \[\frac{dK}{dt} = \frac{d}{dt}(\frac{1}{2} m υ^2) = \frac{1}{2}m \frac{d}{dt}(υ^2) = \frac{1}{2} m \cdot 2υ \frac{dυ}{dt}\] \[\frac{dK}{dt} = m \cdot υ \cdot α = -m_3 \cdot υ \cdot ω^2 \cdot x_Z\]και μετά τις πράξεις \(\frac{ΔΚ}{Δt} = 200 \sqrt2 \frac{Joule}{s}\)
Δ5-\((3)\)
Κεντρική ελαστική κρούση, ίσες μάζες ανταλλαγή ταχυτήτων
\[υ_2' = υ_3 \Rightarrow υ_2' = 1 \frac{m}{s}\]\(Θ.Ι. \equiv Θ.Φ.Μ.\) άρα για πρώτη φορά μετά την κρούση το \(Σ_3\) διέρχεται από την Θ.Φ.Μ. σε χρόνο:
\[Δt' = \frac{T}{2} \Rightarrow Δt' = 0.2π s\] \[Σ_2: Ε.Ο.Κ. \quad x = υ_2' \cdot Δt' \Rightarrow x = 0.628m\]Μπορείτε να εκτυπώσετε τα θέματα σε μορφή pdf από εδώ και τις λύσεις από εδώ
blog comments powered by Disqus