Ταλάντωση και βαρυτικό πεδίο

θέμα Γ

Από τον Νοέμβριο του 2000 υπάρχει συνεχής ανθρώπινη παρουσία στον Διεθνή Διαστημικό Σταθμό \((I.S.S.)\). Οι αστροναύτες δύο φορές κάθε εβδομάδα μετρούν την μάζα τους σε συνθήκες έλλειψης βαρύτητας.

Ο αστροναύτης Joe Acaba υπολογίζει τη μάζα του στο εργαστήριο του Columbus χρησιμοποιώντας συσκευή μέτρησης μάζας. Η φωτογραφία είναι από το αρχείο της NASA. (images.nasa.gov)

Η συσκευή που χρησιμοποιούν ονομάζεται \(SLAMMD\) (Space Linear Accelaration Mass Measurement Device). Αποτελείται από έναν βραχίονα προέκτασης που είναι προσαρτημένος στον Σταθμό με δύο ελατήρια. Ο κάθε αστροναύτης μάζας \(m_α\) προσδένει τον εαυτό του στον βραχίονα μάζας \(m_β\) και μετράει την περίοδο ταλάντωσης του βραχίονα.

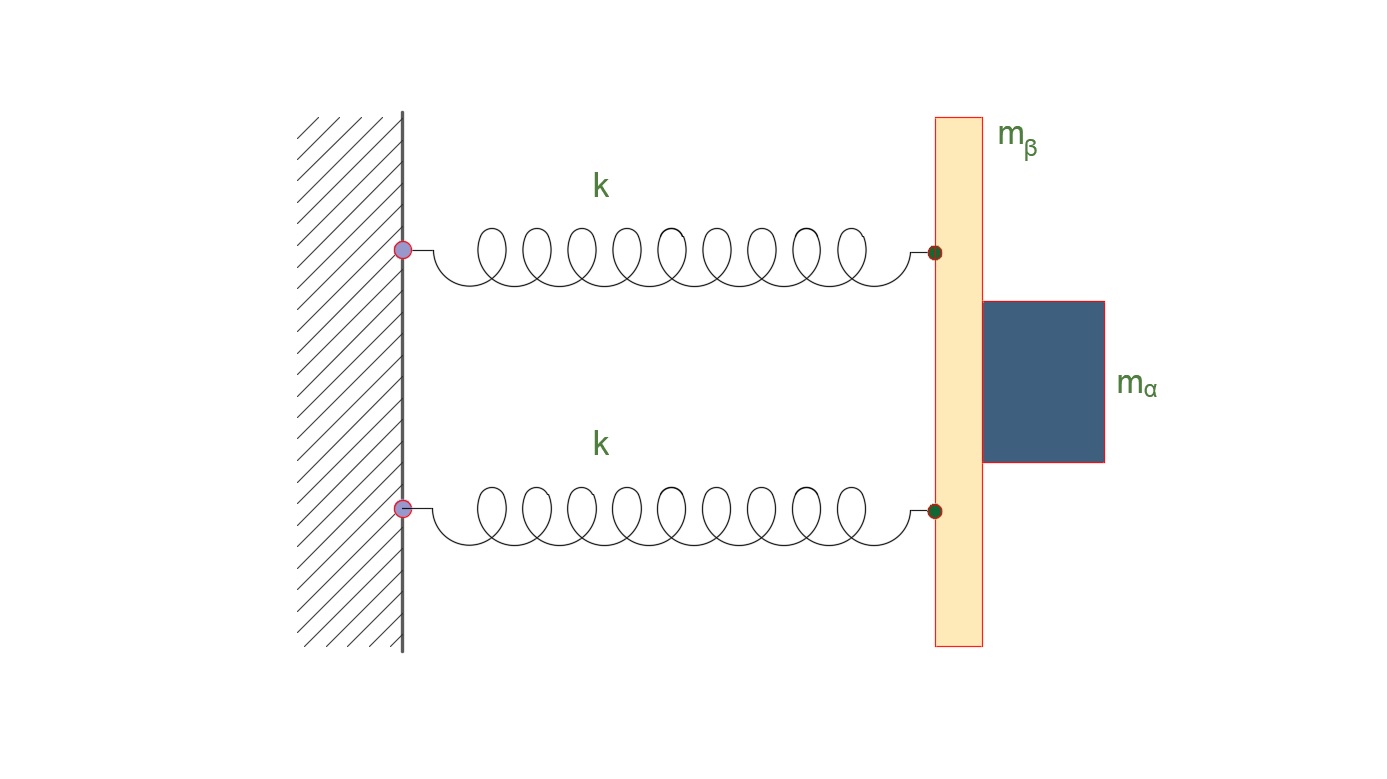
Γ1. Να υπολογίσετε την μάζα ενός μέλους του πληρώματος του \(I.S.S.\) αν γνωρίζετε την σταθερά κάθε ελατηρίου \(k = 300 \frac{N}{m}\), την περίοδο ταλάντωσης του βραχίονα \(SLAMMD\) χωρίς τον αστροναύτη \(1.0 s\) και την περίοδο ταλάντωσης με τον αστροναύτη \(2.4 s\).

Γ2. Να υπολογίσετε το μέτρο της επιτάχυνσης με την οποία κινείται ο \(I.S.S.\) αν γνωρίζετε την επιτάχυνση της βαρύτητας στην επιφάνεια της γης \(g_o = 10 \frac{m}{s^2}\), την ακτίνα της γης \(R_Γ = 6400 km\) και το ύψος του Σταθμού από την επιφάνεια της γης \(h = 400 km\). Θωρήστε ότι ο \(I.S.S.\) εκτελεί Ομαλή Κυκλική Κίνηση γύρω από το κέντρο της Γης.

Γ3. Η επόμενη γραφική παράσταση παρουσιάζει την ταχύτητα της μάζας ενός αστροναύτη σε συνάρτηση με την μετατόπιση από την θέση ισορροπίας του. Να υπολογίσετε το μέτρο της ταχύτητας ταλάντωσης του αστροναύτη, όταν αυτός διέρχεται από την θέση που απέχει \(Δl = 5 \cdot \sqrt3 \quad cm\) από την θέση ισορροπίας.

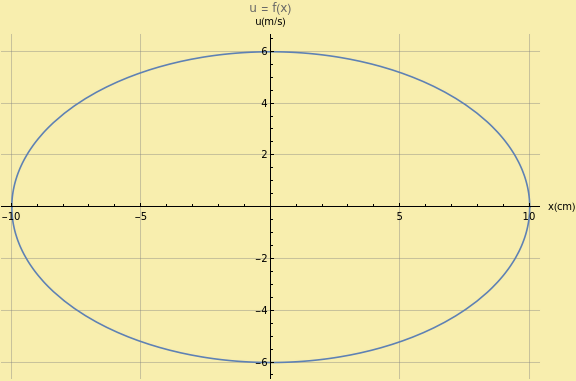
Δίνεται \(π^2 \simeq 10, \quad (\frac{16}{17})^2 \simeq 0,89\)

Ο κώδικας σε mathematica

			Plot[u/. Solve[(x/10)^2 + (u/6)^2 == 1], {x, -10, 10}, 
			Background -> LightBlue, 
 				PlotLabel -> "u = f(x)", 
 				GridLines -> Automatic,  
 				Background ->RGBColor[0.97,0.93,0.68],
 				AxesLabel -> {"x(cm)","u(m/s)"}, 
 				AxesStyle->Black, 
 				ImageSize->Large,
 				AspectRatio -> Automatic]

			Plot[2*Cos[10*t+Pi/2], {t, 0, Pi/5}, 
					PlotLegends ->"Expressions",  
					PlotRange -> All, 
					PlotLabel -> "\[CapitalDelta]\[Iota]\[Alpha]\[Kappa]\[Rho]ό\[Tau]\[Eta]\[Mu]\[Alpha]", 
					Background -> LightBlue, 
					GridLines -> Automatic, 
					AxesLabel -> {"t(s)", "x(cm)"}, 
                	Ticks ->{ {0, Pi/10, Pi/5}, {-3,3}},
					Filling -> Automatic]