Προσομοίωση 2021 - Β' Φάση 1ο ΓΕΛ Αλεξανδρούπολης, 2ο ΓΕΛ Καλαμαριάς, 11ο ΓΕΛ Θεσσαλονίκης, 27ο ΓΕΛ Θεσσαλονίκης, Αμερικάνικη Γεωργική σχολή, ΓΕΛ Λαγκαδά, ΓΕΛ Σοχού
ΘΕΜΑ A
Στις ερωτήσεις \(Α_1-Α_4\) να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την
ημιτελή πρόταση.
\(A_1\)
Σε σύστημα ελατηρίου - σώματος, εκτός από τη δύναμη επαναφοράς ενεργεί και δύναμη αντίστασης $F=-b\cdot υ$, όπου $b$ η σταθερά απόσβεσης και $υ$ η ταχύτητα του σώματος. Η σταθερά απόσβεσης εξαρτάται από:
- την ταχύτητα του σώματος που ταλαντώνεται
- την πυκνότητα και το μέγεθος του αντικειμένου που κινείται
- τις ιδιότητες του μέσου, το σχήμα και το μέγεθος του αντικειμένου που κινείται
- τις ιδιότητες του μέσου, την πυκνότητα και τον όγκο του αντικειμένου που κινείται
Μονάδες 5
\(A_2\)
Σύστημα ελατηρίου – μάζας εκτελεί εξαναγκασμένη ταλάντωση. Η συχνότητα του διεγέρτη είναι ίση με την ιδιοσυχνότητα του συστήματος. Αν τετραπλασιάσουμε τη μάζα στο σύστημα, τότε η ιδιοσυχνότητά του:
- γίνεται μέγιστη
- υποδιπλασιάζεται
- διπλασιάζεται
- υποτετραπλασιάζεται
Μονάδες 5
\(A_3\)
Ένα σώμα εκτελεί κίνηση που προέρχεται από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων, ίδιας διεύθυνσης, γύρω από το ίδιο σημείο, με εξισώσεις $x_1=Α_1 \cdot ημωt$ και $x_2 = A_2 \cdot ημ(ωt+φ)$. Η σύνθετη ταλάντωση που προκύπτει:
- έχει πλάτος $Α = \sqrt{A_1^2 + A_2^2 + 2 \cdot A_1 \cdot A_2}$
- έχει αρχική φάση $θ$ με $εφθ = \frac{A_2 \cdot ημφ}{Α_1+Α_2 \cdot συνφ}$
- έχει ενέργεια ίση με το άθροισμα των ενεργειών των επιμέρους ταλαντώσεων
- έχει εξίσωση της μορφής $x = A' \cdot ημωt$
Μονάδες 5
\(A_4\)
Δύο μικρά σώματα συγκρούονται μετωπικά και πλαστικά. Ο λόγος της ολικής κινητικής ενέργειας του συστήματος των μαζών πριν και μετά την κρούση είναι $\frac{K_{ολ}^{μετά}}{Κ_{ολ}^{πριν}} = 0.75$ Το ποσοστό της κινητικής ενέργειας που μετατράπηκε σε θερμότητα κατά την κρούση είναι:
- 0 %
- 25 %
- 50 %
- 75 %
Μονάδες 5
\(Α_5\)
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
- Το έργο της δύναμης που προκαλεί την απόσβεση σε μια φθίνουσα μηχανική ταλάντωση είναι πάντα θετικό.
- Καθώς τα αμορτισέρ του αυτοκινήτου παλιώνουν και φθείρονται, η τιμή του b ελαττώνεται και η ταλάντωση διαρκεί περισσότερο.
- Ένα σώμα εκτελεί κίνηση που προέρχεται από την σύνθεση των εξής απλών αρμονικών ταλαντώσεων $$y_1 = 0.1 \cdot ημ10t \ (SI) \qquad y_2 = 0.2 \cdot ημ(10t+\pi) \ (SI)$$ Αν οι δυο ταλαντώσεις εξελίσονται στην ίδια διεύθυνση και γύρω από την ίδια θέση ισορροπίας τότε η φάση της σύνθετης ταλάντωσης είναι $$φ = 10t + \pi \ (SI)$$
- Σε μια κρούση αμελητέας χρονικής διάρκειας η δυναμική ενέργεια των σωμάτων, που εξαρτάται από τη θέση τους στο χώρο, δεν μεταβάλλεται
- Σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις, ίδιου πλάτους Α, ίδιας διεύθυνσης και μηδενικής αρχικής φάσης, γύρω από την ίδια θέση ισορροπίας. Αν οι δύο ταλαντώσεις έχουν συχνότητες οι οποίες διαφέρουν λίγο μεταξύ τους τότε η συνισταμένη ταλάντωση του συστήματος είναι απλή αρμονική.
Μονάδες 5
ΘΕΜΑ Β
\(Β_1\)
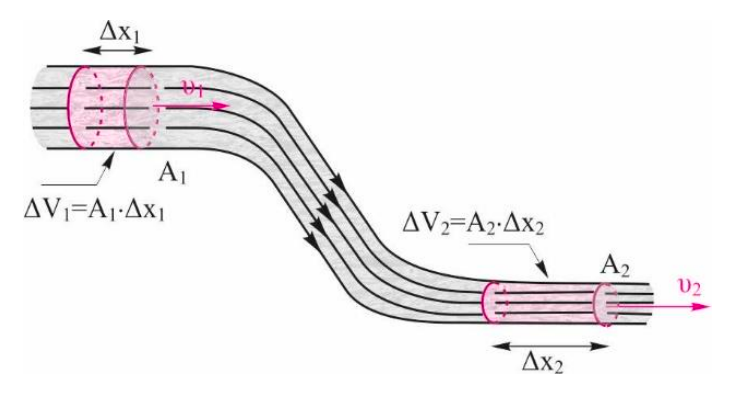
Για μια ποσότητα \(Δm\) ιδανικού ρευστού που κατέρχεται σε σωλήνα, του οποίου η διατομή ελαττώνεται κατά την φορά της ροής του ρευστού, γνωρίζουμε ότι τα μέτρα των μεταβολών της δυναμικής και της κινητικής ενέργειας ανά μονάδα όγκου είναι αντίστοιχα \(30 \frac{J}{L}\) και \(70 \frac{J}{L}\)
- Η ποσότητα $Δm$ του ιδανικού ρευστού δέχεται από το περιβάλλον, λόγω διαφοράς πίεσης, ενέργεια ανά μονάδα όγκου $100 \frac{J}{L}$
- Η ποσότητα $Δm$ του ιδανικού ρευστού προσφέρει στο περιβάλλον, λόγω διαφοράς πίεσης, ενέργεια ανά μονάδα όγκου $40 \frac{J}{L}$
- Το περιβάλλον ρευστό προσφέρει στην ποσότητα $Δm$, λόγω διαφοράς πίεσης, ενέργεια ανά μονάδα όγκου $40 \frac{J}{L}$
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση
Μονάδες 2
Να αιτιολογήσετε την απάντησή σας
Μονάδες 7
\(Β_2\)
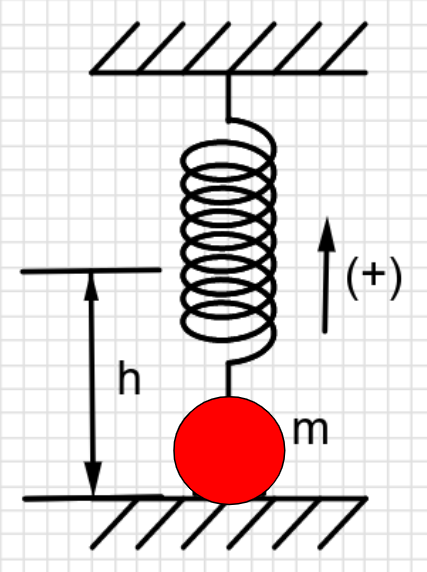
Η σφαίρα μάζας $m$ ισορροπεί σε οριζόντιο επίπεδο και είναι δεμένη στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς $k$, που σε αυτή τη θέση έχει το φυσικό του μήκος. Ανυψώνουμε την σφαίρα κατά $h = \frac{3mg}{7k}$ και τη χρονική στιγμή $t = 0$ την αφήνουμε ελεύθερη. Η σφαίρα συγκρούεται ελαστικά με το δάπεδο. Ο χρόνος $Δt$ που μεσολαβεί μεταξύ δύο διαδοχικών κρούσεων της σφαίρας με το δάπεδο είναι:
- $$\frac{π}{3} \cdot \sqrt{\frac{m}{k}}$$
- $$\frac{π}{2} \cdot \sqrt{\frac{m}{k}}$$
- $$\frac{π}{4} \cdot \sqrt{\frac{m}{k}}$$
Δίνεται $ημ\frac{π}{4} = 0.7$
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση
Μονάδες 2
Να αιτιολογήσετε την απάντησή σας
Μονάδες 6
\(Β_3\)
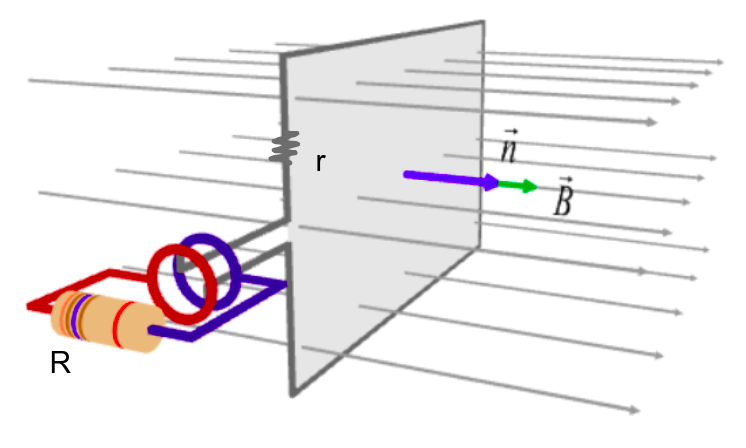
Συρμάτινο πλαίσιο αντίστασης $r = \frac{R}{2}$ στρέφεται μέσα σε ομογενές μαγνητικό πεδίο έντασης $Β$ με σταθερή γωνιακή ταχύτητα $ω$. Τα άκρα του πλαισίου συνδέονται με αντιστάτη ωμικής αντίστασης $R_1 = 2R$. Στο χρονικό διάστημα $Δt_1$, που το πλαίσιο έχει εκτελέσει $N_1$ στροφές, στον αντιστάτη $R_1$ εκλύεται θερμότητα $Q_1$. Στη συνέχεια συνδέουμε παράλληλα με τον πρώτο αντιστάτη, δεύτερο αντιστάτη ωμικής αντίστασης $R_2 = 2R$ και το συρμάτινο πλαίσιο στρέφεται μέσα στο ίδιο μαγνητικό πεδίο με την ίδια γωνιακή ταχύτητα. Στον αντιστάτη $R_1$ για χρονικό διάστημα $Δt_2$, που το πλαίσιο έχει εκτελέσει $Ν_2$ στροφές εκλύεται πάλι η ίδια ποσότητα θερμότητας $Q_2=Q_1$. Ο λόγος $\frac{N_1}{N_2}$ είναι ίσος με:
- $$\frac{25}{36}$$
- $$\frac{25}{9}$$
- $$\frac{36}{25}$$
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση
Μονάδες 2
Να αιτιολογήσετε την απάντησή σας
Μονάδες 6
ΘΕΜΑ Γ
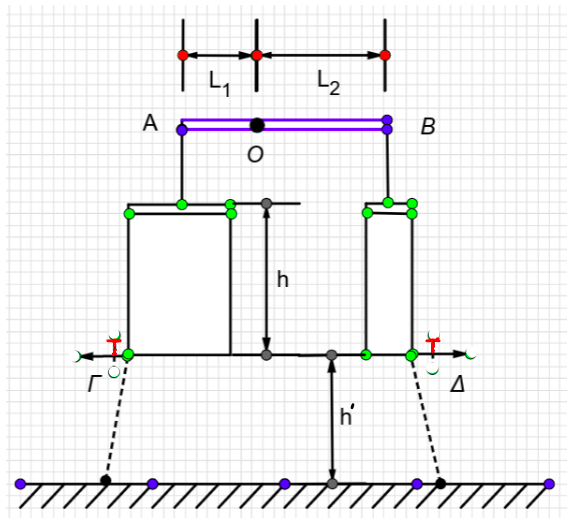
Ομογενής ράβδος \(ΑΒ\) μήκους $L=30cm$ και μάζας $Μ = 20kg$ μπορεί να στρέφεται χωρίς τριβές, γύρω από οριζόντιο άξονα στήριξης που διέρχεται από το σημείο της $Ο$ και ισορροπεί ακίνητη οριζόντια όπως φαίνεται στο παραπάνω σχήμα. Τα άκρα $Α$ και $Β$ της ράβδου, απέχουν από το σημείο $Ο$ αποστάσεις $L_1$ και $L_2$ τέτοιες ώστε $L_2 = 2 \cdot L_1$, ενώ είναι δεμένα με αβαρή και μη εκτατά νήματα με τα κέντρα δύο εμβόλων με τετράγωνο προφίλ και πλευρές $α_1 = 10 cm$ και $α_2 = 5 cm$ αντίστοιχα. Τα τετραγωνικά έμβολα με μάζες $m_1 = 24 kg$ και $m_2 = 20 kg$, μπορούν να κινούνται χωρίς τριβές και κλείνουν αεροστεγώς τα τετράγωνα δοχεία που είναι γεμάτα με νερό πυκνότητας $ρ = 1 \frac{g}{cm^3}$. Το ύψος του νερού σε κάθε δοχείο είναι $h = 30cm$, η ατμοσφαιρική πίεση $p_{ατμ} = 10^5 \frac{N}{m^2}$, η επιτάχυνση της βαρύτητας $g = 10 \frac{m}{s^2}$ και η συνολική δύναμη που δέχεται ο πυθμένας του δοχείου με εμβαδόν διατομής $Α_2$ είναι $F_2 = 375 Ν$. Τα δύο δοχεία είναι τοποθετημένα σε τραπέζι ύψους $h’ = 20 cm$ από το έδαφος. Υποθέστε ότι το εμβαδόν διατομής του κάθε δοχείου είναι ίσο με το εμβαδόν διατομής του αντίστοιχου τετραγωνικού εμβόλου.
\(Γ_1\)
Να υπολογίσετε το μέτρο της δύναμης που δέχεται η ράβδος στο σημείο $Ο$ από τον οριζόντιο άξονα στήριξης.
Μονάδες 6
\(Γ_2\)
Να υπολογίσετε την δύναμη που δέχεται το έμβολο διατομής $A_1$ από το νερό.
Μονάδες 6
\(Γ_3\)
Την χρονική στιγμή $t=0$ ανοίγουμε ταυτόχρονα τις δύο βάνες στα σημεία $Γ$ και $Δ$ που βρίσκονται στους πυθμένες των δοχείων, προσαρμοσμένες σε οπές με εμβαδόν διατομής $Α = 1 cm^2$. Να υπολογίσετε την απόσταση μεταξύ των δύο σημείων που οι φλέβες του νερού των δύο δοχείων συναντούν για πρώτη φορά το έδαφος.
Μονάδες 6
\(Γ_4\)
Να υπολογίσετε τους ρυθμούς μεταβολής της κινητικής ενέργειας για κάθε στοιχειώδη ποσότητα ρευστού την στιγμή που η κάθε φλέβα νερού εξέρχεται από την κάθε βάνα.
Μονάδες 7
ΘΕΜΑ Δ
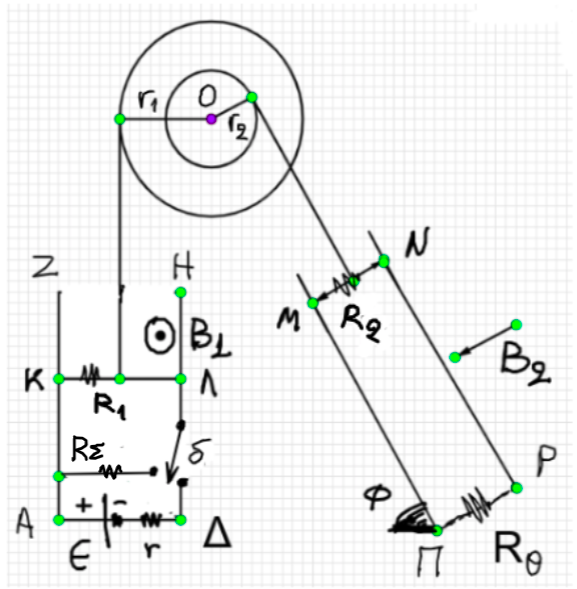
Η διπλή αβαρής τροχαλία του παραπάνω σχήματος μπορεί να περιστρέφεται χωρίς τριβές γύρω από
οριζόντιο άξονα $Ο$ και έχει εξωτερική ακτίνα $r_1 = 10 cm$ και εσωτερική ακτίνα $r_2 = 5 cm$.
Η τροχαλία έχει αμελητέα μάζα, δηλαδή κάθε στιγμή ισχύει για αυτήν ότι το άθροισμα
των ροπών που της ασκούνται ως προς τον άξονα περιστροφής της $Ο$ είναι ίσο με μηδέν,
είτε ισορροπεί, είτε κινείται. Γύρω από τις δύο αύλακες της τροχαλίας είναι τυλιγμένα αβαρή μη εκτατά νήματα στα άκρα των
οποίων είναι δεμένες δύο μεταλλικές ράβδοι $ΚΛ$ και $ΜΝ$ μήκους $L = 0.5 m$
Η πρώτη μεταλλική ράβδος έχει μάζα $m_1 = 1kg$, αντίσταση $R_1 = 5Ω$ και μπορεί να ολισθαίνει χωρίς τριβές πάνω στους
κατακόρυφους αγωγούς $ΖΑ$ και $ΗΔ$ άπειρου μήκους. Όταν ο μεταγωγός $δ$ είναι κατακόρυφος δημιουργεί
το ηλεκτρικό κύκλωμα $ΚΑΔΛΚ$ το οποίο βρίσκεται σε οριζόντιο ομογενές μαγνητικό πεδίο μέτρου
$Β_1 = 2 Τ$. Οι αγωγοί $ΖΑ$ και $ΗΔ$ έχουν αμελητέα ωμική αντίσταση και η ηλεκτρική πηγή έχει
ηλεκτρεργερτική δύναμη $Ε=30V$ και εσωτερική αντίσταση $r=1Ω$.
Η δεύτερη μεταλλική ράβδος έχει μάζα $m_2$, αντίσταση $R_2 = 3Ω$ και μπορεί να ολισθαίνει χωρίς τριβές πάνω στους
αγωγούς $ΜΠ$ και $ΝΡ$ επίσης άπειρου μήκους, που σχηματίζουν γωνία $φ=30^ο$ με τον ορίζοντα.
Οι αγωγοί συνδέονται με θερμαντική συσκευή ωμικής αντίστασης $R_θ$ με κανονικά στοιχεία
λειτουργίας $9V/27W$. Tο ηλεκτρικό κύκλωμα $MNPΠM$ βρίσκεται σε ομογενές μαγνητικό πεδίο μέτρου
$Β_2 = 2 Τ$ κάθετο στο επίπεδό του, όπως φαίνεται στο σχήμα. Οι αγωγοί $ΜΠ$ και $ΝΡ$ έχουν αμελητέα ωμική αντίσταση.
\(Δ_1\)
Αν γνωρίζετε ότι το σύστημα της διπλής τροχαλίας και των δύο μεταλλικών αγωγών ισορροπεί
ακίνητο να επαληθεύσετε ότι η μάζα του μεταλλικού αγωγού $ΜΝ$ είναι $m_2 = 6kg$.
Μονάδες 6
\(Δ_2\)
Την χρονική στιγμή $t=0$ ο μεταγωγός $δ$ αλλάζει ακαριαία θέση και συνδέεται με την ωμική αντίσταση $R_Σ = 1Ω$, έτσι ώστε το κύκλωμα δεν περιλαμβάνει πλέον την ηλεκτρική πηγή. Στην πρώτη μεταλλική ράβδο $ΚΛ$ ασκείται δύναμη από την τάση του νήματος με κατεύθυνση κατακόρυφα προς τα πάνω, ενώ στην δεύτερη $ΜΝ$ ασκείται συνισταμένη δύναμη (συνιστώσα του βάρους και τάση του νήματος) με διεύθυνση την διεύθυνση του πλάγιου επιπέδου και φορά προς τα κάτω. Να υπολογίσετε την επιτάχυνση της κάθε μεταλλικής ράβδου την χρονική στιγμή $t=0$.
Μονάδες 4
\(Δ_3\)
Να υπολογίσετε την οριακή ταχύτητα που αποκτά η κάθε μία μεταλλική ράβδος.
Μονάδες 8
\(Δ_4\)
Να εξετάσετε αν η θερμαντική συσκευή αντίστασης $R_θ$ λειτουργεί κανονικά και να υπολογίσετε όταν οι ράβδοι $ΚΛ$ και $ΜΝ$ κινούνται με τίς οριακές ταχύτητες τους παρακάτω ρυθμούς μεταβολής για κάθε ράβδο:
-
Ρυθμός μεταβολής της βαρυτικής δυναμικής ενέργειας.
-
Ισχύς της δύναμης του βάρους.
-
Ισχύς που παρέχει η κάθε ηλεκτρεργερτική δύναμη στο κύκλωμά της.
-
Ίσχύς της δύναμης $Laplace$.
-
Ρυθμός παραγωγής θερμότητας σε κάθε κύκλωμα.
-
Ρυθμός μεταβολής της κινητικής ενέργειας κάθε ράβδου.
Τέλος να επαληθεύσετε ότι ο συνολικός ρυθμός παραγωγής θερμότητας και στα δύο κυκλώματα ισούται με τον συνολικό ρυθμό μεταβολής της βαρυτικής δυναμικής ενέργειας των δύο ραβδών.
Μονάδες 7
Υπολογισμός ρυθμού μεταβολής στοιχειώδους μάζας ρευστού
πυκνότητα x παροχή = ρυθμός μεταβολής της μάζας
\[ρ \cdot Π = \frac{dm}{dV} \cdot \frac{dV}{dt} = \frac{dm}{dt}\]α) τρόπος
μεταβάλλεται η μάζα και είναι σταθερή η ταχύτητα.
(study4exams Επαναληπτικά θέματα - Κεφάλαιο 3 - Επαναληπτικά προβλήματα - Θέμα Δ - Πρόβλημα 5)
\[\frac{dK}{dt} = \frac{d(\frac{1}{2}m \cdot υ^2)}{dt} = \frac{1}{2}υ^2 \cdot \frac{dm}{dt} = \frac{1}{2} \cdot ρ \cdot Π \cdot υ^2\]β) τρόπος
μεταβάλλεται η ταχύτητα και είναι σταθερή η μάζα.
(study4exams Κεφάλαιο 3 Ρευστά σε κίνηση - Ενότητα 2 - Θέματα προς επίλυση - Ερωτήσεις Θεωρίας - θέμα Β - Ερώτηση 3)
Η στοιχειώδη μάζα λίγο πριν την έξοδο από το δοχείο έχει ταχύτητα σχεδόν μηδέν και λίγο μετά έχει σταθερή ταχύτητα $υ$.
\[\frac{dK}{dt} = \frac{d(\frac{1}{2}m \cdot υ^2)}{dt} = \frac{1}{2}m \cdot \frac{d(υ^2)}{dt} = \frac{1}{2} m \cdot 2υ \cdot \frac{dυ}{dt} = m \cdot υ \cdot α\] \[\frac{dK}{dt} = F \cdot υ = \frac{dP}{dt} \cdot υ = \frac{dm \cdot υ}{dt} \cdot υ = \frac{ρ \cdot dV \cdot υ}{dt} \cdot υ = ρ \cdot Π \cdot υ^2\]γ) τρόπος
μεταβάλλεται και η μάζα και η ταχύτητα
\[\frac{dK}{dt} = \frac{d(\frac{1}{2}m \cdot υ^2)}{dt} = \frac{1}{2}υ^2 \cdot \frac{dm}{dt} +\frac{1}{2}m \cdot \frac{dυ^2}{dt} = \frac{3}{2} \cdot ρ \cdot Π \cdot υ^2\]blog comments powered by Disqus