Διαγώνισμα στο στερεό με την νέα ύλη
**ΘΕΜΑ A (30Μ) **
Στις ερωτήσεις \(Α_1-Α_4\) να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση.
\(A_1\)
Σε ένα αρχικά ακίνητο στερεό σώμα ασκούνται ομοεπίπεδες δυνάμεις έτσι ώστε αυτό να εκτελεί μόνο επιταχυνόμενη μεταφορική κίνηση. Για τη συνισταμένη των δυνάμεων \(\sum \vec F\) που του ασκούνται και για το αλγεβρικό άθροισμα των ροπών \(\sum \vec τ\) ως προς το κέντρο μάζας του στερεού, ισχύει:
- $$ \sum \vec F = 0, \quad \sum \vec τ = 0$$
- $$ \sum \vec F \neq 0, \quad \sum \vec τ \neq 0$$
- $$ \sum \vec F \neq 0, \quad \sum \vec τ = 0$$
- $$ \sum \vec F = 0, \quad \sum \vec τ \neq 0$$
\(A_2\)
Η περίοδος περιστροφής της Γης γύρω από τον άξονά της είναι σταθερή. Αυτό οφείλεται στο ότι η ελκτική δύναμη που δέχεται η Γη από τον Ήλιο
- δημιουργεί σταθερή ροπή (διάφορη του μηδενός) ως προς τον άξονά της.
- δημιουργεί μηδενική ροπή ως προς τον άξονά της.
- έχει τη διεύθυνση της εφαπτομένης, μόνο σε ένα σημείο του Ισημερινού της Γης.
- είναι τόσο μικρή που δεν επηρεάζει την περιστροφή της Γης.
\(A_3\)
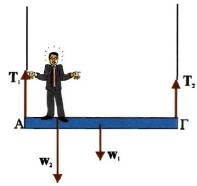
Οριζόντια ομογενής δοκός μήκους \(L\) και βάρους \(w_1\), κρέμεται από δύο αβαρή μη εκτατά νήματα που είναι δεμένα στις άκρες της. Ένας άνθρωπος (θεωρείται υλικό σημείο) βάρους \(w_2 = 2 \cdot w_1\), βρίσκεται σε απόσταση \(d = \frac{L}{4}\) από το άκρο \(Α\) της δοκού. Ο λόγος των μέτρων \(\frac{Τ_1}{Τ_2}\) των τάσεων των νημάτων που ασκούνται στη δοκό είναι:
\[α. 1 \quad β. \frac{1}{2} \quad γ. 2 \quad δ. \frac{3}{2}\]\(A_4\)
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
α. Ένα ελεύθερο στερεό στο οποίο ασκείται ζεύγος δυνάμεων εκτελεί σύνθετη κίνηση.
β. Ένα στερεό που στρέφεται γύρω από ακλόνητο άξονα με σταθερή γωνιακή ταχύτητα, λέμε ότι ισορροπεί.
γ. Αν σε ένα ελεύθερο στερεό η συνισταμένη δύναμη είναι μηδέν, τότε η συνολική ροπή ως προς το κέντρο μάζας είναι πάντοτε μηδέν.
δ. Η μονάδα της ροπής δύναμης στο S.I. είναι το \(1 \frac{N}{m}\).
ε. Η ροπή που προκαλεί μια δύναμη εξαρτάται από την κάθετη απόσταση της δύναμης από τον άξονα περιστροφής (μοχλοβραχίονας).
**ΘΕΜΑ Β (30Μ) **
\(Β_1\)
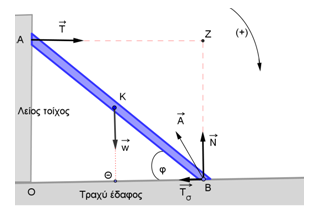
Το ένα άκρο αβαρούς σκάλας \(AB\) μήκους \(L = 5m\), ακουμπάει σε λείο κατακόρυφο τοίχο και απέχει κατακόρυφη απόσταση \(AO = 4m\) από το οριζόντιο τραχύ δάπεδο με το οποίο έρχεται σε επαφή το άλλο άκρο της \(B\). Για να καταφέρει ένα μικρό παιδί βάρους \(\vec w\) (που θεωρείται υλικό σημείο \(K\)) να ανέβει τη σκάλα, η ελάχιστη τιμή του συντελεστή στατικής τριβής της σκάλας με το οριζόντιο δάπεδο είναι:
\[α. μ_σ = 0.25 \quad β. μ_σ = 0.5 \quad γ. μ_σ = 0.75\]Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
\(Β_2\)
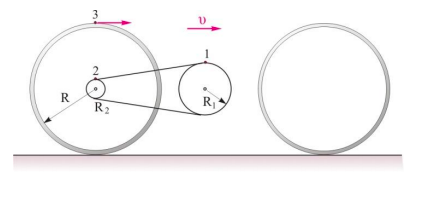
Ένα ποδήλατο κινείται ευθύγραμμα και ομαλά σε οριζόντιο έδαφος με τους τροχούς του να κυλίονται. Ο μεγάλος δίσκος στον οποίο είναι προσαρμοσμένα τα πετάλια έχει ακτίνα \(R_1\) και εκτελεί \(120\) στροφές το λεπτό. Ο μικρός δίσκος, ο οποίος είναι στερεωμένος στον τροχό, έχει ακτίνα \(R_2 = \frac{R_1}{3}\). Αν ο τροχός του ποδηλάτου έχει ακτίνα \(R = \frac{5}{4π} m\), τότε η ταχύτητα του ποδηλάτου έχει μέτρο
\[α. 0.6π \frac{m}{s} \quad β. 15 \frac{m}{s} \quad γ. 6 \frac{m}{s}\]Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
\(Β_3\)
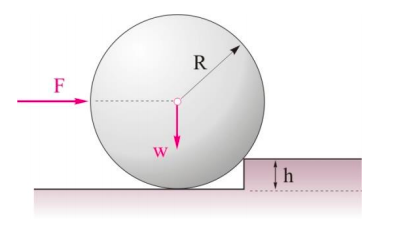
Στο παραπάνω σχήμα, ο τροχός έχει ακτίνα \(R\) και βάρος \(w\). Το εμπόδιο έχει ύψος \(h = \frac{R}{3}\). Ασκούμε στον τροχό στην οριζόντια διεύθυνση δύναμη μέτρου \(F\), της οποίας ο φορέας διέρχεται από το κέντρο μάζας του τροχού. Ο τροχός χάνει την επαφή με το δάπεδο και υπερπηδά το εμπόδιο, όταν το μέτρο της δύναμης \(F\), είναι
- $$ F \geq \frac{\sqrt5}{2} \cdot w $$
- $$ F \geq \sqrt5 \cdot w $$
- $$ F \geq \sqrt2 \cdot w$$
Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
**ΘΕΜΑ Γ (40Μ) **
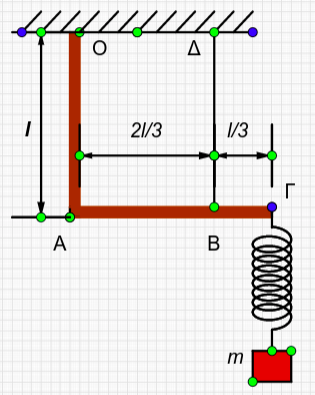
Δύο άκαμπτοι ομογενείς ράβδοι \(ΑΓ\) και \(ΑΟ\) με μήκη \(ΑΓ = ΑΟ = l = 3 m\) συγκολλούνται στο \(Α\) έτσι ώστε να είναι κάθετοι μεταξύ τους. Στο άκρο \(Ο\) υπάρχει άρθρωση και το σύστημα των δύο ράβδων μπορεί να στρέφεται χωρίς τριβές γύρω από το \(Ο\) σε κατακόρυφο επίπεδο. Στο σημείο \(Β\) που απέχει \(\frac{l}{3}\) από το άκρο \(Γ\), έχουμε δέσει κατακόρυφο νήμα \(ΒΔ\), ενώ στο σημείο \(Γ\) το ένα άκρο ιδανικού ελατηρίου σταθεράς \(k = 100 \frac{N}{m}\) στο άλλο άκρο του οποίου είναι δεμένο σώμα \(Σ\) μάζας \(m = 1 kg\) Το όλο σύστημα ισορροπεί. Δίνεται η επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\) και η μάζα κάθε ράβδου \(Μ_{ΑΓ} = Μ_{ΑΟ} = 4 kg\).
\(Γ_1\) Να υπολογίσετε την τάση του νήματος
Το όριο θραύσης του νήματος είναι \(Τ_θ = 120Ν\). Μετατοπίζουμε το σώμα \(Σ\) προς τα κάτω κατά \(Δl = 0.2m\) και την χρονική στιγμή \(t=0\) το αφήνουμε ελεύθερο να κινηθεί. Θεωρήστε ότι το σώμα \(Σ\) εκτελεί απλή αρμονική ταλάντωση.
\(Γ_2\) Να γράψετε την εξίσωση της απομάκρυνσης σαν συνάρτηση του χρόνου, θεωρώντας θετική φορά την προς τα πάνω.
\(Γ_3\) Να σχεδιάσετε σε κατάλληλα βαθμολογημένους άξονες τη γραφική παράσταση της τάσης του νήματος συναρτήσει της απομάκρυνσης του σώματος \(Σ\) από τη θέση ισορροπίας του.
\(Γ_4\) Υπολογίστε το μέγιστο πλάτος ταλάντωσης, έτσι ώστε το νήμα να μη χαλαρώνει αλλά ούτε να κινδυνέψει να σπάσει.
blog comments powered by Disqus