ΡΣΤ ροπή στροφή τροπή
Λίγα λόγια για τα σύμβολα της ροπής στην ελληνική και διεθνή βιβλιογραφία:
Torque \(\quad \vec τ \quad\) is a measure of the force that can cause an object to rotate about an axis. Just as force is what causes an object to accelerate in linear kinematics, torque is what causes an object to acquire angular acceleration. Torque is a vector quantity. link
The Moment of a force \(\quad \vec M \quad\) is a measure of its tendency to cause a body to rotate about a specific point or axis. This is different from the tendency for a body to move, or translate, in the direction of the force. In order for a moment to develop, the force must act upon the body in such a manner that the body would begin to twist. This occurs every time a force is applied so that it does not pass through the centroid of the body. A moment is due to a force not having an equal and opposite force directly along it’s line of action. link
Ιδέες για γνωριμία με την έννοια της ροπής:

Με το γαλλικό κλειδί γιατί είναι ευκολότερη η στροφή μιας βίδας;

Γιατί ο λιγνός σηκώνει τον χοντρό στην τραμπάλα;
Γιατί μεταφέρουμε το σώμα μας πίσω για να νικήσουμε στην τραμπάλα;

Γιατί οι πόρτες στο εργαστήριο φυσικών επιστημών έχουν μπάρες πανικού;
Όπως και οι πόρτες στα νοσοκομεία απαιτούν μεγαλύτερη ροπή για να ανοιγοκλείσουν;
Ορισμός της ροπής στο σχολικό βιβλίο
Ροπή της δύναμης \(\quad F \quad\), ως προς τον άξονα περιστροφής ονομάζεται το διανυσματικό μέγεθος που έχει μέτρο ίσο με το γινόμενο του μέτρου της δύναμης επί την κάθετη απόσταση \(\quad l \quad\) της δύναμης από τον άξονα περιστροφής (μοχλοβραχίονας).
\[τ = F \cdot l\]Η ροπή έχει τη διεύθυνση του άξονα περιστροφής και η φορά της δίνεται από τον κανόνα του δεξιού χεριού. Μονάδα ροπής είναι το \(1 Ν m\).
Μοχλοβραχίονας σύνθετη λέξη που αποτελείται από την λέξη “μοχλός” και την λέξη “βραχίονας”
Ο σπουδαίος αρχαίος Έλληνας Φυσικός, Μαθηµατικός και Μηχανικός Αρχιµήδης ο Συρακούσιος (287-212 π.Χ.): Δῶς μοι πᾶ στῶ καὶ τὰν γᾶν κινάσω
Δως μου μέρος/(πού) να σταθώ (μοχλοβραχίονα) κι ως και τη γη μπορώ να κινήσω /(και τότε θα μπορούσα ακόμη και την Γη να κινήσω)
Βραχίονας: το ανώτερο τμήμα του χεριού, από τον ώμο μέχρι τον αγκώνα.
Ροπή δύναμης \(F\) ως προς σημείο \(Ο\) ονομάζουμε το διανυσματικό μέγεθος που έχει μέτρο ίσο με το γινόμενο του μέτρου της δύναμης επί την απόσταση της από το σημείο \(Ο\)
\[τ = F \cdot l\]διεύθυνση κάθετη στο επίπεδο που ορίζεται από τη δύναμη και το σημείο \(Ο\) και φορά που δίνεται από τον κανόνα του δεξιού χεριού.
Η πραγματικότητα;
Η ροπή μιας δύναμης F ως προς σημείο Ο ορίζεται από τη διανυσματικη σχέση
\[\vecτ = \vec r × \vec F\]όπου \(\vec r\) είναι ένα διάνυσμα με αρχή το σημείο \(Ο\) και τέλος ένα σημείο του διανύσματος \(\vec F\). Σύμφωνα με τον ορισμό του εξωτερικού γινομένου η ροπή είναι κάθετη στο επίπεδο που ορίζεται από τα διανύσματα \(\vec r\) και \(\vec F\) και η φορά της δίνεται από τον κανόνα του δεξιού χεριού.
Το μέτρο της ροπής που προκύπτει από τον ορισμό αυτό είναι
\[τ = r \cdot F \cdot ημφ\]όπου \(φ\) είναι η γωνία που σχηματίζει το διάνυσμα \(\vec r\) με το διάνυσμα \(\vec F\).
Μέθοδοι Υπολογισµού της Ροπής ∆ύναµης ως προς Σηµείο \(Ο\)
1η Μέθοδος
Σχεδιάζουµε τα διανύσµατα \(\vec r\) και \(\vec F\) µε κοινή αρχή και προσδιορίζουµε τη γωνία \(θ\) ανάµεσα στις διευθύνσεις τους. Υπάρχουν δύο γωνίες - διαλέγουµε τη µικρότερη \(0 ≤ θ ≤ 180^o\)
Υπολογίζουµε το µέτρο της ροπής από τη σχέση
\[τ = F \cdot r \cdot ηµθ\]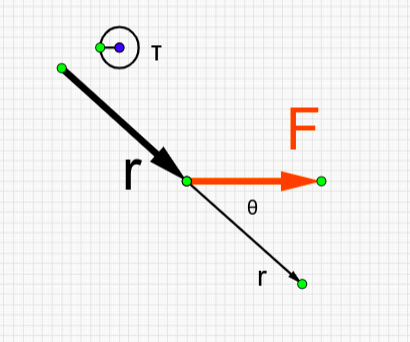
H διεύθυνση της ροπής είναι κάθετη στο επίπεδο των \(\vec r\) και \(\vec F\). Εάν η δύναµη \(F\) στρέφει το σηµείο εφαρµογής της αριστερόστροφα ως προς το \(Ο\) η αντίθετα από τη φορά των δεικτών του ρολογιού, η ροπή έχει θετική αλγεβρική τιµή (\(τ > 0\)). Στην αντίθετη περίπτωση, έχει αρνητική αλγεβρική τιµή.
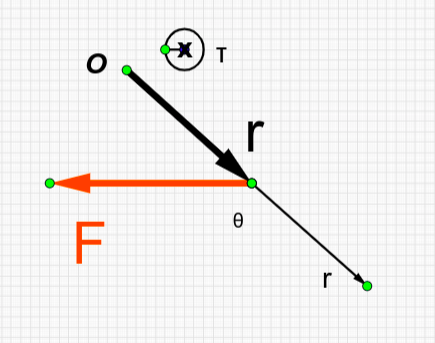
2η Μέθοδος
Προσδιορίζουµε την απόσταση \(d\) του σηµείου \(Ο\) από τον φορέα της δύναµης. H απόσταση \(d\) ονοµάζεται µοχλοβραχίονας της δύναµης. Υπολογίζουµε το µέτρο της ροπής από τη σχέση
\[τ = F \cdot d \Rightarrow τ = F \cdot r \cdot ημθ\]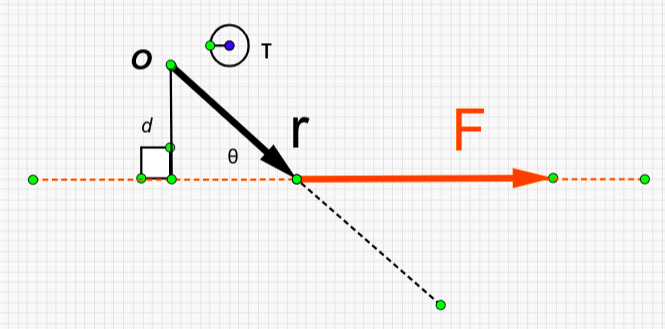
Προσδιορίζουµε το πρόσηµο της αλγεβρικής τιµής της ροπής όπως στην 1η µέθοδο.
3η Μέθοδος
Προσδιορίζουµε τo µέτρο \(F_x\) της κάθετης συνιστώσας της δύναµης στο διάνυσµα \(r\) Υπολογίζουµε το µέτρο της ροπής από τη σχέση
\[τ = F_x \cdot r \Rightarrow τ = F \cdot r \cdot ημθ\]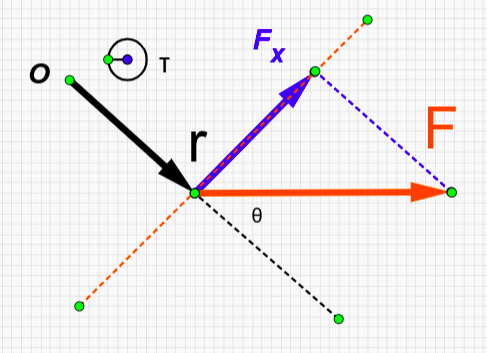
Προσδιορίζουµε το πρόσηµο της αλγεβρικής τιµής της ροπής όπως στην 1η µέθοδο.
Θεώρηµα των Ροπών
Η ροπή της συνισταµένης δύο (ή περισσότερων) δυνάµεων µε κοινό σηµείο εφαρµογής ισούται µε το άθροισµα των ροπών των δυνάµεων
\[\vec τ_{F_{ολ}} = \vec τ_{F_1} + \vec τ_{F_2}\]Το θεώρηµα ισχύει και στη γενικότερη περίπτωση που οι δυνάµεις δεν έχουν κοινό σηµείο εφαρµογής, αλλά οι φορείς τους τέµνονται στο ίδιο σηµείο. Σε αυτή την περίπτωση οι δυνάµεις ονοµάζονται συντρέχουσες. ∆υνάµεις µε κοινό σηµείο εφαρµογής αποτελούν ειδική περίπτωση συντρεχουσών δυνάµεων.
Το θεώρηµα ισχύει για παράλληλες δυνάµεις όταν έχουν τον ίδιο φορέα (είναι συγγραµµικές). ∆εν ισχύει γενικά για παράλληλες δυνάµεις µε διαφορετικούς φορείς (ζεύγος δυνάµεων).
Απόδειξη
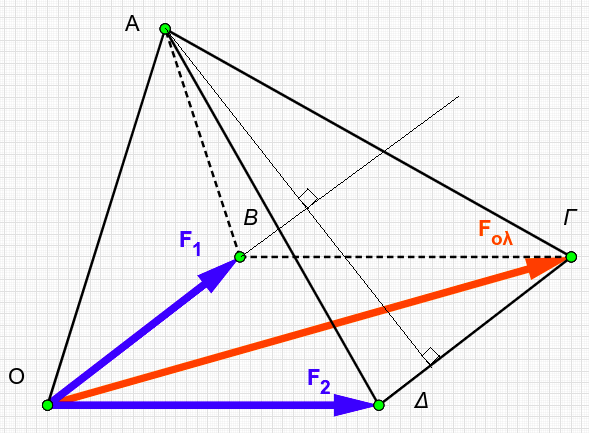
Θεωρούμε τις ροπές των δυνάμεων \(τ_{F_1}\) και \(τ_{F_2}\) ως προς το σημείο \(Α\) καθώς και τη ροπή της συνισταμένης \(τ_{F_{ολ}}\) ως προς το ίδιο αυτό σημείο. Η ως προς \(Α\) ροπή \(τ_{F_1}\) έχει μέτρο ίσο με το διπλάσιο του εμβαδού του τριγώνου \(ΟΑΒ\).
\[(ΟΑΒ) = \frac{β \cdot υ}{2} \Rightarrow (OAB) = \frac{F_1 \cdot d_1}{2} \Rightarrow τ_{F_1} = 2 \cdot (OAB)\]Η ως προς \(Α\) ροπή \(τ_{F_2}\) έχει μέτρο ίσο με το διπλάσιο του εμβαδού του τριγώνου \(ΟΑΔ\).
\[(ΟΑΔ) = \frac{β \cdot υ}{2} \Rightarrow (OAΔ) = \frac{F_2 \cdot d_2}{2} \Rightarrow τ_{F_2} = 2 \cdot (OAΔ)\]Η ως προς Α ροπή της συνισταμένης \(τ_{F_{ολ}}\) έχει μέτρο ίσο με το διπλάσιο του εμβαδού του τριγώνου \(ΟΑΓ\).
\[(ΟΑΓ) = \frac{β \cdot υ}{2} \Rightarrow (OAΓ) = \frac{F_{ολ} \cdot d_{ολ}}{2} \Rightarrow τ_{F_{ολ}} = 2 \cdot (OAΓ)\]Αν είναι \(Ε\) το εμβαδόν του παραλληλογράμμου \(ΟΒΓΔ\)
\[(ΟΑΓΔ) = (ΟΑΔ) + (ΔΑΓ) \Rightarrow (ΟΑΓΔ) = \frac{1}{2} τ_{F_2} + (ΔΑΓ)\] \[(ΟΑΓΔ) = (ΟΑΓ) + (ΟΓΔ) \Rightarrow (OAΓΔ) = \frac{1}{2} τ_{F_{ολ}} + \frac{1}{2} Ε\] \[(ΔΑΓ) = \frac{1}{2} τ_{F_1} + \frac{1}{2} Ε\]Από τις παραπάνω σχέσεις προκύπτει ότι
\[τ_{F_1} + τ_{F_2} = τ_{F_{ολ}}\]Ζεύγος δυνάμεων
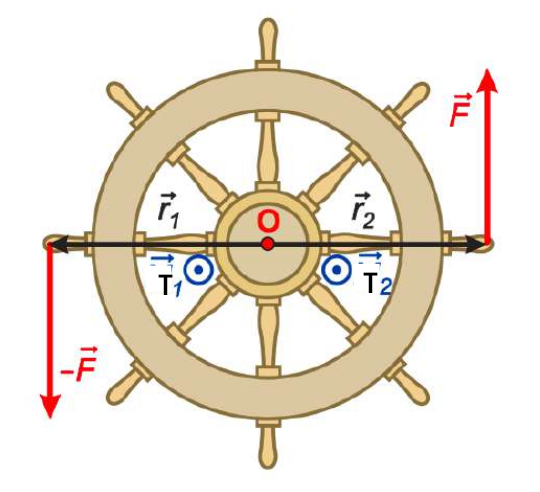
H παραπάνω εικόνα απεικονίζει το τιµόνι ενός πλοίου. Ο άξονας περιστροφής του τιµονιού είναι κάθετος στο επίπεδο της σελίδας, και διέρχεται από το κέντρο του τιµονιού. Σε δύο αντιδιαµετρικά σηµεία του τιµονιού εφαρµόζονται οι αντίθετες δυνάµεις \(\vec F\) και \(- \vec F\)
Το σύστηµα δύο αντίθετων δυνάµεων, που εφαρµόζονται σε διαφορετικά σηµεία ενός σώµατος, ονοµάζεται ζεύγος δυνάµεων.
Η συνισταµένη των δυνάµεων \(\vec F\) και \(- \vec F\) είναι ίση µε µηδέν:
\[Σ \vec F = \vec F - \vec F = 0\]Άρα, το ζεύγος δυνάµεων δεν µεταβάλλει τη µεταφορική ταχύτητα του τιµονιού. Κάθε µία από τις δυνάµεις εξασκεί ροπή, η οποία τείνει να περιστρέψει αριστερόστροφα το τιµόνι ή αντίθετα από την φορά των δεικτών του ρολογιού. Οι αλγεβρικές τιµές των ροπών των δύο δυνάµεων ως προς το \(Ο\) είναι θετικές και ίσες µεταξύ τους:
\[τ_1 = τ_2 = F \cdot R\]όπου \(R = r_1 = r_2\) είναι η απόσταση του σηµείου εφαρµογής κάθε δύναµης από τον άξονα περιστροφής. Tα διανύσµατα \(\vec τ_1\) και \(\vec τ_2\) είναι οµόρροπα (κάθετα στο επίπεδο των δύο φορέων, µε φορά προς τον αναγνώστη). Η συνολική ροπή έχει την ίδια κατεύθυνση, και αλγεβρική τιµή
\[τ_{ολ} = τ_1 + τ_2 \Rightarrow τ_{ολ} = F \cdot 2 \cdot R \Rightarrow τ_{ολ} = F \cdot d\]Το µέγεθος \(d = 2R\) ισούται µε την απόσταση µεταξύ των φορέων των δύο δυνάµεων.
Υπολογίσαµε τη ροπή του ζεύγους ως προς το σηµείο \(Ο\). Αποδεικνύεται όµως ότι η ροπή ενός ζεύγους δυνάµεων είναι σταθερή ως προς οποιοδήποτε σηµείο του χώρου.
Άρα ένα ζεύγος δυνάµεων δεν προκαλεί µεταφορική κίνηση αλλά µπορεί να προκαλέσει περιστροφή ενός σώµατος. Το µέτρο της συνολικής ροπής του ζεύγους δυνάµεων ισούται µε το γινόμενο του μέτρου \(F\) κάθε δύναµης, επί τη συνολική απόσταση \(d\) µεταξύ των φορέων των δυνάμεων. Η διεύθυνση της ροπής ζεύγους είναι κάθετη στο επίπεδο, που ορίζουν οι παράλληλοι φορείς των δυνάµεων. H φορά της ροπής ζεύγους καθορίζεται από τον κανόνα της δεξιάς παλάµης: Λυγίζουµε τα δάκτυλα προς την κατεύθυνση περιστροφής, και ο τεντωµένος αντίχειρας δείχνει την κατεύθυνση της ροπής. Σε αντίθεση με την ροπή της δύναμης ως προς σημείο ή ως προς άξονα περιστροφής, η ροπή του ζεύγους δεν απαιτεί σημείο ή άξονα αναφοράς.
1ος Νόμος του Νεύτωνα
Ήρθε η ώρα να τροποποιήσουμε τον πρώτο νόμο του Νεύτωνα, διατυπώνοντάς τον γενικά για το στερεό σώμα.
Ένα στερεό σώμα διατηρεί την κινητική του κατάσταση την μεταφορική ή την περιστροφική όταν σε αυτό δεν ασκούνται δυνάμεις (αν ασκούνται η συνισταμένη τους πρέπει να είναι μηδέν) και ροπές ως προς οποιοδήποτε σημείο (εξαιρείται η περίπωση της ροπής ζεύγους δυνάμεων).
Θα λέμε ότι ένα στερεό σώμα ισσορροπεί ακίνητο ή δεν περιστρέφεται όταν η ταχύτητα του κέντρου μάζας του ή η γωνιακή ταχύτητα ως προς οποιοδήποτε σημείο του είναι μηδέν.
θα λέμε ότι ένα στερεό σώμα ισσορροπεί κινούμενο ή περιστρεφόμενο όταν έχει σταθερή ταχύτητα το κέντρο μάζας του ή περιστρέφετται με σταθερή γωνιακή ταχύτητα ως προς οποιοδήποτε σημείο του.
Σε κάθε περίπτωση θα πρέπει να ισχύει:
\[Σ \vec F = 0 \quad Σ \vec τ = 0\]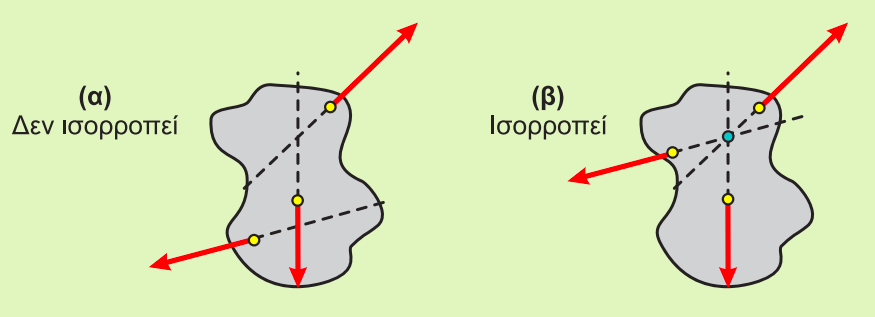
Για το τέλος της παρουσίασης θα αναφερθεί μια πολύ χρήσιμη ιδιότητα.
Για να ισσορροπεί ένα στερεό σώμα στο οποίο ασκούνται τρεις ομοεπίππεδες μη παράλληλες δυνάμεις, οι φορείς των δυνάμεων πρέπει να διέρχονται από το ίδιο σημείο. Εάν δεν ισχύει αυτό το άθροισµα των τριών ροπών δεν μηδενίζεται.
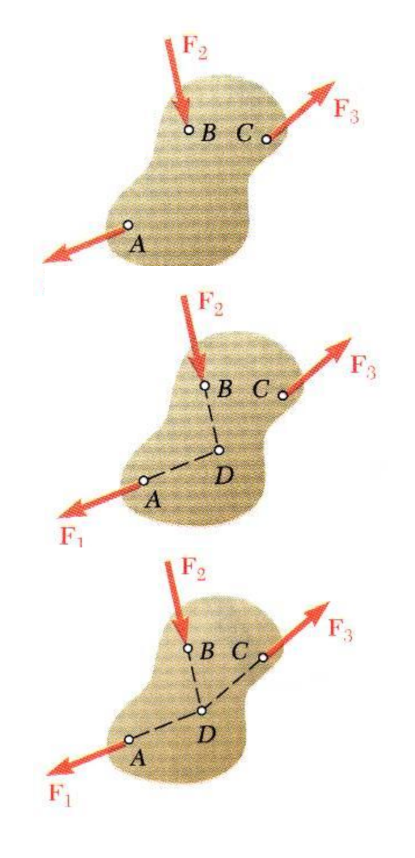
Στο προηγούμενο σχήμα απεικονίζεται ένα στερεό σώμα στο οποίο ασκούνται τρεις ομοεπίππεδες μη παράλληλες δυνάμεις. Για να ισσορροπεί το στερεό θα πρέπει να ισχύουν:
\[Σ \vec F = \vec F_1 + \vec F_2 + \vec F_3 = 0\]Επίσης θα πρέπει το άθροισμα των ροπών των δυνάμεων να μηδενίζεται για οποιοδήποτε σημείο.
\[Σ \vec τ = \vec τ_1 + \vec τ_2 + \vec τ_3 = 0\]Έστω ότι οι φορείς των δυνάμεων \(F_1\) και \(F_2\) τέμνονται στο σημείο \(D\). Αν υποθέσουμε ότι ο φορέας της \(F_3\) δεν διέρχεται από το σημείο \(D\) τότε οι ροπές των δυνάμεων \(F_1\) και \(F_2\) μηδενίζονται ως προς το σημείο \(D\) αλλά η ροπή της δύναμης \(F_3\) θα είναι μη μηδενική ως προς αυτό το σημείο. Άρα δεν ικανοποιείται η συνθήκη για τον μηδενισμο των ροπών. Για να ικανοποιείται και αυτή η συνθήκη θα πρέπει ο φορέας της δύναμης \(F_3\) να διέρχεται από το σημείο \(D\).
blog comments powered by Disqus