Ρευστά και ταλάντωση

Η Νικολέτα, η Δάφνη και η Λαμπρινή είναι μαθήτριες της Γ΄ λυκείου που λατρεύουν τη φυσική. Έτσι με την παρότρυνση του καθηγητή τους αποφάσισαν να δημιουργήσουν τη δική τους άσκηση και το σχήμα φαίνεται παρακάτω:

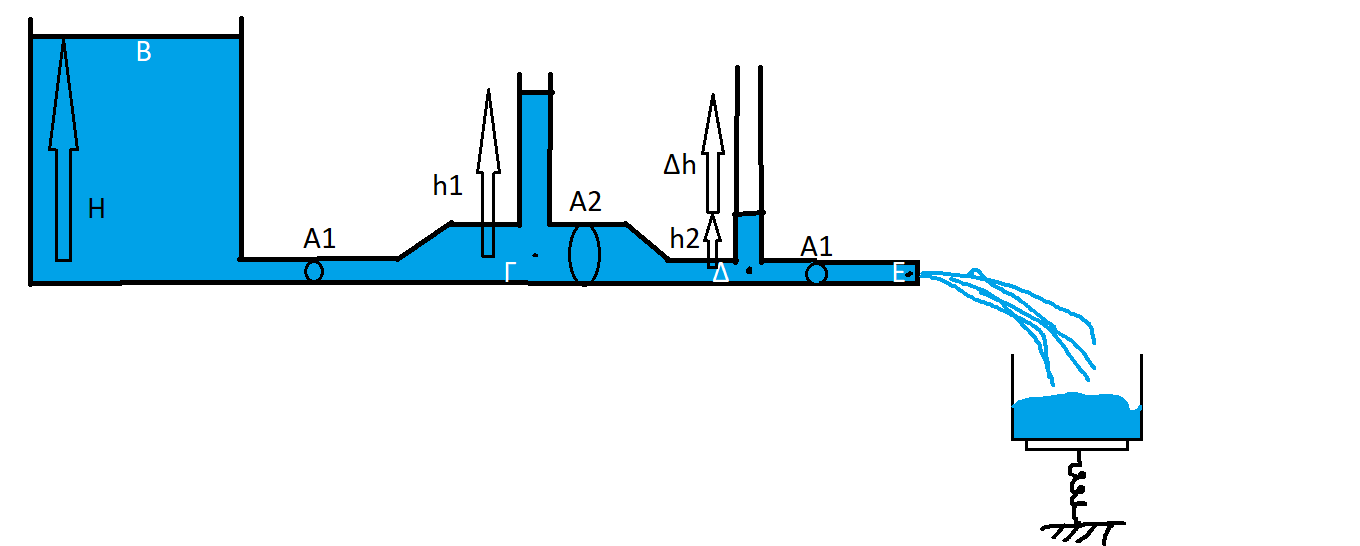
Σε μία ανοιχτή δεξαμενή μεγάλου όγκου περιέχεται νερό, η ελεύθερη επιφάνεια του οποίου βρίσκεται σε ύψους \(Η = 20cm\) . Τη στιγμή \(t_o=0s\) ανοίγουμε την οπή \(Ε\) και νερό ρέει μέσω του οριζόντιου σωλήνα μεταβλητής διατομής με \(Α_1 = 5cm^2\) και \(Α_2 = 10cm^2\), εξέρχεται από το σημείο \(\) και αφού εκτελέσει οριζόντια βολή καταλήγει όλο σε αβαρές δοχείο όγκου \(V = 1m^3\) χωρίς να χύνεται καθόλου έξω. Το δοχείο βρίσκεται πάνω σε δίσκο ο οποίος είναι στερεωμένος πάνω σε ιδανικό ελατήριο σταθεράς \(k = 1000 \frac{Ν}{m}\). Καθώς το δοχείο γεμίζει, το ελατήριο συσπειρώνεται και τη στιγμή που το δοχείο έχει γεμίσει πλήρως, το ελατήριο έχει υποστεί την μέγιστη συσπείρωση. Tη στιγμή αυτή κλείνουμε την οπή \(Ε\) και ταυτόχρονα αφαιρούμε το δοχείο και ο δίσκος μάζας \(m=1000kg\) αρχίζει να ταλαντώνεται. Για την ταλάντωση να θεωρήσετε θετική φορά την προς τα κάτω και να Θεωρήστε το δοχείο με το νερό ως υλικό σημείο, δηλαδή για την ταλάντωση του δίσκου μην λάβετε υπ’ όψη σας την ατμοσφαιρική πίεση.

Δίνονται η πυκνότητα του νερού \(ρ = 1 \frac{gr}{cm^3}\), η επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\), το ύψος της στήλης του νερού στον πρώτο κατακόρυφο σωλήνα \(h_1 = 15cm\) και η ατμοσφαιρική πίεση \(p_{atm} = 10^5 Pa\). Θεωρήστε το νερό ως ασυμπίεστο ιδανικό ρευστό και την ροή του στρωτή.

Ζητούμενα

1. Να υπολογίσετε την διαφορά ύψους μεταξύ των δύο κατακόρυφων σωλήνων \(Δh\).
2. Να υπολογίσετε το χρονικό διάστημα \(Δt\) στο οποίο θα γεμίσει το δοχείο.
3. Να γράψετε την εξίσωση ταλάντωσης του δίσκου.
4. Να κατασκευάσετε τα διαγράμματα στιγμιαίας απομάκρυνσης, ταχύτητας και επιτάχυνσης του δίσκου κατά την διάρκεια μίας περιόδου.