Η διατήρηση της ενέργειας και η εξίσωση του Bernoulli
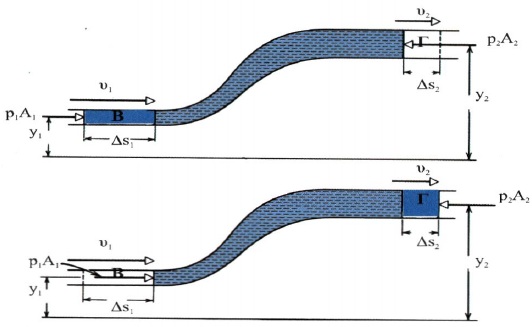
Έστω ότι έχουμε ένα σωλήνα μεταβλητής διατομής μέσα στον οποίο ρέει ένα ασυμπίεστο ρευστό όπως φαίνεται στο παραπάνω σχήμα. Θα εξετάσουμε την πίεση σε δύο σημεία \(Β\) και \(Γ\) του σωλήνα. Το σημείο \(Β\) βρίσκεται σε ύψος \(y_1\) από το έδαφος και ο σωλήνας έχει στην περιοχή του \(Β\) διατομή \(Α_1\). Η πίεση του ρευστού στο \(Β\) είναι \(p_1\). Το σημείο \(Γ\) βρίσκεται σε ύψος \(y_2\) από το έδαφος, η διατομή του σωλήνα εκεί είναι \(Α_2\) και η πίεση \(p_2\). Αν θεωρήσουμε σαν σύστημα το ρευστό από το \(Β\) μέχρι το \(Γ\), βλέπουμε ότι δέχεται από το υπόλοιπο ρευστό μια δύναμη \(p_1 \cdot Α_1\) στην περιοχή του \(Β\) και μια δύναμη, την \(p_2 \cdot A_2\) στην περιοχή του \(Γ\), με φορά αντίθετη με τη φορά της \(p_1 \cdot A_1\). Σ’ ένα πολύ μικρό χρονικό διάστημα \(Δt\) ένα στοιχειώδες τμήμα του ρευστού στην περιοχή του \(Β\) μετατοπίζεται κατά \(Δx_1\) ενώ ένα αντίστοιχο τμήμα του ρευστού ίσης μάζας, άρα και όγκου, στην περιοχή του \(Γ\) μετατοπίζεται κατά \(Δx_2\).
Συγκεντρώνουμε την προσοχή μας στο περιβάλλον ρευστό που υπάρχει στην περιοχή του \(Β\). Τα μόρια του ρευστού που αποτελούν το αριστερά περιβάλλον ρευστό ασκούν δύναμη \(p_1 \cdot A_1\) στο ρευστό που θεωρούμε ως σύστημα. Αυτή η δύναμη μετατοπίζει το σημείο εφαρμογής της κατά την διεύθυνσή της άρα το έργο της είναι ένα παραγόμενο έργο, δηλαδή είναι θετικό.
\[ΔW_1 = + p_1 \cdot A_1 \cdot Δx_1 \Rightarrow ΔW_1 = p_1 \cdot ΔV\]Αυτή η μεταβολή μας θυμίζει την ισοβαρή εκτόνωση για το αριστερά περιβάλλον ρευστό, που έχουμε μάθει στην Β’ Λυκείου για την οποία γνωρίζουμε ότι \(ΔV>0 \Rightarrow ΔW_1>0\)
Θετικό έργο σημαίνει ότι ενέργεια φεύγει από το αριστερά περιβάλλον ρευστό και μεταφέρεται στο ρευστό που θεωρούμε ως σύστημα. Αυτή την ενέργεια ανά μονάδα όγκου που ρέει από τα αριστερά προς το ρευστό που θεωρούμε σύστημα την ονομάζουμε πίεση \(p_1\). Δηλαδή η πίεση που ασκεί το αριστερά περιβάλλον ρευστό στο ρευστό που θεωρούμε ως σύστημα μπορούμε να την σκεφτόμαστε και σαν δύναμη ανά μονάδα επιφάνειας αλλά και σαν πυκνότητα ροής ενέργειας, δηλαδή σαν ενέργεια ανά μονάδα όγκου και εκφράζει το “σπρώχνω” του αριστερά ρευστού προς το σύστημα ρευστό.
Συγκεντρώνουμε τώρα την προσοχή μας στο περιβάλλον ρευστό που υπάρχει στην περιοχή του \(Γ\). Τα μόρια του ρευστού που αποτελούν το δεξιά περιβάλλον ρευστό ασκούν δύναμη \(p_2 \cdot A_2\) στο ρευστό που θεωρούμε ως σύστημα. Αυτή η δύναμη μετατοπίζει το σημείο εφαρμογής της αντίθετα από την διεύθυνσή της άρα το έργο της είναι ένα καταναλισκόμενο έργο, δηλαδή είναι αρνητικό.
\[ΔW_2 = - p_2 \cdot A_2 \cdot Δx_2 \Rightarrow ΔW_2 = - p_2 \cdot ΔV\]Αυτή η μεταβολή μας θυμίζει την ισοβαρή συμπίεση για το δεξιά περιβάλλον ρευστό που έχουμε μάθει στην Β’ Λυκείου για την οποία γνωρίζουμε ότι \(ΔV<0 \Rightarrow ΔW_2<0\)
Αρνητικό έργο σημαίνει ότι ενέργεια έρχεται από το ρευστό που θεωρούμε ως σύστημα προς το δεξιά περιβάλλον ρευστό. Αυτή την ενέργεια ανά μονάδα όγκου που ρέει από το ρευστό που θεωρούμε σύστημα προς το δεξιά περιβάλλον ρευστό την ονομάζουμε πίεση \(p_2\). Δηλαδή η πίεση που ασκεί το ρευστό που θεωρούμε ως σύστημα προς το δεξιά περιβάλλον ρευστό μπορούμε να την σκεφτόμαστε και σαν δύναμη ανά μονάδα επιφάνειας αλλά και σαν πυκνότητα ροής ενέργειας, δηλαδή σαν ενέργεια ανά μονάδα όγκου και εκφράζει το “σπρώχνω” του ρευστού που θεωρούμε ως σύστημα προς το δεξιά περιβάλλον ρευστό.
Άρα για το σύστημά μας θετικό έργο σημαίνει την ενέργεια ανά μονάδα όγκου που έρχεται από αριστερά και αρνητικό έργο σημαίνει την ενέργεια ανά μονάδα όγκου που φεύγει προς τα δεξιά.
Αν θέλουμε να υπολογίσουμε το συνολικό έργο θα έχουμε:
\[ΔW = ΔW_1 + ΔW_2 \Rightarrow ΔW = (p_1 - p_2) \cdot ΔV\]Για να μπορέσουμε τώρα να εφαρμόσουμε το θεώρημα έργου ενέργειας σε μικρό χρονικό διάστημα \(Δt\) θα χρειαστούμε ένα πριν και ένα μετά. Συνήθως μέχρι σήμερα εφαρμόζουμε αυτό το θεώρημα από μια θέση σε μια άλλη. Ξεχνάμε λοιπόν το αριστερά περιβάλλον ρευστό και στην θέση του έχουμε ένα πριν ή την αρχική θέση και παρόμοια ξεχνάμε το δεξιά περιβάλλον ρευστό και στην θέση του έχουμε ένα μετά ή την τελική θέση.
\[ΔΚ = ΣW \Rightarrow ΔΚ = W_B + ΔW \Rightarrow ΔΚ - W_B = ΔW\]Για την μεταβολή της βαρυτικής δυναμικής ενέργειας γνωρίζουμε ότι \(ΔU = - W_B\) και με βάση τη σχέση που αποδείξαμε για το συνολικό έργο του περιβάλλοντος ρευστού \(ΔW\) έχουμε:
\[ΔΚ + ΔU = (p_1 - p_2) \cdot ΔV \Rightarrow \frac{ΔΚ}{ΔV} + \frac{ΔU}{ΔV} = p_1 - p_2\] \[\frac{ΔΚ}{ΔV} + \frac{ΔU}{ΔV} + p_2 - p_1 = 0 \Rightarrow \frac{ΔΚ}{ΔV} + \frac{ΔU}{ΔV} + ΔP = 0\]Βρήκαμε ότι υπάρχει κάποια ποσότητα που η μεταβολή της είναι μηδέν. Αυτό σημαίνει ότι η ποσότητα αυτή παραμένει σταθερή. Αυτή την ποσότητα μπορούμε να την ονομάζουμε ολική πίεση και είναι το άθροισμα τριών ειδών πίεσης.
\[Δ(\frac{K}{ΔV} + \frac{U}{ΔV} + p ) = 0 \Rightarrow \frac{K}{ΔV} + \frac{U}{ΔV} + p = σταθ.\] \[\frac{K}{ΔV} = \frac{\frac{1}{2} \cdot Δm \cdot υ^2}{ΔV} = \frac{\frac{1}{2} \cdot ρ \cdot ΔV \cdot υ^2}{ΔV} = \frac{1}{2} \cdot ρ \cdot υ^2\]Την ποσότητα \(\frac{K}{ΔV} = \frac{1}{2} \cdot ρ \cdot υ^2\) την ονομάζουμε δυναμική πίεση και είναι η κινητική ενέργεια ανά μονάδα όγκου ή πυκνότητα ροής κινητικής ενέργειας.
\[\frac{U}{ΔV} = \frac{Δm \cdot g \cdot h}{ΔV} = \frac{ρ \cdot ΔV \cdot g \cdot h}{ΔV} = ρ \cdot g \cdot h\]Την ποσότητα \(\frac{U}{ΔV} = ρ \cdot g \cdot h\) την ονομάζουμε υψομετρική πίεση και είναι η δυναμική ενέργεια ανά μονάδα όγκου ή πυκνότητα ροής δυναμικής ενέργειας.
Την ποσότητα \(p\) την ονομάζουμε στατική πίεση και είναι το έργο του περιβάλλοντος ρευστού ανά μονάδα όγκου ή πυκνότητα ροής έργου.
Τέλος να πούμε και λίγα λόγια για τα πρόσημα αυτών των μεγεθών.
Ποια η φυσική σημασία της σχέσης \(\frac{ΔΚ}{ΔV}>0\)
Η μεταβολή της δυναμικής πίεσης είναι θετική ή με απλά λόγια η κινητική ενέργεια ανά μονάδα όγκου είναι θετική. Όταν το ρευστό (αυτό που θεωρούμε σύστημα) μεταφέρεται από αγωγό του οποίου η διατομή ελαττώνεται, τότε όπως γνωρίζουμε από την εξίσωση της συνέχειας αφού η διατομή ελαττώνεται η ταχύτητα των μορίων του ρευστού αυξάνεται και αυτό έχει σαν συνέπεια να αυξάνεται η πυκνότητα ροής κινητικής ενέργειας, δηλαδή η κινητική ενέργεια ανά μονάδα όγκου.
Ποια η φυσική σημασία της σχέσης \(\frac{ΔΚ}{ΔV}<0\)
Η μεταβολή της δυναμικής πίεση είναι αρνητική ή με απλά λόγια η κινητική ενέργεια ανά μονάδα όγκου είναι αρνητική. Όταν το ρευστό (αυτό που θεωρούμε σύστημα) μεταφέρεται από αγωγό του οποίου η διατομή αυξάνεται, τότε όπως γνωρίζουμε από την εξίσωση της συνέχειας αφού η διατομή αυξάνεται η ταχύτητα των μορίων του ρευστού ελαττώνεται και αυτό έχει σαν συνέπεια να ελαττώνεται η πυκνότητα ροής κινητικής ενέργειας, δηλαδή η κινητική ενέργεια ανά μονάδα όγκου.
Ποια η φυσική σημασία της σχέσης \(\frac{ΔU}{ΔV}>0\)
Η μεταβολή της υψομετρικής πίεσης είναι θετική ή με απλά λόγια η δυναμική ενέργεια ανά μονάδα όγκου είναι θετική. Όταν το ρευστό (αυτό που θεωρούμε σύστημα) ανέρχεται σε κάποιον αγωγό, τότε η τελική βαρυτική δυναμική ενέργεια είναι μεγαλύτερη από την αρχική και αυτό σημαίνει ότι αυξάνεται το υψόμετρο \(h\) και αυτό έχει σαν συνέπεια να αυξάνεται η πυκνότητα ροής δυναμικής ενέργειας δηλαδή η δυναμική ενέργεια ανά μονάδα όγκου.
Ποια η φυσική σημασία της σχέσης \(\frac{ΔU}{ΔV}<0\)
Η μεταβολή της υψομετρικής πίεσης είναι αρνητική ή με απλά λόγια η δυναμική ενέργεια ανά μονάδα όγκου είναι αρνητική. Όταν το ρευστό (αυτό που θεωρούμε σύστημα) κατέρχεται σε κάποιον αγωγό, τότε η τελική βαρυτική δυναμική ενέργεια είναι μικρότερη από την αρχική και αυτό σημαίνει ότι ελαττώνεται το υψόμετρο \(h\) και αυτό έχει σαν συνέπεια να ελαττώνεται η πυκνότητα ροής δυναμικής ενέργειας δηλαδή η δυναμική ενέργεια ανά μονάδα όγκου.
Ποια η φυσική σημασία της σχέσης \(Δp>0\)
Η μεταβολή της στατικής πίεσης είναι θετική ή με απλά λόγια το έργο του περιβάλλοντος ρευστού ανά μονάδα όγκου είναι αρνητικό. Εδώ χρειάζεται προσοχή. Όταν η μεταβολή της στατικής πίεσης είναι θετική ισχύει
\[p_2 - p_1 > 0 \Rightarrow p_1 - p_2 < 0 \Rightarrow ΔW < 0\]Αφού \(ΔW = (p_1 - p_2) \cdot ΔV\)
Δηλαδή όταν η μεταβολή της στατικής πίεσης είναι θετική αυτό σημαίνει ότι το ρευστό που θεωρούμε ως σύστημα, έχει πάρει μικρότερη \(p_1\) ενέργεια ανά μονάδα όγκου από το αριστερά περιβάλλον ρευστό, ενώ έχει δώσει μεγαλύτερη \(p_2\) ενέργεια ανά μονάδα όγκου προς το δεξιά περιβάλλον ρευστό και τελικά έδωσε περισσότερη ενέργεια από αυτή που πήρε, αφού
\[ΔW = (p_1 - p_2) \cdot ΔV \Rightarrow ΔW < 0\]Ποια η φυσική σημασία της σχέσης \(Δp<0\)
Η μεταβολή της στατικής πίεσης είναι αρνητική ή με απλά λόγια το έργο του περιβάλλοντος ρευστού ανά μονάδα όγκου είναι θετικό. Πάλι εδώ χρειάζεται προσοχή. Όταν η μεταβολή της στατικής πίεσης είναι αρνητική ισχύει
\[p_2 - p_1 < 0 \Rightarrow p_1 - p_2 > 0 \Rightarrow ΔW > 0\]Αφού \(ΔW = (p_1 - p_2) \cdot ΔV\)
Δηλαδή όταν η μεταβολή της στατικής πίεσης είναι αρνητική αυτό σημαίνει ότι το ρευστό που θεωρούμε ως σύστημα, έχει πάρει μεγαλύτερη \(p_1\) ενέργεια ανά μονάδα όγκου από το αριστερά περιβάλλον ρευστό, ενώ έχει δώσει μικρότερη \(p_2\) ενέργεια ανά μονάδα όγκου προς το δεξιά περιβάλλον ρευστό και τελικά του έμεινε η διαφορά των δύο ενεργειών
\[ΔW = (p_1 - p_2) \cdot ΔV \Rightarrow ΔW > 0\]Καταλαβαίνουμε λοιπόν την στατική πίεση σαν την ενέργεια που μας προσφέρει το αριστερά περιβάλλον ρευστό την οποία το σύστημά μας την προσφέρει με την σειρά του στο δεξιά περιβάλλον ρευστό.
blog comments powered by Disqus