Προσομοίωση 2021 Κυριακή 14 Φεβρουαρίου
ΘΕΜΑ A
Στις ερωτήσεις \(Α_1-Α_4\) να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την
ημιτελή πρόταση.
\(A_1\)
Όταν μια μικρή σφαίρα μάζας \(m\) και ταχύτητας \(υ\) προσπέσει κάθετα σε κατακόρυφο τοίχο και συγκρουσθεί με αυτόν ελαστικά, τότε το μέτρο της μεταβολής της ορμής της είναι
- $$ 0 $$
- $$ 2 \cdot m \cdot υ $$
- $$ m \cdot υ $$
- $$ m \cdot \frac{Δυ}{Δt} $$
\(A_2\)
Η δυναμική ενέργεια ενός συστήματος που εκτελεί απλή αρμονική ταλάντωση
- είναι μέγιστη στη θέση ισορροπίας
- αυξάνεται όταν το σώμα επιταχύνεται
- είναι ανάλογη με την απομάκρυνση του σώματος από τη θέση ισορροπίας του
- μεγιστοποιείται δύο φορές σε κάθε πλήρη ταλάντωση
\(A_3\)
Σύμφωνα με τον κανόνα του \(Lenz\), το επαγωγικό ρεύμα
- έχει τέτοια φορά ώστε να δημιουργεί επαγωγική τάση
- έχει τέτοια φορά ώστε το μαγνητικό του πεδίο να αντιτίθεται στο αίτιο που το προκάλεσε
- έχει τέτοια φορά ώστε να δημιουργεί μαγνητική ροή
- έχει τη φορά της δύναμης Laplace
\(A_4\)
Μεταλλικό πλαίσιο (αμελητέας ωμικής αντίστασης) στρέφεται με σταθερή γωνιακή ταχύτητα \(ω\) μέσα σε ομογενές μαγνητικό πεδίο \(Β\). Στα άκρα του πλαισίου συνδέεται ωμικός αντιστάτης αντίστασης \(R\). H παραγόμενη από το πλαίσιο εναλλασσόμενη τάση δίνεται από την εξίσωση
\[υ = 200 \cdot \sqrt2 \cdot ημ(100πt) \quad (S.I.)\]Αν διπλασιάσουμε τη συχνότητα περιστροφής του πλαισίου, τότε η εξίσωση της εναλλασσόμενης τάσης δίνεται από την σχέση:
- $$ υ = 200 \sqrt2 \cdot ημ(200πt) $$
- $$ υ = 400 \sqrt2 \cdot ημ(100πt) $$
- $$ υ = 400 \sqrt2 \cdot ημ(200πt) $$
- $$ υ = 200 \cdot ημ(200πt) $$
\(A_5\)
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
α. Η δύναμη Laplace που ασκείται σε ευθύγραμμο ρευματοφόρο αγωγό όταν αυτός βρίσκεται σε ομογενές μαγνητικό πεδίο εξαρτάται από το βάρος του αγωγού
β. Η ένταση του μαγνητικού πεδίου στο κέντρο του σωληνοειδούς εξαρτάται από την ένταση του ρεύματος που διαρρέει το σωληνοειδές
γ. Στα αμορτισέρ ενός αυτοκινήτου επιδιώκουμε η σταθερά απόσβεσης να είναι όσο το δυνατόν μικρότερη
δ. Σε μια εξαναγκασμένη ταλάντωση, το σύστημα που ταλαντώνεται βρίσκεται σε κατάσταση συντονισμού. Αν διπλασιάσουμε τη συχνότητα του διεγέρτη και ταυτόχρονα διπλασιάσουμε τη μάζα του συστήματος, τότε συνεχίζουμε να βρισκόμαστε σε κατάσταση συντονισμού
ε. Διακροτήματα προκύπτουν από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων με ίδιο πλάτος που εξελίσσονται στην ίδια διεύθυνση, γύρω από την ίδια θέση ισορροπίας και έχουν παραπλήσιες συχνότητες
ΘΕΜΑ Β
\(Β_1\)
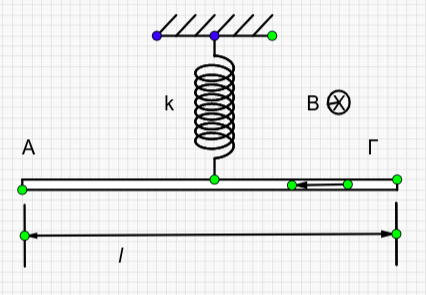
Ένας αγωγός \(ΑΓ\) μάζας \(m\) και μήκους \(l\) ισορροπεί σε κατακόρυφο επίπεδο με το κέντρο μάζας του να είναι στερεωμένο στο ελεύθερο άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς \(k\), το άλλο άκρο του οποίου είναι στερεωμένο σε σταθερό σημείο, όπως φαίνεται στο παραπάνω σχήμα. Κάθετα στο κατακόρυφο επίπεδο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης \(\vecΒ\) με κατεύθυνση αυτή που φαίνεται στο σχήμα. Την χρονική στιγμή \(t_o = 0\) τροφοδοτούμε τον αγωγό με ηλεκτρικό ρεύμα σταθερής έντασης \(Ι\) με φορά από το \(Γ\) προς το \(Α\). Αν δεν υπάρχουν τριβές το πλάτος \(Α\) της απλής αρμονικής ταλάντωσης που θα εκτελέσει ο αγωγός είναι:
- $$ Α = \frac{m \cdot g}{k} $$
- $$ Α = \frac{B \cdot I \cdot l}{k} $$
- $$ Α = \frac{B \cdot I \cdot l + m \cdot g}{k} $$
Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
\(Β_2\)
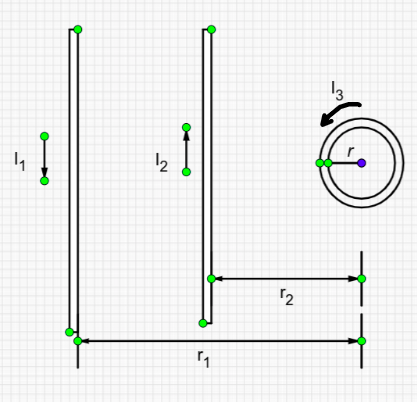
Οι δύο ευθύγραμμοι αγωγοί απείρου μήκους \((1)\) και \((2)\) του σχήματος είναι κατακόρυφοι, διαρρέονται από συνεχή ηλεκτρικά ρεύματα με σταθερές εντάσεις \(Ι_1\) και \(Ι_2 = 2 \cdot Ι_1\) και απέχουν αποστάσεις \(r_1 = 6 \cdot r\) και \(r_2 = 3 \cdot r\) αντίστοιχα από το κέντρο \(Κ\) κατακόρυφου κυκλικού αγωγού ακτίνας \(r\) που διαρρέεται από ηλεκτρικό ρεύμα έντασης \(Ι_3 = \frac{I_1}{π}\), με τις φορές των ρευμάτων αυτές που φαίνονται στο σχήμα. Το μέτρο της συνισταμένης έντασης του μαγνητικού πεδίου στο κέντρο Κ του κυκλικού αγωγού δίνεται από τη σχέση:
- $$ Β_k = k_μ \cdot \frac{11I_1}{3r} $$
- $$ Β_k = k_μ \cdot \frac{I_1}{3r} $$
- $$ Β_k = k_μ \cdot \frac{I_1}{r} $$
Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
\(Β_3\)
Βλήμα μάζας \(m\) κινείται οριζόντια με ταχύτητα \(υ\). Το βλήμα διαπερνά ακίνητο σώμα μάζας \(Μ = 9 \cdot m\) και εξέρχεται από αυτό με ταχύτητα \(\frac{υ}{5}\). Όμοιο βλήμα μάζας \(m\) που κινείται και αυτό οριζόντια με ταχύτητα \(υ\) σφηνώνεται σε ακίνητο σώμα μάζας \(Μ = 9 \cdot m\), οπότε σχηματίζεται συσσωμάτωμα. Αν \(Q_1\) και \(Q_2\) είναι οι θερμότητες που εκλύονται κατά τις κρούσεις της 1ης και της 2ης περίπτωσης αντίστοιχα ισχύει:
- $$ \frac{Q_1}{Q_2} = \frac{80}{81} $$
- $$ \frac{Q_1}{Q_2} = \frac{81}{80} $$
- $$ \frac{Q_1}{Q_2} = 1 $$
ΘΕΜΑ Γ
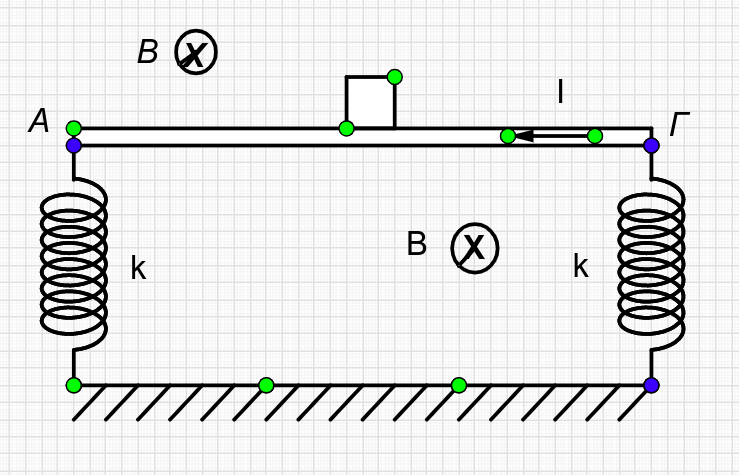
Μια ομογενής μεταλική ράβδος \(ΑΓ\) έχει μάζα \(Μ = 2.5 kg\) και μήκος \(l = 0.5m\) είναι στηριγμένη στα άκρα δύο κατακόρυφων ιδανικών ελατηρίων, ίδιου φυσικού μήκους και σταθεράς \(k = 100 \frac{N}{m}\). Στο μέσο της ράβδου τοποθετούμε ένα μικρό σώμα από μονωτικό υλικό με μάζα \(m = 0.5 kg\). Το σύστημα βρίσκεται σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης \(Β =2 Τ\). Η ράβδος διαρρέεται από συνεχές ρεύμα σταθερής έντασης \(Ι = 10Α\), με φορά από το \(Γ\) προς το \(Α\) και το σύστημα ισορροπεί ακίνητο.
\(Γ_1\) Να υπολογίσετε την συσπείρωση των ελατηρίων
Την χρονική στιγμή \(t_o = 0\) διακόπτουμε το ρεύμα που διαρρέει τη ράβδο. Αν θεωρήσουμε θετική φορά προς τα πάνω:
\(Γ_2\) Να δείξετε ότι το σύστημα της ράβδου και του μικρού σώματος, θα εκτελέσει απλή αρμονική ταλάντωση και να υπολογίσετε την ενέργεια της ταλάντωσης.
\(Γ_3\) Να υπολογίσετε την δύναμη που ασκεί η μεταλλική ράβδος στο μικρό σώμα σαν συνάρτηση της στιγμιαίας απομάκρυνσης της ράβδου από την θέση ισορροπίας της.
\(Γ_4\) Να υπολογίσετε την μέγιστη τιμή της έντασης του ρεύματος που πρέπει να διαρρέει την ράβδο, ώστε μετά την διακοπή του να μην χάνεται η επαφή των σωμάτων.
Δίνεται \(g = 10 \frac{m}{s^2}\).
ΘΕΜΑ Δ
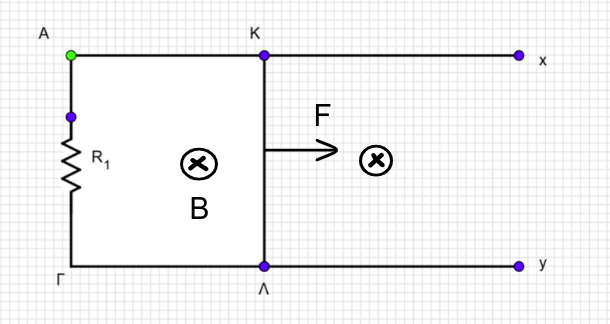
Ο ευθύγραμμος αγωγός \(ΚΛ\) του σχήματος έχει μάζα \(m = 0.1kg\), μήκος \(l = 1m\), αντίσταση \(R_2 = 2Ω\) και μπορεί να κινείται χωρίς τριβές, με τα άκρα του να εφάπτονται πάνω σε δύο παράλληλες οριζόντιες μεταλλικές ράβδους \(Αx\) και \(Γy\) μεγάλου μήκους και αμελητέας αντίστασης. Τα άκρα \(Α\) και \(Γ\) των δύο ράβδων είναι συνδεδεμένα με αντιστάτη, που έχει αντίσταση \(R_1 = 3Ω\). Η διάταξη βρίσκεται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο, έντασης \(Β = 1Τ\). Από κάποια χρονική στιγμή και μετά, ασκούμε στον αγωγό \(ΚΛ\) σταθερή οριζόντια δύναμη μέτρου \(F = 4N\), παράλληλη στις δύο ράβδους, οπότε αυτός αρχίζει να κινείται και αφού διανύσει διάστημα \(x_1 = 10m\), αποκτά οριακή ταχύτητα. Να υπολογίσετε:
\(Δ_1\) Την επαγωγική τάση που δημιουργείται στο κύκλωμα αφού ο αγωγός αποκτά την οριακή του ταχύτητα.
\(Δ_2\) Την ενέργεια που μετατρέπεται σε θερμότητα Joule στο κύκλωμα, από τη στιγμή που ο αγωγός \(ΚΛ\) άρχισε να κινείται, μέχρι τη στιγμή που απέκτησε την οριακή του ταχύτητα.
\(Δ_3\) Το ηλεκτρικό φορτίο που πέρασε από μια διατομή του κυκλώματος, από τη στιγμή που ο αγωγός \(ΚΛ\) άρχισε να κινείται, μέχρι τη στιγμή που απέκτησε την οριακή του ταχύτητα.
Κάποια στιγμή σταματάμε τον αγωγό και με κατάλληλο μηχανισμό, αυτός αρχίζει να εκτελεί απλή αρμονική ταλάντωση. Την χρονική στιγμή \(t_o=0\) η εξίσωση στιγμιαίας απομάκρυνσης του αγωγού δίνεται από την σχέση
\[x = 0.2 \cdot ημ4πt \quad (SI)\]Τα άκρα του \(Κ\) και \(Λ\) συνεχίζουν να εφάπτονται πάνω στις μεταλλικές ράβδους \(Αx\) και \(Γy\).
\(Δ_4\) Να βρείτε την διαφορά δυναμικού που εμφανίζεται στα άκρα του αγωγού \(ΚΛ\) σε συνάρτηση με τον χρόνο και να σχεδιάσετε την γραφική της παράσταση σε βαθμολογημένους άξονες για χρονική διάρκεια μιας περιόδου.
\(Δ_5\) Να υπολογιστεί ο λόγος της μέσης προς τη στιγμιαία ισχύ του εναλλασσόμενου ρεύματος που αναπτύσσεται στα άκρα του αντιστάτη \(R_1\) την χρονική στιγμή \(t=1s\).
blog comments powered by Disqus