Με ή χωρίς ατμοσφαιρική πίεση Θέμα Δ
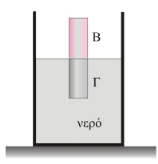
Δύο ομογενείς κύλινδροι ισορροπούν με τον άξονά τους κατακόρυφο μέσα σε δοχείο με νερό, μεγάλης επιφάνειας, όπως φαίνεται στο παραπάνω σχήμα. Ο κύλινδρος \(Γ\), μάζας \(m_Γ=0.5kg\), έχει ύψος \(h=50cm\), εμβαδό βάσης \(Α =20cm^2\) και είναι ολόκληρος βυθισμένος μέσα στο νερό. Ο κύλινδρος \(Β\) είναι ολόκληρος έξω από το νερό και έχει διαστάσεις ίδιες με τον κύλινδρο \(Γ\)
Να υπολογίσετε:
Α) την υδροστατική πίεση που επικρατεί στην κάτω βάση του κυλίνδρου \(Γ\), δηλαδή σε βάθος \(h=50cm\) από την επιφάνεια του νερού.
Β) τη δύναμη που δέχεται ο κύλινδρος \(Γ\) από το νερό εξαιτίας της υδροστατικής πίεσης, καθώς και τη δύναμη που δέχεται από τον κύλινδρο \(B\).
Γ) την πυκνότητα του κυλίνδρου \(Β\).
Αποσύρουμε απότομα τον κύλινδρο \(Β\).
Να υπολογίσετε:
Δ) την ταχύτητα του κυλίνδρου \(Γ\) τη στιγμή που εξέρχεται πλήρως από το νερό.
Να θεωρήσετε ότι δεν αλλάζει η στάθμη του νερού κατά την έξοδο του κυλίνδρου \(Γ\) απ’ αυτό και ότι η δύναμη τριβής που ασκείται από το νερό στον κύλινδρο \(Γ\), κατά την κίνησή του, είναι αμελητέα.
Δίνονται: η επιτάχυνση της βαρύτητας \(g =10 \frac{m}{s^2}\) η πυκνότητα του νερού \(ρ_ν = 1 \frac{g}{cm^3}\) και η ατμοσφαιρική πίεση \(p_{ατμ} = 10^5 \frac{N}{m^2}\).
Καλό θα είναι να μελετήσουμε πρώτα την λύση της άσκησης έτσι όπως δίνεται στην σελίδα
Επαναληπτικά θέματα » Κεφάλαιο 3ο » Επαναληπτικά προβλήματα-θέμα Δ » Πρόβλημα 2
Α)
\[P_{υδρ} = ρgh \Rightarrow P_{υδρ} = 5 \cdot 10^3 \frac{N}{m^2}\]Στην πράξη αν έχουμε ένα μανόμετρο για να μετρήσουμε την πίεση του ρευστού στην περιοχή κοντά στην κάτω βάση του κυλίνδρου \(Γ\) αυτή θα οφείλεται και στο ρευστό υγρό και στο ρευστό αέριο. Ο υπολογισμός της υδροστατικής πίεσης που γίνεται στο ερώτημα \(Α)\) αναφέρεται στην πίεση του υγρού κοντά στην κάτω βάση του κυλίνδρου όταν την συγκρίνουμε με την πίεση στην ελεύθερη επιφάνεια του υγρού. Θεωρούμαι ότι δεν έχουμε ατμοσφαιρική πίεση στην ελεύθερη επιφάνεια του υγρού οπότε η πίεση κοντά στην κάτω βάση του κυλίνδρου είναι αυτή που υπολογίζουμε. Η επιφάνεια μιας μανομετρικής κάψας κοντά στην κάτω επιφάνεια του κυλίνδρου \(Γ\) θα δεχθεί δυνάμεις από το ρεύστό υγρό οι οποίες θα είναι μεν κάθετες στην επιφάνεια της κάψας αλλά θα οφείλονται και στο ρευστό υγρό και στο ρευστό αέριο. Τελικά όλες θα προέρχονται από το βαρυτικό πεδίο της γης.
\[P_{υδρ} = P_{επιφάνεια} + ρgh \Rightarrow P_{υδρ} = 5 \cdot 10^3 \frac{N}{m^2}\]B)
Η δύναμη που δέχεται ο κυλινδρος \(Γ\) από το νερό εξαιτίας ΜΟΝΟ της υδροστατικής πίεσης είναι:
\[F_{υδρ} = P_{υδρ} \cdot A \Rightarrow F_{υδρ} = 10Ν\]Τώρα μας ζητείται να βρούμε την δύναμη που δέχεται ο κύλινδρος \(Γ\) από τον κύλινδρο \(Β\). Ακόμα και αν η διατύπωση είναι “βρείτε την δύναμη που δέχεται ο κύλινδρος \(Γ\) ΜΟΝΟ από τον κύλινδρο \(Β\)” η λύση θα πρέπει να είναι διαφορετική από την λύση που αναφέρεται στην σελίδα study4exams.
Ξεκινάμε με την ερώτηση ποια σώματα αποτελούν το περιβάλλον για τον κύλινδρο \(Γ\); Είναι το ρευστό υγρό, ο κύλινδρος \(Β\) και η γη. Άρα ο κύλινδρος \(Γ\) δέχεται τρεις δυνάμεις για τις οποίες ισχύει
\[Σ F = 0 \Rightarrow F_{ολική} = m_Γ \cdot g + N\]όπου \(Ν\) είναι η δύναμη που ασκεί ο κύλινδρος \(Β\) στον κύλινδρο \(Γ\) και λόγω του τρίτου νόμου του Νεύτωνα ισούται κατά μέτρο με την δύναμη που ασκεί ο κύλινδρος \(Γ\) στον κύλινδρο \(Β\).
\(F_{ολική}\) είναι η δύναμη που ασκεί το ρευστό (υγρό) στον κύλινδρο \(Γ\) αλλά αυτή η δύναμη δεν οφείλεται μόνο στην υδροστατική πίεση, αλλά στην συνολική πίεση που έχει το ρευστό (υγρό) στην περιοχή κοντά στην κάτω βάση του κυλίνδρου \(Γ\).
\[F_{ολική} = p_{ολική} \cdot A \Rightarrow F_{ολική} = (p_{ατμ} + p_{υδρ}) \cdot A \Rightarrow F_{ολική} = 210Ν\]και αφού κάνουμε την αντικατάσταση έχουμε για την δύναμη \(Ν\)
\[Ν = F_{ολική} - m_Γ \cdot g \Rightarrow N = 205 N\]Γ)
Αφού υπολογίσαμε την δύναμη που ασκεί ο κύλινδρος \(Β\) στον κύλινδρο \(Γ\) μπορούμε να βρούμε και την ζητούμενη πυκνότητα.
Ο κύλινδρος \(Β\) ισορροπεί άρα:
\[Σ F = 0 \Rightarrow F_{ατμ} + m_Β \cdot g = N \Rightarrow m_B = \frac{N - p_{ατμ} \cdot A}{g}\] \[ρ_Β = \frac{m_B}{V} \Rightarrow ρ_Β = \frac{N - p_{ατμ} \cdot A}{A \cdot h \cdot g} \Rightarrow ρ_Β = 500 \frac{kg}{m^3}\]Δ)
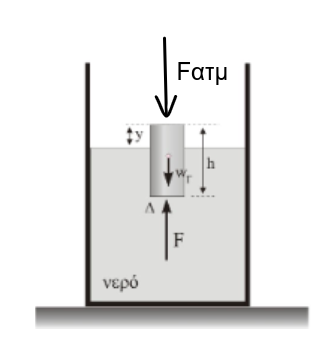
Αποσύροντας απότομα τον κύλινδρο \(Β\), ο κύλινδρος \(Γ\) αρχίζει να ανέρχεται υπό την επίδραση των δυνάμεων της μεταβλητής \(F\) του βάρους \(w_Γ\) και της κατακόρυφης δύναμης που ασκείται στην πάνω επιφάνεια του κυλίνδρου \(F_{ατμ}\) από το αέριο ρευστό. Για να βρούμε την ταχύτητα του κυλίνδρου τη στιγμή που αυτός εξέρχεται από το νερό θα εφαρμόσουμε το Θεώρημα Μεταβολής της Κινητικής Ενέργειας (Θ.Μ.Κ.Ε.) από τη θέση που ο κύλινδρος ξεκινά χωρίς αρχική ταχύτητα \(υ_ο = 0\) μέχρι τη θέση που εξέρχεται πλήρως από το νερό με ταχύτητα \(υ\).
\[ΔΚ = ΣW \Rightarrow K_{τελ} - Κ_{αρχ} = W_F + W_B + W_{F_{ατμ}}\]Πρέπει να υπολογίσουμε το έργο της μεταβλητής δύναμης \(F\).
Έστω μια τυχαία θέση στην άνοδο του κυλίνδρου. Ο κύλινδρος έχει μετατοπιστεί κατά \(y\), άρα είναι βυθισμένος κατά \(h-y\) μέσα στο νερό. Σε ένα σημείο \(Δ\) ακριβώς στη βάση του κυλίνδρου η πίεση του ρευστού είναι:
\[p_{ολική} = p_{ατμ} + p_{υδρ}) \Rightarrow p_{ολική} = p_{ατμ} + ρ \cdot g \cdot (h - y)\]και μετά τις αντικαταστάσεις υπολογίζουμε την δύναμη που ασκεί το νερό στην κάτω επιφάνεια του κυλίνδρου
\[p_{ολική} = 10^4 \cdot (10.5 - y) \Rightarrow F = 210 - 20 \cdot y \quad 0 \leq y \leq 0.5\]Για να βρούμε το έργο της \(F\) θα κάνουμε τη γραφική της παράσταση σε συνάρτηση με την μετατόπιση \(y\). To σκιασμένο εμβαδό (τραπέζιο) ισούται με το έργο της μεταβλητής δύναμης του νερού.
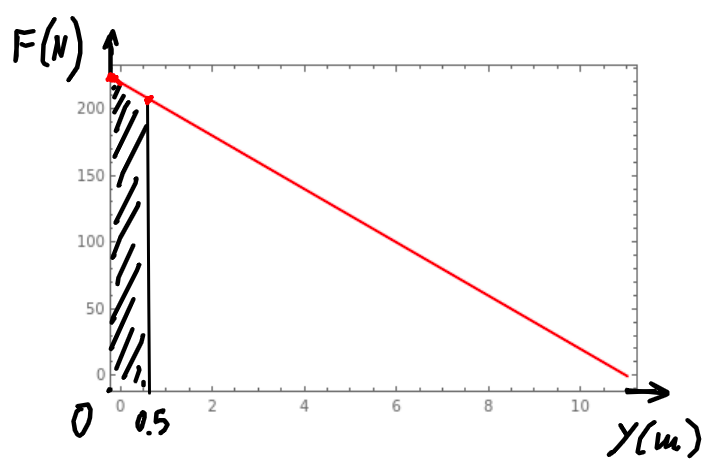
και μετά τις πράξεις στο Θ.Μ.Κ.Ε.
\[υ = 0 \frac{m}{s}\]blog comments powered by Disqus