Κρούση με ελατήριο Πλαστική και Ελαστική
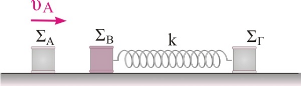
Δύο σώματα \(Σ_Β\) και \(Σ_Γ\), με μάζες \(m_β=3kg\) και \(m_Γ= 4 kg\), βρίσκονται ακίνητα πάνω σε λείο οριζόντιο επίπεδο, δεμένα στα δύο άκρα οριζόντιου ιδανικού ελατηρίου σταθεράς \(k=600 \frac{N}{m}\), το οποίο βρίσκεται στο φυσικό του μήκος. Ένα τρίτο σώμα \(Σ_Α\) μάζας \(m_Α=1kg\), κινούμενο στη διεύθυνση του άξονα του ελατηρίου με ταχύτητα \(υ_Α = 8 \frac{m}{s}\), συγκρούεται μετωπικά και πλαστικά με το σώμα \(Σ_Β\) όπως φαίνεται στο παραπάνω σχήμα.
Να υπολογίσετε:
A) την ταχύτητα του συσσωματώματος (σώμα \(Σ_Α\) και σώμα \(Σ_Β\)) αμέσως μετά τη στιγμή της πλαστικής κρούσης.
B) τις ταχύτητες που αποκτούν το συσσωμάτωμα και το σώμα \(Σ_Γ\) τη στιγμή της μέγιστης συσπείρωσης του ελατηρίου.
Γ) το ποσοστό % της αρχικής κινητικής ενέργειας του σώματος \(Σ_Α\) που μεταφέρθηκε στο ελατήριο τη στιγμή της μέγιστης συσπείρωσής του.
Δ) τον ρυθμό μεταβολής της κινητικής ενέργειας του σώματος \(Σ_Γ\), όταν το συσωμάτωμα έχει ταχύτητα \(V = \frac{3}{2} \frac{m}{s}\).
‘Απαντήσεις’
\[V_k = 2 \frac{m}{s}\] \[V'_k = 1 \frac{m}{s}\] \[Π = 12.5 \%\] \[\frac{ΔΚ}{Δt} = 30 \frac{Joule}{s}\]blog comments powered by Disqus