Μοριοδότηση 2016
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(β\)
Α2 - \(γ\)
Α3 - \(β\)
Α4 - \(δ\)
Α5: \(Σ - Λ - Σ - Λ - Λ\)
Θέμα Β
Β1 - \((ιιι)\)
α) \(\underline {τρόπος}\)
Ο ακίνητος παρατηρητής ακούει απευθείας απο τη σειρήνα του τρένου συχνότητα
\[f_1 = \frac{u_{ηχ}}{u_{ηχ} + u_s} \cdot f_s\]Ο ήχος της σειρήνας του τρένου φτάνει στον βράχο
\[f_{βραχ} = \frac{u_{ηχ}}{u_{ηχ}-u_s} \cdot f_s\]Ο παρατηρητής ακούει αυτόν τον ήχο με συχνότητα
\(f_2 = f_{βραχ}\) (ακίνητος παρατηρητής - ακίνητος βράχος)
άρα
\[\frac{f_1}{f_2} = \frac{ \frac{u_{ηχ}}{ u_{ηχ}+u_s} \cdot f_s}{\frac{u_{ηχ}} {u_{ηχ}-u_s} \cdot f_s}\] \[\frac{f_1}{f_2} = \frac{ u_{ηχ} - \frac{u_{ηχ}}{10}}{u_{ηχ} + \frac{u_{ηχ}}{10}} = \frac{9}{11}\]β) \(\underline {τρόπος}\)
Ο ακίνητος παρατηρητής ακούει απευθείας απο τη σειρήνα του τρένου μήκος κύματος
\[λ_1 = λ + u_s \cdot T_s\]Ο ήχος της σειρήνας του τρένου φτάνει στον βράχο
\[λ_{βραχ} = λ - u_s \cdot T_s\]Ο παρατηρητής ακούει αυτόν τον ήχο με μήκος κύματος
\(λ_2 = λ_{βραχ}\) (ακίνητος παρατηρητής - ακίνητος βράχος)
άρα
\[\frac{λ_1}{λ_2} = \frac{λ + u_s \cdot T_s}{λ - u_s \cdot T_s} = \frac{ \frac{u_{ηχ} +u_s}{ f_s}}{\frac{u_{ηχ}-u_s} {f_s}}\] \[\frac{λ_1}{λ_2} = \frac{u_{ηχ} + \frac{u_{ηχ}}{10} }{u_{ηχ} - \frac{u_{ηχ}}{10}} = \frac{11}{9}\] \[\frac{f_1}{f_2} = \frac{ \frac{u_{ηχ}}{λ_1}}{ \frac{u_{ηχ}}{λ_2}} = \frac{λ_2}{λ_1} =\frac{9}{11}\]Άρα η σωστή απάντηση είναι το \((ιιι)\)
Β2 - \((ι)\)
H εξίσωση του στάσιμου κύματος θα είναι
\[y = 2 A \cdot συν( \frac{2πχ}{λ} )\cdot ημ(\frac{2πt}{T})\]Το μέτρο της μέγιστης ταχύτητας ταλάντωσης \(u_{max_{M}}\) του σημείου Μ της χορδής (\(x_M = \frac{9λ}{8}\))
είναι ίσο με:
\[u_{max_{M}} = ω \cdot |A'_M| = \frac{2π}{Τ} \cdot |2A συν \frac{2π \frac{9λ}{8}}{λ}| = \frac{4π Α}{Τ} \cdot |συν \frac{9π}{4}| = \frac{2 \cdot \sqrt2 π Α}{Τ}\]Άρα η σωστή απάντηση είναι το \((ι)\)
Β3 - \((ιι)\)
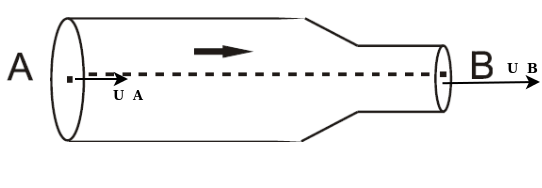
Επειδή το ρευστό είναι ασυμπίεστο και η ροή του είναι στρωτή η παροχή του σωλήνα διατηρείται σταθερή και ισχύει η εξίσωση της συνέχειας:
\[Α_Α \cdot u_A = A_B \cdot u_B \Rightarrow 2 \cdot A_B \cdot u_A = A_B \cdot u_B \Rightarrow 2 \cdot u_A = u_B\]Για ιδανικό ρευστό η κινητική ενέργεια ανά μονάδα όγκου είναι:
\[Λ = \frac{dK}{dV} = \frac{\frac{1}{2} \cdot dm \cdot u^2}{dV} = \frac{1}{2} \cdot ρ \cdot u^2\]α) \(\underline {τρόπος}\)
Εφόσον ο σωλήνας είναι οριζόντιος η εξίσωση του Bernoulli παίρνει την ακούλουθη μορφή:
\[P_A + \frac{1}{2} \cdot ρ \cdot u_A^2 = P_B + \frac{1}{2} \cdot ρ \cdot u_B^2 \Rightarrow P_A - P_B = \frac{1}{2} \cdot ρ \cdot u_B^2 - \frac{1}{2} \cdot ρ \cdot u_A^2\] \[P_A - P_B = \frac{1}{2} \cdot ρ \cdot 4 \cdot u_A^2 - \frac{1}{2} \cdot ρ \cdot u_A^2 = 4Λ - Λ = 3Λ\]β) \(\underline {τρόπος}\)
Θ.Ε.Ε. \(Α \rightarrow B\) για dt:
\[W + W_B = dK\]όπου \(W\) το έργο που προσφέρεται στο τμήμα του ρευστού από το Α στο Β από το περιβάλλον ρευστό, δηλαδή \(W = (P_A - P_B) \cdot dV\), \(W_B = 0\) και
\[dK = \frac{1}{2} \cdot dm \cdot u_B^2 - \frac{1}{2} \cdot dm \cdot u_A^2\]Τελικά
\[(P_A - P_B) \cdot dV = \frac{1}{2} \cdot dm \cdot u_B^2 - \frac{1}{2} \cdot dm \cdot u_A^2 \Rightarrow P_A - P_B = \frac{1}{2} \cdot \frac{dm}{dV} \cdot u_B^2 - \frac{1}{2} \cdot \frac{dm}{dV} \cdot u_A^2\] \[(P_A - P_B) = \frac{1}{2} \cdot ρ \cdot u_B^2 - \frac{1}{2} \cdot ρ \cdot u_A^2 = \frac{1}{2} \cdot ρ (2u_A)^2 - \frac{1}{2} \cdot ρ \cdot u_A^2 = 3 \cdot \frac{1}{2} \cdot ρ \cdot u_A^2 = 3Λ\]Άρα η σωστή απάντηση είναι το \((ιι)\)
Θέμα Γ
Λείο τεταρτοκύκλιο ΑΓ
R = 5m
μ = 0.5
ΓΔ = \(S_1 = 3.6 m\)
μάζες \(m_2 = 3 \cdot m_1\)
και \(u_2 = 4 \frac{m}{s}\)
Γ1
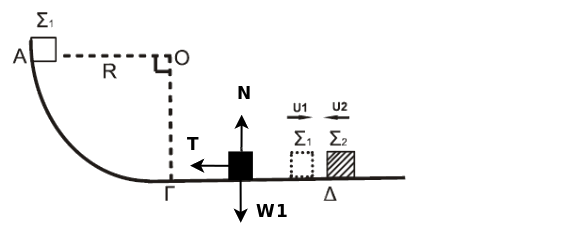
Α.Δ.Μ.Ε. \((Α,Γ)(m_1)\)
\[Κ_Α + U_A = K_Γ + U_Γ \Rightarrow 0 + m_1 \cdot g \cdot R = \frac{1}{2} \cdot m_1 \cdot u_o^2 + 0 \Rightarrow u_o = \sqrt{2 \cdot g \cdot R} \Rightarrow u_o = 10 \frac{m}{s}\]Γ2
α) \(\underline {τρόπος}\)
Θ.Μ.Κ.Ε. \(Γ \rightarrow Δ (m_1)\)
\[K_Δ - Κ_Γ = W_T \Rightarrow \frac{1}{2} \cdot m_1 \cdot u_1^2 - \frac{1}{2} \cdot m_1 \cdot u_o^2 = -μ \cdot m_1 \cdot g \cdot S_1 \Rightarrow u_1 = 8 \frac{m}{s}\]β) \(\underline {τρόπος}\)
\[ΣF = m \cdot α \Rightarrow T = m \cdot α \Rightarrow μ \cdot m \cdot g = m \cdot α \Rightarrow α = 5 \frac{m}{s^2}\] \[S_1 = u_o \cdot t - \frac{1}{2} \cdot α \cdot t^2 \Rightarrow 5 \cdot t^2 - 20 \cdot t + 7.2 =0\] \[t = \frac{20 \pm 16}{10} = \left\{ \begin{array}{ c l } 0.4 & \\ 3.6, & απορρίπτεται \end{array} \right.\] \[u_1 = u_o - α \cdot t \Rightarrow u_1 = 8 \frac{m}{s}\]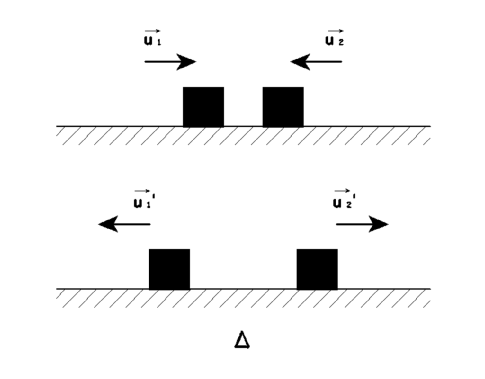
α) \(\underline {τρόπος}\)
Τα \(m_1\), \(m_2\) συγκρούονται στο Δ κεντρικά και ελαστικά. Από ΑΔΟ και ΔΚΕ προκύπτει:
\[u_1' = \frac{2m_2 \cdot(-u_2)+(m_1-m_2) \cdot u_1}{m_1+m_2} = -10 \frac{m}{s} \Rightarrow |u_1'| = 10 \frac{m}{s}\] \[u_2' = \frac{2m_1 \cdot u_1 + (m_2-m_1) \cdot (-u_2)}{m_1+m_2} = +2 \frac{m}{s} \Rightarrow |u_2'| = 2 \frac{m}{s}\]β) \(\underline {τρόπος}\)
ΑΔΟ
\[\vec{p_{πριν}} = \vec{p_{μετά}} \Rightarrow m_1 \cdot u_1 - m_2 \cdot u_2 = -m_1 \cdot u_1' + m_2 \cdot u_2' \Rightarrow u_1' = 4 + 3 \cdot u_2'\]ΔΚΕ
\[\frac{1}{2} \cdot m_1 \cdot u_1^2 + \frac{1}{2} \cdot m_2\cdot u_2^2 = \frac{1}{2} \cdot m_1 \cdot u_1'^2 + \frac{1}{2} \cdot m_2 \cdot u_2'^2 \Rightarrow 112 = u_1'^2 + 3\cdot u_2'^2\]Αντικαθιστώντας την προηγούμενη σχέση φτάνουμε στην δευτεροβάθμια
\[u_2'^2 + 2\cdot u_2' - 8 = 0\] \[u_2' = \frac{-2 \pm 6}{2} = \left\{ \begin{array}{ c l } 2 & \\ -4, & απορρίπτεται \end{array} \right.\]οπότε
\[u_1' = 4 + 3\cdot u_2' \Rightarrow u_1' = 10 \frac{m}{s}\]Γ3
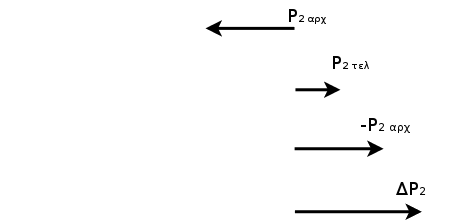
μάζα \(m_2 = 3kg\)
\[\vec{ΔP_2} = \vec{P_{2τελ}} - \vec{P_{2αρχ}} = \vec{P_{2τελ}} + (- \vec{P_{2αρχ}})\] \[ΔP_2 = m_2 \cdot u'_2 - (-m_2 \cdot u_2) = m_2 \cdot (u'_2 + u_2) \Rightarrow ΔP_2 = 18 kg \cdot \frac{m}{s}\]Γ4
Το ποσοστό επι τοις εκατό της μεταβολής της κινητικής ενέργειας του \(m_1\) κατά την κρούση είναι:
\[Π(\%) = \frac{ΔΚ_1}{Κ_{1αρχ}} \cdot 100 \% = \frac{\frac{1}{2} \cdot m_1 \cdot (u_1^{'2} - u_1^2)}{ \frac{1}{2}\cdot m_1 \cdot u_1^2} \cdot 100 \% = (\frac{u_1^{'2}}{u_1^2} - 1)\cdot 100 \% = 56.25 \%\]Θέμα Δ
ΒΓ Λείο κεκλιμένο δάπεδο με γωνία κλίσης \(φ = 30^ο\)
σώμα μάζας \(m = 1kg\)
σταθερά ελατηρίου \(k = 100 \frac{N}{m}\)
μάζα κυλίνδρου \(Μ = 2kg\)
ακτίνα κυλίνδρου \(R = 0.1m\)
ροπή αδράνειας \(I_{cm} = \frac{1}{2} \cdot M \cdot R^2\)
σταθερά \(g = 10 \frac{m}{s^2}\)
Δ1
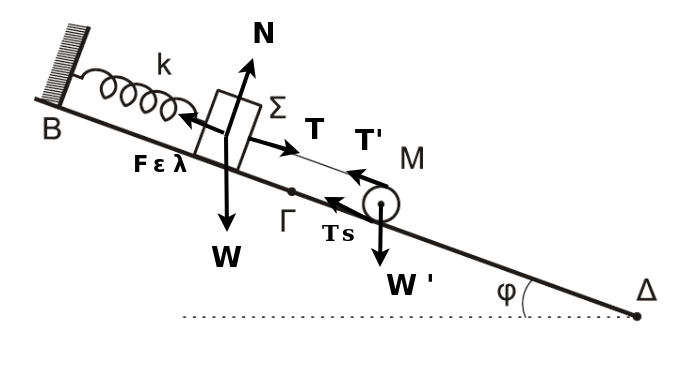
Ο κύλινδρος ισορροπεί
\[ΣF_x = 0 \Rightarrow T' + T_{στ} - M \cdot g \cdot ημφ = 0\] \[Στ = 0 \Rightarrow T' \cdot R - T_{στ} R = 0\] \[2T' = M \cdot g \cdot ημφ \Rightarrow T' = 5N\]\(Τ' = Τ\) (3ος Ν. Νεύτωνα, νήμα αβαρές μη εκτατό)
m ισορροπεί
\[F_{ελ} - m \cdot g \cdot ημφ - Τ =0\] \[F_{ελ} = k \cdot Δl\]Άρα
\[Δl = \frac{m \cdot g \cdot ημφ +Τ}{k} = 0.1m\]Δ2
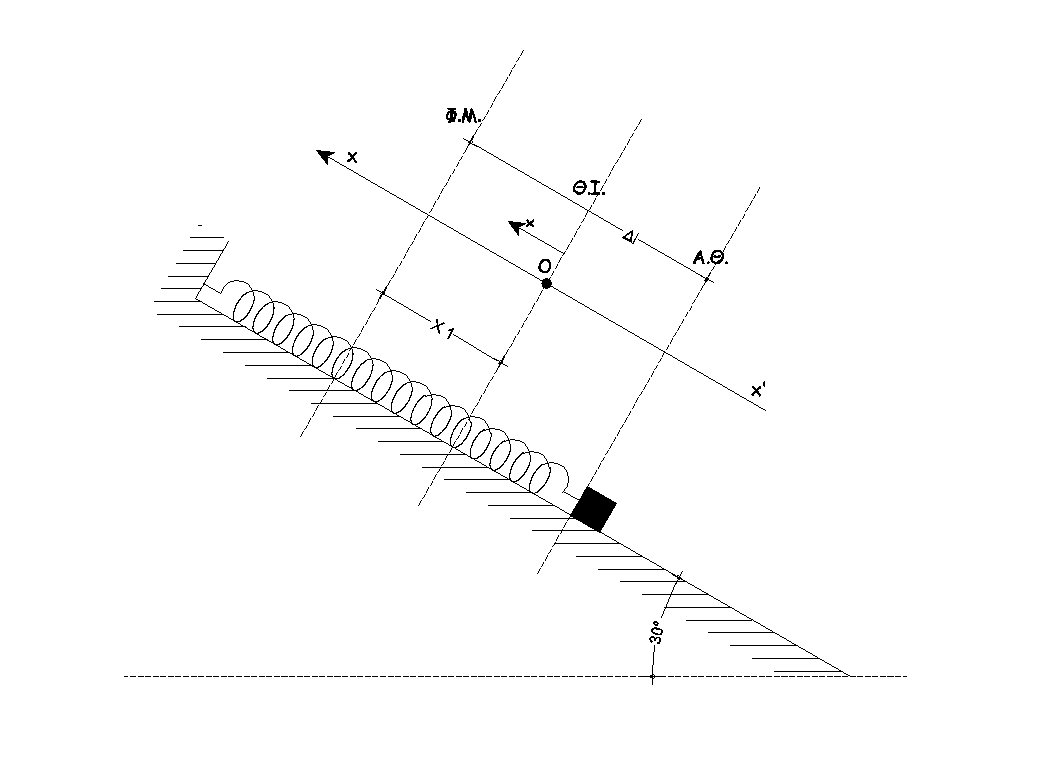
Αφού κοπεί το νήμα τo m εκτελεί απλή αρμονική ταλάντωση με θέση ισορροπίας το Ο
\[D = k = m \cdot ω^2 \Rightarrow ω = 10 \frac{r}{s}\]Για την \(ΘΙ(O):\)
\[F_{ελ(ο)} - m \cdot g \cdot ημφ = 0 \Rightarrow k \cdot x_1 - m \cdot g \cdot ημφ = 0 \Rightarrow x_1 = 0.05m\]Την \(t=0\) το \(m\) βρίσκεται στο Γ με \(u = 0\) άρα το πλάτος ταλάντωσης είναι:
\[Α = Δl - x_1 \Rightarrow A = 0.05m\] \[x_Γ = -Α\]Η χρονική συνάρτηση της απομάκρυνσης του σώματος από την θέση ισορροπίας είναι
\[x = A \cdot ημ (ω \cdot t + φ_ο)\]Tην \(t=0\):
\[-Α = Α \cdot ημ φ_ο \Rightarrow ημ φ_ο = ημ \frac{3π}{2} \Rightarrow φ_ο = 2kπ + \frac{3π}{2}\] \[0 \leq φο < 2π\]Άρα \(φο = \frac{3π}{2} rad\)
Επομένως \(x = 0.05 ημ(10t + \frac{3π}{2})\) στο \(SI\)
α) \(\underline {τρόπος}\)
\[F_{επ} = - D \cdot x = - 100 \cdot 0.05 ημ (10t + \frac{3π}{2}) \Rightarrow F_{επ} = -5 \cdot ημ(10t + \frac{3π}{2}) (SI)\]β) \(\underline {τρόπος}\)
\[F_{επ} = ΣF = F_{ελ} - m \cdot g \cdot ημφ = k(x_1 - x) - m \cdot g \cdot ημφ = kx_1 - kx - m \cdot g \cdot g \cdot ημφ\] \[F_{επ} = -k\cdot x \Rightarrow F_{επ} = -5 \cdot ημ(10t + \frac{3π}{2}) (SI)\]Δ3
Μόλις κοπεί το νήμα ο κύλινδρος εκτελεί κύλιση χωρίς ολίσθηση στο κεκλιμένο δάπεδο ΓΔ. Το σώμα αφού εκτελέσει Ν περιστροφές έχει αποκτήσει γωνιακή ταχύτητα \(ω\).
\[Ν = \frac{12}{π} = \frac{Δθ}{2π} \Rightarrow Δθ = 24 rad\]Η στροφορμή που θα έχει ο κύλινδρος θα είναι
\[L = I_{cm} \cdot ω\] \[I_{cm} = \frac{1}{2} M \cdot R^2 = 0.01 kg m^2\]Για την εύρεση του ω:
α) \(\underline {τρόπος}\)
Κύλιση χωρίς ολίσθηση \(\rightarrow\) η τριβή δεν μετατοπίζει το σημείο εφαρμογής της αφού κάθε στιγμή ασκείται σε διαφορετικό σημείο του κυλίνδρου δηλαδή είναι στατική τριβή.
Στην παραπάνω κίνηση διατηρείται η μηχανική ενέργεια του κυλίνδρου
\[Κ_{αρχ} +U_{αρχ} = Κ_{τελ} +U_{τελ} \Rightarrow 0 + M \cdot g \cdot h = (\frac{1}{2} \cdot M \cdot u_{cm}^2 + \frac{1}{2} \cdot I_{cm} \cdot ω^2) + 0\] \[h = x_{cm} \cdot ημφ\] \[x_{cm} = {Δθ}{R}\]άρα \(h = 24 \cdot 0.1 \cdot \frac{1}{2} \Rightarrow h = 1.2m\)
\[u_{cm} = ω \cdot R\]αντικαθιστώντας έχουμε
\[2 \cdot 10 \cdot 1.2 = \frac{1}{2} \cdot 2 \cdot ω^2 \cdot 0.01 + \frac{1}{2} \cdot 0.01 \cdot ω^2 \Rightarrow ω = 40 \frac{r}{s}\]οπότε
\[L = 0.01 \cdot 40 \Rightarrow L = 0.4 \frac{kg \cdot m^2}{s}\]β) \(\underline {τρόπος}\)
Μεταφορική:
\[M \cdot g \cdot ημφ - Τ_{στ} = Μ \cdot α_{cm}\]Στροφική:
\[Τ_{στ} \cdot R = \frac{1}{2} \cdot M \cdot R^2 \cdot α_{γων}\]Κύλιση χωρίς ολίσθηση:
\[α_{cm} = α_{γων} \cdot R\]Άρα
\[Μ \cdot g \cdot ημφ = \frac{3}{2} \cdot M \cdot α_{cm} \Rightarrow α_{cm} = \frac{10}{3} \frac{m}{s^2}\] \[α_{γων} = \frac{100}{3} \frac{r}{s^2}\] \[Δθ = \frac{1}{2} \cdot α_{γων} \cdot t^2 \Rightarrow t = 1.2 s\] \[ω = α_{γων} \cdot t = 40 \frac{r}{s}\]Δ4
για \(t' = 3s\)
α) \(\underline {τρόπος}\)
\[\frac{dK}{dt} = \frac{dK}{dt}_{μετ} + \frac{dK}{dt}_{περ} = ΣF \cdot u_{cm} + Στ \cdot ω = Μ \cdot α_{cm} \cdot u_{cm} + I \cdot α_{γων} \cdot ω\] \[\frac{dK}{dt} = Μ \cdot α_{cm}^2 \cdot t' + I \cdot α_{γων}^2 \cdot t' = 100 \frac{J}{s}\]β) \(\underline {τρόπος}\)
\[\frac{dK}{dt} = \frac{dK}{dt}_{μετ} + \frac{dK}{dt}_{περ} = (W_x - T_{στ}) \cdot u_{cm} + (T_{στ} \cdot R) \cdot ω\]ΚΧΟ:
\[u_{cm} = ω \cdot R\]άρα
\[\frac{dK}{dt} = W_x \cdot u_{cm} - T_{στ} u_{cm} + T_{στ} u_{cm} = W_x \cdot u_{cm} \Rightarrow \frac{dK}{dt} = 100 \frac{J}{s}\]γ) \(\underline {τρόπος}\)
\[Κ = \frac{1}{2} \cdot M \cdot u^2 + \frac{1}{2} \cdot I \cdot ω^2 = \frac{1}{2} \cdot M \cdot ω^2 \cdot R^2 + \frac{1}{2} \cdot \frac{1}{2} \cdot M \cdot R^2 ω^2 = \frac{3}{4} \cdot M \cdot R^2 ω^2\]Αφού \(ω = α_{γων} \cdot t\)
\[K = \frac{3}{4} \cdot M \cdot R^2 \cdot α_{γων}^2 \cdot t^2 = \frac{100}{6} \cdot t^2 (SI)\]Ο ρυθμός μεταβολής της κινητικής ενέργειας είναι:
\[\frac{dK}{dt} = \frac{100}{6} \cdot 2 \cdot t = \frac{100}{3} \cdot t (SI)\]και για \(t=3s\)
\[\frac{dK}{dt} = 100 \frac{J}{s}\]δ) \(\underline {τρόπος}\)
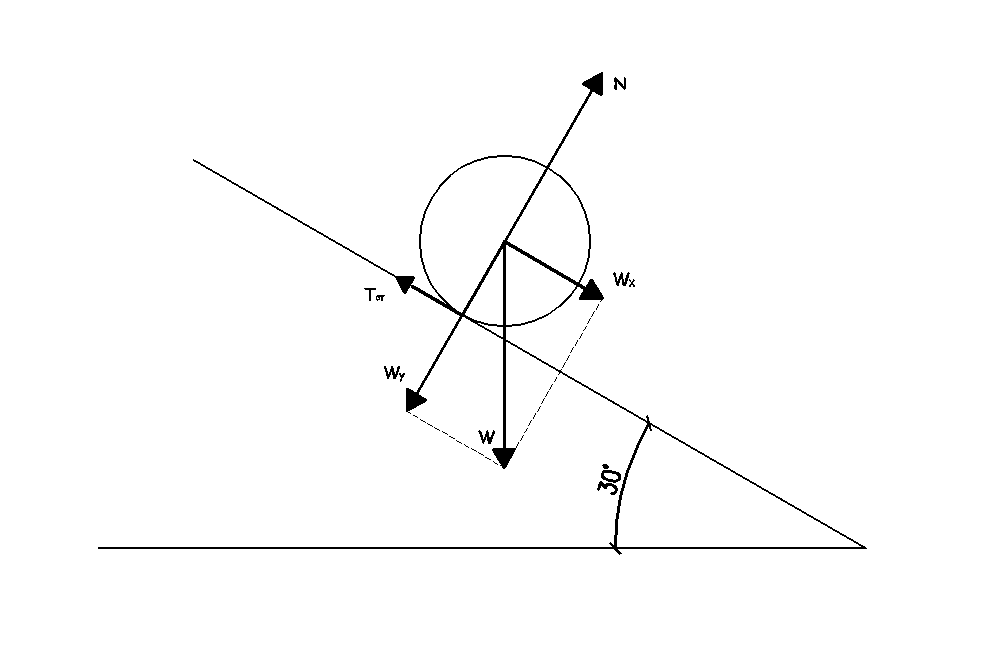
Έστω \(Α\) το σημείο επαφής του κυλίνδρου με το κεκλιμένο επίπεδο. Θεωρούμε στιγμιαίο άξονα περιστροφής οριζόντιο που διέρχεται από το σημείο Α. Ο κύλινδρος εκτελεί μόνο περιστροφική κίνηση γύρω από τον στιγμιαίο άξονα περιστροφής.
Θεώρημα παραλλήλων αξόνων
\[Ι_Α = Ι_{cm} + M \cdot R^2 \Rightarrow I_A = \frac{1}{2} \cdot M \cdot R^2 + M \cdot R^2 \Rightarrow I_A = \frac{3}{2} \cdot M \cdot R^2\] \[Στ = Ι_Α \cdot α_{γων} \Rightarrow M \cdot g \cdot ημφ \cdot R = \frac{3}{2} \cdot M \cdot R^2 \cdot α_{γων} \Rightarrow α_{γων} = \frac{100}{3} \frac{rad}{s^2}\] \[\frac{dK}{dt} = Στ \cdot ω = Ι_Α \cdot α_{γων} \cdot α_{γων} \cdot t = \frac{3}{2} \cdot M \cdot R^2 \cdot α_{γων}^2 \cdot t \Rightarrow \frac{dK}{dt} = 100 \frac{J}{s}\]Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus