Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2016
Λεπτή ομογενής και ισοπαχής ράβδος μάζας \(m=3kg\) και μήκους \(L=1m\), μπορεί να περιστρέφεται χωρίς τριβές γύρω από οριζόντιο άξονα που περνά από το μέσο της O. Η ράβδος έχει στερεωμένο στο ένα της άκρο σώμα \(Σ_1\) μάζας \(m_1 =3kg\) μικρών διαστάσεων και στο άλλο άκρο σώμα \(Σ_2\) μάζας \(m_2 =1kg\) επίσης μικρών διαστάσεων. Η ράβδος ισορροπεί σε οριζόντια θέση όταν στο σώμα \(Σ_1\) προσκρούει κατακόρυφη φλέβα νερού όπως δίνεται στο σχήμα. Το νερό έχει πυκνότητα \(ρ=10^3 \frac{kg}{m^3}\) και προέρχεται από στόμιο διατομής \(Α_1\) το οποίο βρίσκεται στον πυθμένα δοχείου διατομής \(A=1 m^2\) . Πάνω από την επιφάνεια του νερού στο δοχείο υπάρχει έμβολο μάζας \(Μ=200kg\) που μπορεί να κινείται χωρίς τριβές. Όταν η ράβδος ισορροπεί σε οριζόντια θέση (σχήμα 1) το ύψος του νερού μέσα στο δοχείο είναι \(h=0.6m\) και το έμβολο βρίσκεται στο ίδιο οριζόντιο επίπεδο με την ράβδο.
Δίνονται: Το νερό θεωρείται ιδανικό ρευστό, ενώ οι αντιστάσεις από τον αέρα θεωρούνται αμελητέες. Η ταχύτητα του εμβόλου θεωρείται επίσης αμελητέα. Η ροπή αδράνειας της ράβδου μάζας \(m\) γύρω από τον άξονα περιστροφής είναι \(I_ρ = \frac{1}{12} \cdot m \cdot L^2\). Επίσης \(g=10 \frac{m}{s^2}\) και \(P_{atm} =10^5 Pa\).
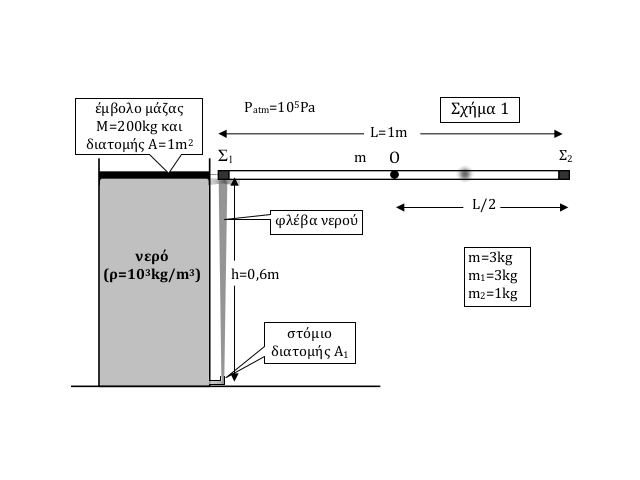
1. Να βρεθεί το μέτρο της ταχύτητας εξόδου \(υ_o\) του νερού από το στόμιο.
2. Να βρεθεί δύναμη που ασκεί η φλέβα στο σώμα \(Σ_1\) όταν η ράβδος ισορροπεί οριζόντια.
3. Να βρεθεί η παροχή της φλέβας όταν η ράβδος ισορροπεί οριζόντια. Θεωρείστε ότι κατά την πρόσκρουση στοιχειώδους μάζας νερού στο \(Σ_1\) , η στοιχειώδης μάζα ακινητοποιείται στιγμιαία.
4. Κάποια στιγμή διακόπτουμε την φλέβα. Να βρεθεί η δύναμη που δέχεται η ράβδος από τον άξονα περιστροφής τη στιγμή που η φλέβα νερού έχει μόλις σταματήσει να προσκρούει στο σώμα \(Σ_1\) και η ράβδος είναι ακόμη οριζόντια.
Δίνεται ότι το κέντρο μάζας του συστήματος ράβδου και σωμάτων \(Σ_1\), \(Σ_2\) βρίσκεται μεταξύ του σημείου \(Ο\) και του \(Σ_1\) και απέχει απόσταση \(d= \frac{1}{7}m\) από το σημείο \(Ο\).
5. Να βρεθεί η δύναμη που δέχεται η ράβδος από τον άξονα περιστροφής όταν αυτή βρεθεί σε κατακόρυφη θέση.
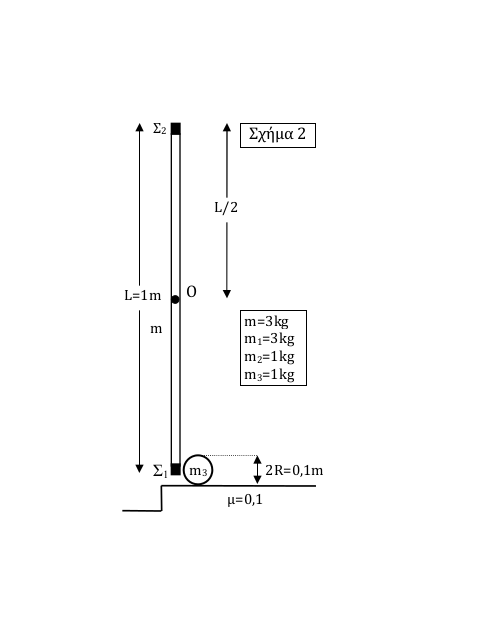
6. Όταν η ράβδος περνά από την κατακόρυφη θέση, το άκρο στο οποίο βρίσκεται το σώμα \(Σ_1\) συγκρούεται με αρχικά ακίνητο λεπτό δακτύλιο μάζας \(m_3 =1kg\) και ακτίνας \(R=0.05m\) που βρίσκεται στο επίπεδο κίνησης της ράβδου όπως δίνεται στο σχήμα 2. Αμέσως μετά την κρούση ο δακτύλιος αποκτά μόνο μεταφορική ταχύτητα, ενώ η γωνιακή ταχύτητα της ράβδου έχει μέτρο \(ω_1 =3.2 \frac{rad}{s}\) και κατεύθυνση ίδια με αυτήν που είχε πριν την κρούση. Αν ο συντελεστής τριβής μεταξύ δακτυλίου και εδάφους είναι \(μ=0.1\) να βρεθεί το διάστημα που διανύει ο δακτύλιος σε χρονικό διάστημα \(Δt=2s\) αμέσως μετά την σύγκρουση.
Απάντηση:
blog comments powered by Disqus