Επαναληπτικές 2015
Ομογενής τροχαλία ισορροπεί έχοντας το νήμα τυλιγμένο γύρω της πολλές φορές. Η μία άκρη του νήματος είναι στερεωμένη στην οροφή Ο και η άλλη στο σώμα Σ, το οποίο ισορροπεί κρεμασμένο από κατακόρυφο ιδανικό ελατήριο σταθεράς \(k=40\frac{N}{m}\), που είναι στερεωμένο στην οροφή, όπως φαίνεται στο Σχήμα
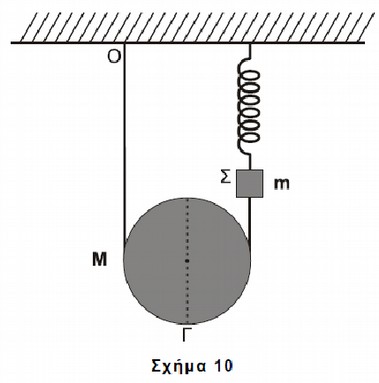
Η μάζα της τροχαλίας είναι \(M=1,6kg\) και η ακτίνα της \(R=0,2m\). Η ροπή αδράνειας της τροχαλίας, ως προς άξονα που είναι κάθετος στο επίπεδό της και ο οποίος διέρχεται από το κέντρο μάζας της, δίνεται από τη σχέση \(I=\frac{1}{2} \cdot M \cdot R^2\). Το σώμα Σ θεωρείται σημειακό αντικείμενο μάζας \(m=1,44kg\). Το νήμα και το ελατήριο έχουν αμελητέες μάζες.
Δ1. Να υπολογίσετε τη δύναμη που ασκεί το ελατήριο στο σώμα Σ.
Κάποια χρονική στιγμή κόβουμε το νήμα που συνδέει την τροχαλία με το σώμα Σ, και το σώμα Σ αρχίζει να εκτελεί απλή αρμονική ταλάντωση. Τη χρονική στιγμή που μηδενίζεται η στιγμιαία ταχύτητα του σώματος Σ, για πρώτη φορά, το κέντρο μάζας της τροχαλίας έχει μετατοπιστεί κατακόρυφα κατά απόσταση h. Η αντίσταση του αέρα θεωρείται αμελητέα και το νήμα δεν ολισθαίνει στο αυλάκι της τροχαλία.
Δ2. Να υπολογίσετε την κατακόρυφη μετατόπιση \(h\) της τροχαλίας.
Δ3. Να γράψετε την εξίσωση της απομάκρυνσης του σώματος Σ σε συνάρτηση με το χρόνο, θεωρώντας ότι η τιμή \(t=0s\) αντιστοιχεί στη χρονική στιγμή που κόπηκε το νήμα και ότι η φορά απομάκρυνσης του σώματος Σ προς τα πάνω είναι θετική.
Δ4. Να υπολογίσετε το μέτρο της ταχύτητας του κάτω άκρου Γ της τροχαλίας, όταν το κέντρο μάζας της τροχαλίας έχει μετατοπιστεί κατακόρυφα κατά απόσταση h.
Δίνονται: η επιτάχυνση της βαρύτητας \(g=10 \frac{m}{s^2},π=\sqrt{10}\) και \(π^2=10\) (προσεγγιστικά).
Απάντηση:
Δ1. Για το σημειακό αντικείμενο μάζας \(m\) το περιβάλλον αποτελούν τα σώματα: γη, ελατήριο και το νήμα που το συνδέει με την τροχαλία. Άρα στο σημειακό αντικείμενο ασκούνται τρεις δυνάμεις: η έλξη της γης, η δύναμη του ελατηρίου και η τάση του νήματος. Γι’ αυτές τις δυνάμεις ισχύει:
\[{F}_{ελ} = m_1 \cdot g + T_1\]Για την τροχαλία το περιβάλλον αποτελούν τα σώματα: γη, το νήμα που συνδέει την τροχαλία με το σημειακό αντικείμενο και το νήμα που συνδέει την τροχαλία με την οροφή Ο. Άρα στην τροχαλία ασκούνται τρεις δυνάμεις: η έλξη της γης και οι δύο τάσεις των νημάτων. Γι’ αυτές τις δυνάμεις ισχύει:
\[T_1 + T_2 = M \cdot\] \[Στ=0 \Rightarrow T_2 \cdot R − T_1 \cdot R = 0 \Rightarrow T_2 = T_1\]και κάνοντας τις πράξεις υπολογίζουμε \(Fελ=22,4N\)
Δ2. Αφού κόψουμε το νήμα το σημειακό αντικείμενο εκτελεί απλή αρμονική ταλάντωση, η περίοδος της οποίας υπολογίζεται ως:
\[T= 2 \cdot π \sqrt {\frac{m_1}{k}} \Rightarrow T=1.2s\]Την χρονική στιγμή που μηδενίζεται στιγμιαία η ταχύτητα του σώματος Σ, αυτό βρίσκεται στην θέση \(x=+A\), ενώ την χρονική στιγμή \(t=0\) αυτό ξεκίνησε από την θέση \(x=−A\), δηλαδή πέρασε χρόνος ίσος με την μισή περίοδο της ταλάντωσης, έτσι
\[t=\frac{T}{2} \Rightarrow t=0.6s\]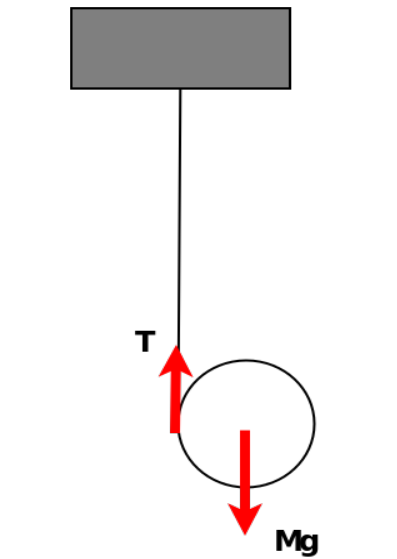
Για την τροχαλία ο δεύτερος νόμος του Νεύτωνα μας δίνει:
\[ΣF = M\cdot α_{cm} \Rightarrow M \cdot g − T = M \cdot α_{cm}\]ενώ για την στροφική κίνηση έχουμε
\[Στ = I \cdot α_{γων} \Rightarrow T \cdot R = \frac{1}{2} \cdot M \cdot R^2 \cdot α_{γων}\]Λύνοντας το παραπάνω σύστημα και αντικαθιστώντας όπου \(α_{γων}=α_{cm} \cdot R\) βρίσκουμε για την επιτάχυνση του κέντρου μάζας \(α_{cm}= \frac{20}{3} \frac{m}{s^2}\) οπότε για την κατακόρυφη μετατόπιση της τροχαλίας έχουμε:
\[h=\frac{1}{2}\cdot α_{cm} \cdot t^2 \Rightarrow h=1.2m\]Δ3. Για το σώμα Σ που εκτελεί απλή αρμονική ταλάντωση μπορούμε να υπολογίσουμε το πλάτος ταλάντωσης ως εξής:
\[A=x_2−x_1\]όπου \(x_1\) είναι η απόσταση της θέσης ισορροπίας από το φυσικό μήκος του ελατηρίου και \(x_1\) η απόσταση της ακραίας θέσης από το φυσικό μήκος του ελατηρίου. Αυτές οι αποστάσεις βρίσκονται από την ισορροπία του σώματος Σ μετά το κόψιμο του νήματος και από την αρχική ισορροπία πριν το κόψιμο του νήματος. Δηλαδή:
\[ΣF=0 \Rightarrow F_{ελ}=m \cdot g \Rightarrow x_1=\frac{14.4}{40}\] \[F_{ελ}=k \cdot x_2 \Rightarrow x_2= \frac{22.4}{40}\] \[A=0.2m\]H αρχική φάση υπολογίζεται από την πληροφορία ότι το σώμα Σ την χρονική στιγμή \(t=0\) βρίσκεται στην θέση \(x=−A\) αφού η φορά απομάκρυνσης του σώματος προς τα πάνω θεωρείται θετική. Η κυκλική συχνότητα δίνεται από την σχέση
\[ω=\sqrt{\frac{k}{m}} \Rightarrow ω= \frac{5\cdotπ}{3}\]οπότε η εξίσωση απομάκρυνσης του σώματος Σ σε συνάρτηση με τον χρόνο είναι:
\[x=0.5ημ(\frac{5π}{3} \cdot t+ \frac{3π}{2})\]Δ4. Το κάτω άκρο της τροχαλίας συμμετέχει ταυτόχρονα σε δύο κινήσεις. Σε μία μεταφορική και σε μια περιστροφική. Για την μεταφορική έχουμε:
\[u_{cm}=α_{cm} \cdot t \Rightarrow u_{cm}=4 \frac{m}{s}\]ενώ για την περιστροφική πρέπει πρώτα να υπολογίσουμε την γωνιακή επιτάχυνση, έπειτα την γωνιακή ταχύτητα και τέλος την γραμμική ταχύτητα. Δηλαδή:
\[α_{γων}=α_{cm}R \Rightarrow α_{γων}= \frac{100}{3} \frac{r}{s^2}\] \[ω=α_{γων} \cdot t \Rightarrow ω=20 \frac{r}{s}\] \[u_{γραμ}=v \cdot R \Rightarrow u_{γραμ}=4 \frac{m}{s}\]H ταχύτητα που ζητείται είναι το διανυσματικό άθροισμα των δύο προηγούμενων ταχυτήτων. Δηλαδή:
\[u_Γ=4 \cdot \sqrt2 \frac{m}{s}\]και με διεύθυνση που σχηματίζει γωνία \(45^ο\) με την κατακόρυφο μιας και \(u_{cm}\) και \(u_{γραμ}\) είναι όχι μόνο κάθετα αλλά και ίσα κατά μέτρο διανύσματα.
blog comments powered by Disqus