Ρευστά σχολικό
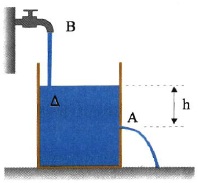
Στο δοχείο \(Δ\) πέφτει συνέχεια νερό από τη βρύση \(Β\) όπως φαίνεται στο επόμενο σχήμα. Το δοχείο δε μπορεί να γεμίσει επειδή χύνεται νερό από το πλευρικό άνοιγμα \(Α\). Αν η παροχή της βρύσης είναι \(22 \frac{cm^3}{s}\) και το εμβαδόν του ανοίγματος \(1 cm^2\), να βρείτε σε ποιο ύψος \(h\) πάνω από το σημείο \(Α\) θα σταθεροποιηθεί η ελεύθερη επιφάνεια. Δίνεται \(g = 10 \frac{m}{s^2}\)
Απάντηση:
Σύμφωνα με την εφαρμογή \(3-2\), θεώρημα Torricelli, η ταχύτητα με την οποία ρέει το νερό από το άνοιγμα \(Α\) θα είναι
\[υ_A = \sqrt{2 \cdot g \cdot h }\]Η παροχή του ανοίγματος είναι
\[Π=A_A \cdot υ_A = A_A \cdot \sqrt{2 \cdot g \cdot h }\]Για να διατηρείται η στάθμη του νερού στο δοχείο σταθερή πρέπει η παροχή της βρύσης να είναι ίση με την παροχή του ανοίγματος.
\[Π = Π_A = A_A \cdot \sqrt{2 \cdot g \cdot h }\]και έτσι
\[h = \frac{Π^2}{2 \cdot g \cdot A_A^2} \Rightarrow h = 0.00242 m\]Flow of Fluid through a Hole in a Tank from the Wolfram Demonstrations Project by Rana Gordji
blog comments powered by Disqus