Doppler σχολικό
Ένας μοτοσικλετιστής που βρίσκεται σε απόσταση \(d = 400m\) από μια ακίνητη ηχητική πηγή συχνότητας \(540Hz\) αρχίζει να κινείται προς αυτή με σταθερή επιτάχυνση. Η συχνότητα του ήχου που αντιλαμβάνεται τη στιγμή που φτάνει στην πηγή είναι \(603,5 Hz\). Να υπολογίσετε την επιτάχυνσή του και να παραστήσετε γραφικά τη συχνότητα που αντιλαμβάνεται ο μοτοσυκλετιστής σε συνάρτηση με το χρόνο. Η ταχύτητα του ήχου στον αέρα είναι \(340m/s\).
Η συχνότητα του ήχου που ακούει ο κινούμενος παρατηρητής δίνεται από τη σχέση
\[f_A = \frac{υ+υ_Α}{υ} \cdot f_S\]άρα η ταχύτητα με την οποία κινείται κάθε στιγμή ο παρατηρητής δίνεται από τη σχέση
\[υ_Α = \frac{f_A - f_S}{f_S} \cdot υ\]Θέτουμε \(f_A = 603,5Hz\) και βρίσκουμε την ταχύτητα του παρατηρητή τη στιγμή που φτάνει στην πηγή \(υ_Α = 40 \frac{m}{s}\)
Ο παρατηρητής κάνει ομαλά επιταχυνόμενη κίνηση χωρίς αρχική ταχύτητα οπότε
\[υ_A = a \cdot t\] \[d = \frac{1}{2}\cdot a \cdot t^2\]Απαλείφουμε το χρόνο από τις παραπάνω εξισώσεις και βρίσκουμε
\[a = 2 \frac{m}{s^2}\]Για την συχνότητα που αντιλαμβάνεται ο παρατηρητής μέχρι την πηγή έχουμε την σχέση
\[f_A = \frac{υ+ a \cdot t}{υ} \cdot f_S \Rightarrow f_A = 540 + \frac{54}{17} \cdot t\]H συνάρτηση έχει πεδίο ορισμού
\[0 \le t < 20s\]H συχνότητα που αντιλαμβάνεται ο παρατηρητής την στιγμή που βρίσκεται ακριβώς στην πηγή είναι \(f_A = f_S = 540 Hz\), ενώ η συχνότητα που αντιλαμβάνεται αφού διέλθει από την πηγή δίνεται από την σχέση
\[f_A = \frac{υ - a \cdot t}{υ} \cdot f_S \Rightarrow f_A = 540 - \frac{54}{17} \cdot t\]H συνάρτηση έχει πεδίο ορισμού
\[20 \le t < 170s\]και η γραφική παράσταση και για τους δυο κλάδους της συνάρτησης φαίνεται στο σχήμα. H φυσική σημασία του μηδενισμού της συχνότητας που αντιλαμβάνεται ο παρατηρητής είναι η εξής: Την χρονική στιγμή \(t=170s\), o παρατηρητής έχει αποκτήσει ταχύτητα
\[υ = a \cdot t \Rightarrow υ=340 \frac{m}{s}\]δηλαδή σπάει το φράγμα του ήχου και κινείται με μεγαλύτερη ταχύτητα και γι αυτό το λόγο μηδενίζεται η συχνότητα που αντιλαμβάνεται.
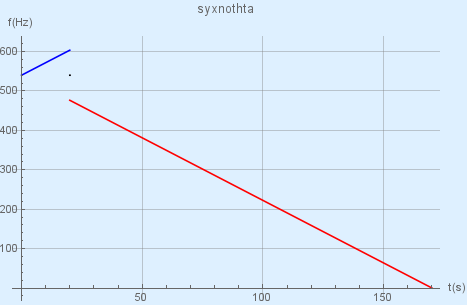
και ο κώδικας σε mathematica
f[t] := 540 + 54t/17
h[t] := 540
g[t] := 540 - 54t/17
Show[{Plot[f[t], {t, 0, 20}, PlotStyle -> Blue],
Plot[h[t], {t, 20, 20.1}, PlotStyle -> Black],
Plot[g[t], {t, 20, 170}, PlotStyle -> Red]},
PlotRange -> All,
GridLines -> Automatic,
Background -> LightBlue,
PlotLabel -> "syxnothta",
AxesLabel -> {"t(s)","f(Hz)"},
AxesOrigin -> {0, 0},
Filling -> Automatic]
blog comments powered by Disqus