Επαναληπτικές 2013
Σε κινούμενο τρένο (1) με ταχύτητα \(u_1\) υπάρχει ηχητική πηγή που εκπέμπει ήχο συχνότητας \(f_s\) για χρονικό διάστημα \(Δt_s\). Τρένο (2) κινείται με ταχύτητα \(u_2\) αντίθετης φοράς και την στιγμή \(t_o = 0\) απέχει από το τρένο (1) απόσταση d. Στο τρένο (1) υπάρχει συσκευή ανίχνευσης των ανακλώμενων στο τρένο (2) ηχητικών κυμάτων. Δίνεται ότι ο ανακλώμενος ήχος στο τρένο (2) έχει την ίδια συχνότητα με τον προσπίπτοντα σε αυτόν ήχο.
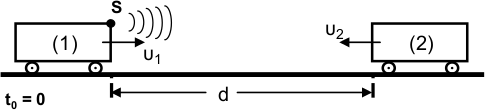
Γ1. Αν \(f_1\) είναι η συχνότητα του ήχου που ανιχνεύει η συσκευή, να δείξετε ότι
\[f_1 = \frac{u+u_2}{u-u_2} \cdot \frac{u+u_1}{u-u_1} \cdot f_s\]Δίνονται: ταχύτητα ήχου \(u = 340 \frac{m}{s}\), \(f_s = 1900Hz\), \(u_1 = u_2 = 20 \frac{m}{s}\), \(Δt_s = 0,81s\).
Γ2. Αν τη χρονική στιγμή \(t_1 = 6,8 s\) η συσκευή αρχίζει να ανιχνεύει τον ανακλώμενο ήχο, να βρεθεί η απόσταση d που είχαν τα τρένα τη χρονική στιγμή \(t_o = 0\).
Γ3. Ποια χρονική στιγμή \(t_2\) η συσκευή ανίχνευσης των ανακλώμενων κυμάτων σταματά να καταγράφει τον ανακλώμενο ήχο;
Απάντηση:
Γ1. Η συχνότητα του ήχου που φτάνει στο τρένο (2) βρίσκεται από την σχέση
\[f_2 = \frac{u+u_2}{u-u_1} \cdot f_s\]και η συχνότητα του ήχου που φτάνει στο τρένο (1) είναι
\[f_1 = \frac{u+u_1}{u-u_2} \cdot f_2 \Rightarrow f_1 = \frac{u+u_2}{u-u_2} \cdot \frac{u-u_1}{u+u_1} /cdot f_s\]Γ2. Έστω \(Δt_3\) ο χρόνος που ο ήχος κάνει να φτάσει στο τρένο (2) και \(Δt_4\) ο χρόνος που ο ανακλώμενος ήχος κάνει να φτάσει στον ανιχνευτή του τρένου (1). Τότε ισχύουν
\[d = 340 \cdot Δt_3 + 20 \cdot Δt_3 \Rightarrow d = 360 \cdot Δt_3\]ακολουθώντας την ίδια λογική έχουμε
\[d = 340 \cdot Δt_4 + 20 \cdot Δt_4 + 40 \cdot Δt_3 \Rightarrow d = 360 \cdot Δt_4 + 40 \cdot Δt_3\]με την βοήθεια των προηγούμενων σχέσεων βρίσκουμε τα \(Δt_3 = 3,6s\) και \(Δt_4 = 3,2 s\), οπότε η απόσταση είναι \(d = 1296m\)
Γ3. Κάνοντας χρήση την σχέση που αποδείξαμε στο πρώτο ερώτημα έχουμε μετά τις πράξεις \(f = \frac{81}{64} \cdot f_s\). O αριθμός των μεγίστων που εκπέμπει η συσκευή είναι ίσος με τον αριθμό των μεγίστων που ανιχνεύει οπότε για την χρονική διάρκεια ανίχνευσης βρίσκουμε
\(Δt_1 = \frac{64}{81} \cdot Δt_s\) και μετά τις πράξεις \(Δt_1 = 0,64s\). Έτσι η ζητούμενη χρονική στιγμή είναι
\[t_2 = t_1 + Δt_1 \Rightarrow t_2 = 7,44 s\]blog comments powered by Disqus