Ράβδοι συνδεδεμένες
Δύο ράβδοι είναι συνδεδεμένες στο άκρο τους Α και σχηματίζουν σταθερή γωνία 60ο μεταξύ τους, όπως φαίνεται στο Σχήμα 7. Οι ράβδοι είναι διαφορετικές μεταξύ τους, αλλά κάθε μία είναι ομογενής. Το σύστημα των δύο ράβδων μπορεί να περιστρέφεται γύρω από άρθρωση, που είναι στερεωμένη σε τοίχο, στο άκρο Α, χωρίς τριβές. Το σύστημα αφήνεται να περιστραφεί υπό την επίδραση της βαρύτητας από τη θέση του Σχήματος 7, όπου η ράβδος \(l_1\) είναι οριζόντια, με αρχική ταχύτητα μηδέν.
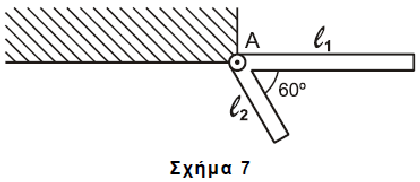
Δίνεται ότι τα μήκη των δύο ράβδων είναι \(l_1=4m\) και \(l_2=2m\), ενώ η μάζα της ράβδου \(l_2\) είναι \(m_2=10kg\).
Γ1. Να υπολογίσετε τη μάζα \(m_1\) της ράβδου μήκους \(l_1\), εάν το σύστημα αποκτά τη μέγιστη γωνιακή ταχύτητα τη χρονική στιγμή που οι δύο ράβδοι σχηματίζουν ίσες γωνίες με την κατακόρυφο, όπως φαίνεται στο επόμενο σχήμα 8.
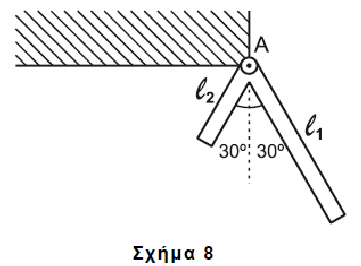
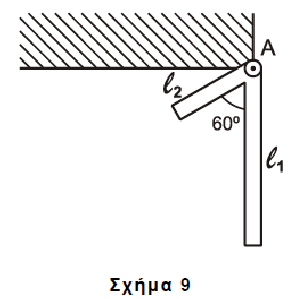
Γ2. Να υπολογίσετε τη μάζα \(m_1\) της ράβδου μήκους \(l_1\), εάν το σύστημα σταματά στιγμιαία, όταν η ράβδος μήκους \(l_1\) φτάνει στην κατακόρυφη θέση που φαίνεται στο Σχήμα 9.
Γ3. Να υπολογίσετε τη γωνιακή επιτάχυνση του συστήματος των δύο ράβδων του ερωτήματος Γ2 στη θέση που απεικονίζεται στο Σχήμα 9.
Γ4. Να υπολογίσετε τον ρυθμό μεταβολής της στροφορμής της ράβδου μήκους \(l_2\) του ερωτήματος Γ2 στη θέση που απεικονίζεται στο Σχήμα 9.
Δίνονται: η επιτάχυνση της βαρύτητας \(g=10 \frac{m}{s^2}\), η ροπή αδρανείας ράβδου μήκους \(l\) και μάζας \(m\) που περιστρέφεται γύρω από το άκρο της Α, \(I=\frac{1}{3} \cdot m \cdot l^2\) , και ότι \(\sqrt3 = 1,7\) (προσεγγιστικά).
Γ1. Περιβάλλον για το σύστημα των δύο ράβδων είναι ο τοίχος και η γη. Αυτό σημαίνει ότι στο σύστημα ασκούνται τρεις δυνάμεις - αλληλεπιδράσεις. Η δύναμη της άρθρωσης και η έλξη της γης σε κάθε ράβδο. Η κίνηση που κάνει το σύστημα των δύο ράβδων είναι αρχικά επιταχυνόμενη και μετά από την θέση στο σχήμα 8 η κίνηση γίνεται επιβραδυνόμενη. Το σύστημα αποκτά την μέγιστη γωνιακή ταχύτητα στο σχήμα 8, όπου η μηδενίζεται η γωνιακή επιτάχυνση.
\[Στ=0 \Rightarrow m_2 \cdot g \cdot \frac{l_2}{2} \cdot ημ30 = m_1 \cdot g \cdot \frac{l_1}{2} \cdot ημ30\]και κάνοντας τις πράξεις υπολογίζουμε την μάζα \(m_1=5kg\).
Γ2. Θεωρούμε επίπεδο μηδενικής δυναμικής ενέργειας το επίπεδο που διέρχεται από το κέντρο μάζας της ράβδου μήκους \(l_1\). Εφαρμόζουμε την αρχή διατήρησης της μηχανικής ενέργειας από την θέση Ι του συστήματος των δύο ράβδων στο σχήμα 7 στην θέση ΙΙ στο σχήμα 9.
\[{E^I}_{M} = E^{II}_{M} \Rightarrow K^I+U^I=K^{II}+U^{II}\] \[0+m_1 \cdot g \cdot \frac{l_1}{2} + m_2 \cdot g \cdot (\frac{l_1}{2}− \frac{l_2}{2} \cdot ημ60)= 0 + m_2 \cdot g \cdot (\frac{l_1}{2}− \frac{l_2}{2} \cdot συν60)\]και κάνοντας τις πράξεις βρίσκουμε για την μάζα \(m_1=74kg\)
Γ3. Για το σχήμα 9 η γωνιακή επιτάχυνση του συστήματος των ραβδών βρίσκεται ως εξής:
\[Στ_{ολ}=I_{ολ} \cdot a_{γων} \Rightarrow a_{γων} = \frac{Στ_{ολ}}{I_{ολ}}\] \[I_{ολ}=I_1+I_2=\frac{1}{3} \cdot m_1 \cdot {l_1}^2 +\frac{1}{3} \cdot m_2 \cdot {l_2}^2\]κάνοντας τις πράξεις βρίσκουμε για την συνολική ροπή αδράνειας \(Iολ= \frac{68}{3}kg\cdot m^2\), και για την γωνιακή επιτάχυνση \(α_{γων}=− \frac{15}{4} \frac{rad}{s^2}\).
Γ4. Για τον ρυθμό μεταβολής της στροφορμής της ράβδου μήκους \(l_2\) έχουμε
\[\frac{ΔL}{Δt} = I_2 \cdot α_{γων} \Rightarrow \frac{ΔL}{Δt} = \frac{1}{3} \cdot m_2 \cdot {l_2}^2 \cdot α_{γων}\]και κάνοντας τις αντικαταστάσεις έχουμε τελικά
\[\frac{ΔL}{Δt} =−50 \frac{kg \cdot m^2}{s^2}\]blog comments powered by Disqus