Συμβολή Άσκηση του σχολικού βιβλίου
Δύο σύγχρονες πηγές \(Π_1\) και \(Π_2\) δημιουργούν στην επιφάνεια ενός υγρού κύματα, με πλάτος \(Α = 3mm\) και περίοδο \(T = 0,4s\). Η ταχύτητα των κυμάτων είναι \(5 \frac{m}{s}\). Ένα μικρό κομμάτι φελλού βρίσκεται σε κάποιο σημείο της επιφάνειας, σε αποστάσεις \(r_1=6m\) και \(r_2=5,5m\) από τις πηγές. Η κίνηση του φελλού είναι αποτέλεσμα της συμβολής των δύο κυμάτων. Να περιγράψετε την κίνησή του και να κάνετε την γραφική παράστασης της κατακόρυφης απομάκρυνσης συναρτήση του χρόνου.
Απάντηση:
Από τα δεδομένα της άσκησης έχουμε:
\[ω = \frac{2π}{Τ} \Rightarrow ω = 5π \frac{rad}{s}\] \[υ = \frac{λ}{Τ} \Rightarrow λ = υ \cdot T \Rightarrow λ = 2m\]Το κύμα από την πηγή \(Π_1\) φθάνει στο σημείο Σ την χρονική στιγμή
\[t_1 = \frac{r_1}{υ} \Rightarrow t_1 = 1,2 s\]ενώ από την πηγή \(Π_2\) φθάνει στο σημείο Σ σε χρονική διάρκεια
\[t_2 = \frac{r_2}{υ} \Rightarrow t_2 = 1,1 s\]To κύμα που φθάνει από την πηγή \(Π_1\) έχει εξίσωση
\[y_1 = 3 \cdot ημ(5πt - 6π) = 3 \cdot ημ[5π(t-1,2)+0]\]εξίσωση που ισχύει για \(t \ge 1,2s\), ενώ το κύμα που φθάνει στο σημείο Σ από την πηγή \(Π_2\) έχει εξίσωση
\[y_2 = 3 \cdot ημ(5πt - 5,5π) = 3 \cdot ημ[5π(t-1,1)+0]\]εξίσωση που ισχύει για \(t \ge 1,1s\). Για την συμβολή των κυμάτων ισχύει η εξίσωση \(y = y_1 + y_2\) και μετά τις πράξεις
\[y = 3 \cdot \sqrt{2} \cdot ημ(5πt - \frac{11,5π}{2}) = 3 \cdot \sqrt{2} \cdot ημ[5π(t-1,2 ) + \frac{π}{4}]\]εξίσωση που ισχύει για \(t \ge 1,2s\).
Άρα συνοπτικά για την κίνηση του φελλού έχουμε την παρακάτω χρονική συνάρτηση
\[y_Σ = 0\]για χρόνο \(0 \le t < 1,1s\)
\[y_Σ = 3 \cdot ημ[5π(t-1,1)+0]\]για χρόνο \(1,1s \le t < 1,2s\) και
\[y_Σ = 3 \cdot \sqrt{2} \cdot ημ[5π(t-1,2 ) + \frac{π}{4}]\]για χρόνο \(t \ge 1,2s\)
Η γραφική παράστασης της προηγούμενης συνάρτησης φαίνεται στο παρακάτω σχήμα.
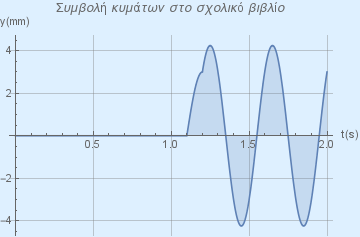
και ο κώδικας σε mathematica
Plot[Piecewise[{ {0, 0<t< 1.1},
{3*Sin[5*Pi(t-1.1)], 1.1<t<1.2},
{3*Sqrt[2]*Sin[5*Pi(t-1.2)+Pi/4], 1.2<t} }],
{t, 0, 2},
PlotLegends ->"Expressions",
PlotRange -> All,
PlotLabel -> "\Symboli kymaton sto sxoliko biblio",
Background -> LightBlue,
GridLines -> Automatic,
AxesLabel -> {"t(s)", "y(mm)"},
Filling -> Automatic]
blog comments powered by Disqus