S.T.E.M.

Ευθύγραμμη ομαλή κίνηση με φωτοπύλες

Ο σκοπός αυτού του φύλλου εργασίας είναι να σε βοηθήσει να μελετήσεις την ευθύγραμμη ομαλή κίνηση. Θα χρησιμοποιήσεις αεροτράπεζα και οκτώ φωτοπύλες για τη μέτρηση του χρόνου διέλευσης (mode \(F_1\)), συνδεδεμένες όπως δείχνεται στην παρακάτω εικόνα.

σχήμα

Δεδομένα

Η απόσταση μεταξύ των φωτοπυλών είναι \(d=10cm=0,1m\)

Το πάχος της μεταλικής προεξοχής του ιππέα είναι \(L=4.9cm=0.049m\)

Οδηγίες

  1. Οριζοντίωσε την αεροτράπεζα χρησιμοποιώντας το αλφάδι.

  2. Τοποθέτησε τις φωτοπύλες πάνω στην αεροτράπεζα σε ίσες αποστάσεις \(d\).

  3. Εκτόξευσε τον ιππέα με μικρή αρχική ταχύτητα και κατέγραψε τους χρόνους διέλευσης.

Υπολογισμοί

Για κάθε φωτοπύλη υπολόγισε την στιγμιαία ταχύτητα του ιππέα με τον τύπο

\[υ_i= \frac{L}{t_i}\]

Υπολόγισε τον χρόνο κίνησης από φωτοπύλη σε φωτοπύλη με τον τύπο

\[Δt_i=\frac{d}{υ_i}\]

Ο συνολικός χρόνος κίνησης από την χρονική στιγμή που ο ιππέας διέρχεται από την πρώτη φωτοπύλη \(t_0=0\) έως τη χρονική στιγμή που περνά από την n-ιοστή δίνεται από τη σχέση

\[T_i = T_{i-1} + t_i + Δt_i\]

Συμπλήρωσε τον πίνακα στην επόμενη εικόνα

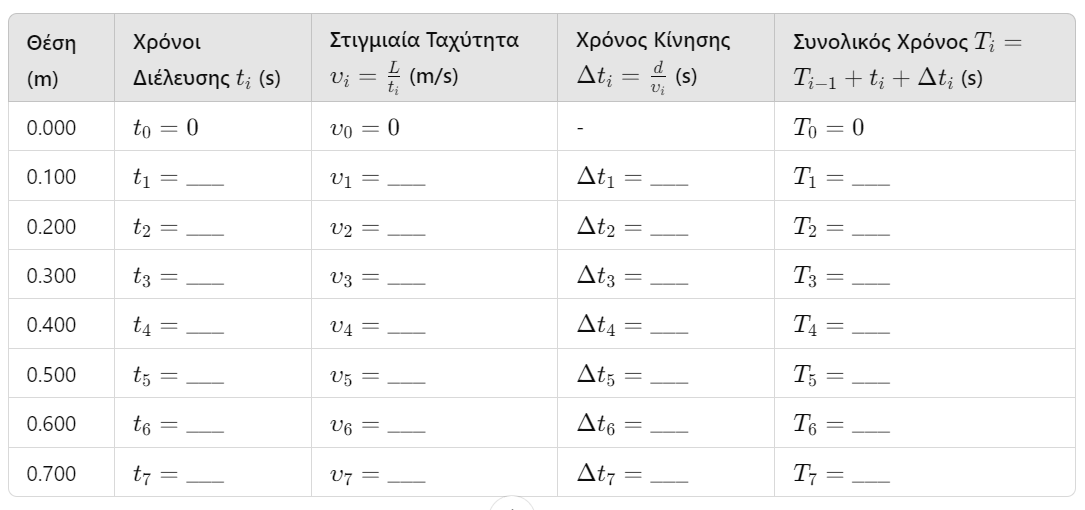
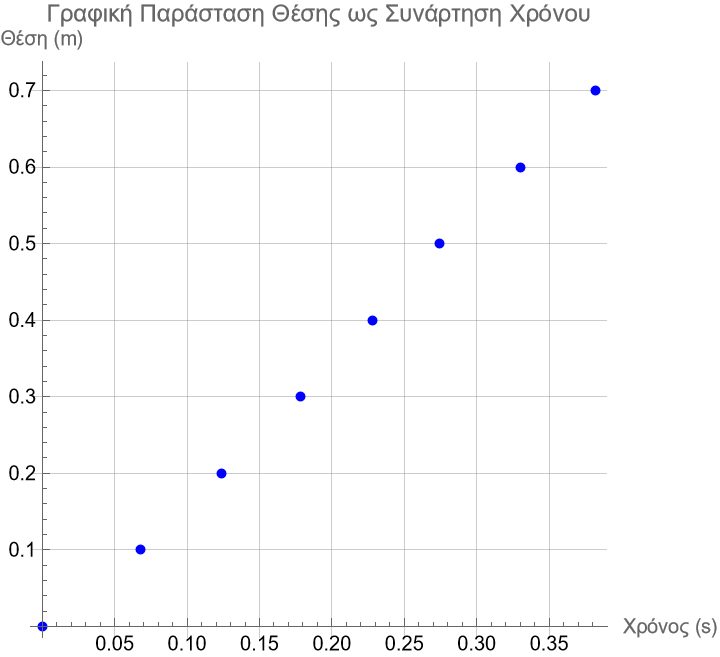
σχήμα

Με τα δεδομένα που συμπλήρωσες τον πίνακα (στήλες Θέση \(x(m)\), και Συνολικός χρόνος \(t(s)\)) και με τη βοήθεια του milimetre φτιάξε τη γραφική παράσταση \(x=f(t)\)

Η διαδικασία υπολογισμού των χρόνων κίνησης \(Δt_i\) θα σε βοηθήσει να κατανοήσεις πως οι αλλαγές στην ταχύτητα επηρεάζουν το χρόνο κίνησης από φωτοπύλη σε φωτοπύλη.

Συζήτησε με τους συμμαθητές σου τι βρήκες και πως μπορείς αλλάζοντας κάποιες παραμέτρους να επαναλάβεις το πείραμα για να εξερευνήσεις πως οι μεταβολές επηρεάζουν τους υπολογισμούς.

Μπορείς να χρησιμοποιήσεις τον παρακάτω κώδικα στο \(Mathematica\) ή στην ιστοσελίδα Wolfram Alpha για να δημιουργήσεις τη γραφική παράσταση

	(* Δεδομένα θέσεων και συνολικών χρόνων *)
		x = {0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7};
		t = {0.000, 0.068, 0.124, 0.178, 0.228, 0.274, 0.330, 0.382};
	(* Δημιουργία γραφικής παράστασης *)
	ListPlot[Transpose[{t, x}], 
		 PlotStyle -> {Blue, PointSize[Medium]}, 
		 AxesLabel -> {"Χρόνος (s)", "Θέση (m)"}, 
		 AspectRatio -> 1, 
		 PlotRange -> All,
		 PlotLabel -> "Γραφική Παράσταση Θέσης ως Συνάρτηση Χρόνου",
		 GridLines -> Automatic]

Η εικόνα με τα δικά σου δεδομένα θα μοιάζει κάπως έτσι:

σχήμα

blog comments powered by Disqus

Published

28 September 2024

Category

Άσκηση

Tags