Επαναληπτικές εξετάσεις 2024
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(α\)
Α3 - \(β\)
Α4 - \(δ\)
Α5: \(Σ - Σ - Λ - Λ - Σ\)
Θέμα Β
B1-\((ii)-2-6\)

Το σημείο \(Β\) για πρώτη φορά τη χρονική στιγμή \(t_1 = \frac{9T}{4}\) έχει \(y_B = +A\) Η χρονική διάρκεια κίνησής του από τη θέση ισορροπίας του μέχρι την ακραία θέση είναι \(\frac{T}{4}\). Άρα
\[t_{εκκ(Β)} = \frac{9T}{4} - \frac{T}{4} = 2T\] \[t_{εκκ(Β)} = \frac{x_B}{υ_Δ} \Rightarrow x_B = υ_Δ \cdot 2T \Rightarrow x_B = \frac{λ}{Τ} \cdot 2T \Rightarrow x_B = 2λ\] \[β) \underline {τρόπος}\]Εξίσωση κύματος \(y = A \cdot ημ(\frac{2πt}{T}-\frac{2πx}{λ})\)
Για το σημείο \(Β\) ισχύει την χρονική στιγμή \(t_1=\frac{9T}{4}\), \(y_B=+A\) άρα από την εξίσωση κύματος
\[+Α= Α \cdot ημ(\frac{2πt}{T}\cdot \frac{9T}{4}-\frac{2πx_B}{λ}) \Rightarrow \frac{9π}{2}-\frac{2πx_B}{λ} =2kπ +\frac{π}{2}\]Για πρώτη φορά \(k=0\)
\[\frac{9}{2} -\frac{2x_B}{λ} =0+\frac{1}{2} \Rightarrow 4= \frac{2x_B}{λ} \Rightarrow x_B = 2λ\]Την χρονική στιγμή \(t_1=\frac{9T}{4}\) για \(x \ge 0\) η διαταραχή έφτασε μέχρι \(x_1\)
\[υ_Δ = \frac{x_1}{t_1} \Rightarrow \frac{λ}{T}= \frac{x_1}{\frac{9T}{4} } \Rightarrow x_1=\frac{9λ}{4}\] \[y = \begin{cases} Α ημ (\frac{2πt}{T}\cdot \frac{9T}{4}-\frac{2πx_B}{λ})=Α \cdot ημ(\frac{9π}{2}-\frac{2πx}{λ}) \quad 0 \le x \le \frac{9λ}{4} \\\ 0 \quad \frac{9λ}{4} < x \end{cases}\]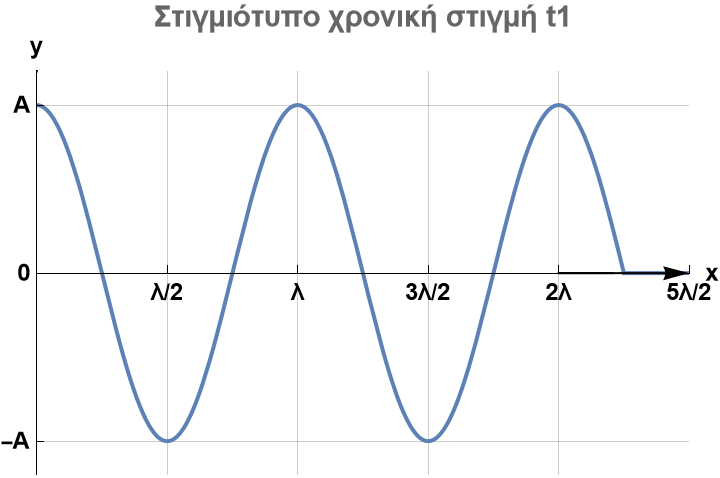
Άρα μεταξύ των σημείων \(Ο\) και \(Β\) τα σημεία που είναι ακίνητα \((y=\pm A)\) είναι 3.
άρα σωστό το ii)
B2-\((i)-2-6\)
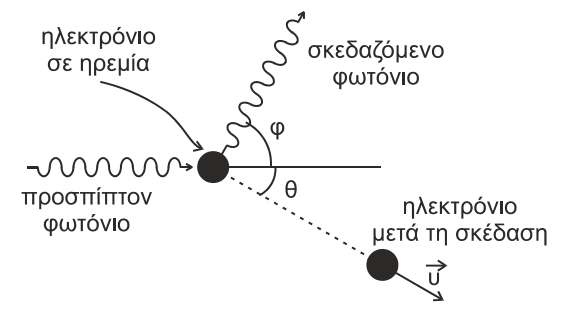
Ισχύει η αρχή διατήρησης της ορμής \(\vec{p}=\vec{p'}+\vec{p_e}\) και η υπόθεση του \(De Broglie\) σύμφωνα με την οποία \(p= \frac{h}{λ}\)
Αρχή διατήρησης της ορμής κατά τον οριζόντιο άξονα \(x\)
\[p = p' \cdot συνφ + p_e \cdot συνθ \Rightarrow \frac{h}{λ} = \frac{h}{λ'} \cdot \frac{1}{2} + p_e \cdot \frac{\sqrt3}{2}\]Παρόμοια κατά τον κατακόρυφο άξονα \(y\)
\[0=p' \cdot ημφ - p_e \cdot ημθ \Rightarrow \frac{h}{λ'} \cdot \frac{\sqrt3}{2} = p_e \cdot \frac{1}{2}\]Λύνοντας το σύστημα των δύο εξισώσεων προκύπτει \(λ'=2 \cdot λ\)
οπότε από το φαινόμενο Compton έχουμε:
\[λ' - λ = \frac{h}{m \cdot c}(1 - συν60^ο) \Rightarrow 2λ - λ = \frac{h}{m \cdot c}(1 - \frac{1}{2}) \Rightarrow λ = \frac{h}{2m c}\]άρα σωστό το i)
B3-\(α-(i), β-(iii)-3-6\)
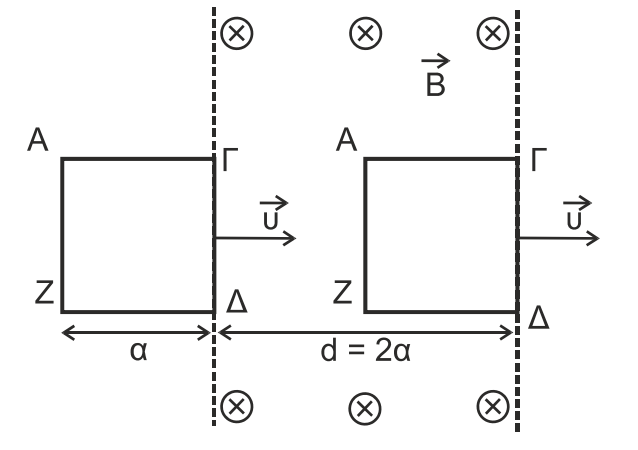
Κατά την είσοδο αφού \(x = υt\) ισχύουν
\[0 \le x < α, \quad 0 \le t < \frac{α}{υ}\]Κατά την παραμονή
\[α \le x < d, \quad \frac{α}{υ} \le t < \frac{d}{υ}=t_1\]Η μαγνητική ροή που διέρχεται από το συρμάτινο τετράγωνο πλαίσιο δίνεται από τη συνάρτηση
\[Φ = \begin{cases} Β \cdot α \cdot x = Β \cdot α \cdot υ \cdot t \quad 0 \le t < \frac{α}{υ} \\\ B \cdot α^2=σταθ \quad \frac{α}{υ} \le t < \frac{d}{υ}=t_1 \end{cases}\]Το μέτρο της επαγωγικής τάσης που αναπτύσεται στο πλαίσιο υπολογίζεται από τη σχέση
\[Ε_{επ} = \frac{ΔΦ}{Δt} \Rightarrow E_{επ} = Β \cdot α \cdot \frac{Δx}{Δt} \Rightarrow E_{επ} = Β \cdot α \cdot υ\]Άρα η συνάρτηση για την επαγωγική τάση που εμφανίζεται στο πλαίσιο είναι
\[Ε_{επ} = \begin{cases} Β \cdot α \cdot υ=σταθ \quad 0 \le t < \frac{α}{υ} \\\ 0(Φ=σταθ) \quad \quad \frac{α}{υ} \le t < \frac{d}{υ}=t_1 \end{cases}\]Ενώ η συνάρτηση για την ένταση του ηλεκτρικού ρεύματος που διαρρέει το πλαίσιο είναι
\[Ι = \begin{cases} \frac{Ε_{επ}}{R}=Β \cdot α \cdot υ=σταθ \quad 0 < t < \frac{α}{υ} \\\ 0 \frac{α}{υ} < t < \frac{d}{υ}=t_1 \end{cases}\]H δύναμη \(Laplace\) στα άκρα του αγωγού \(ΓΔ\) υπολογίζεται από τη σχέση
\[F_L = B \cdot I \cdot l = \frac{B^2α^2υ}{R}=σταθ\]και η συνάρτηση για τη δύναμη είναι
\[F = \begin{cases} \frac{B^2α^2υ}{R} \quad 0 \le t < \frac{α}{υ} \\\ 0 \quad \frac{α}{υ} \le t < \frac{d}{υ}=t_1 \end{cases}\]Οι δυνάμεις \(Laplace\) που ασκούνται από το μαγνητικό πεδίο στους αγωγούς \(ΑΓ\) και \(ΖΔ\) καθώς το πλαίσιο εισέρχεται μέσα στο μαγνητικό πεδίο είναι ίσου μέτρου και αντίθετης φοράς, άρα η συνολική δύναμη που ασκείται στο πλαίσιο είναι μόνο η δύναμη που ασκείται στον αγωγό \(ΓΔ\) κατά τη χρονική διάρκεια που διαρκεί η είσοδος του πλαισίου στο μαγνητικό πεδίο. Όσο το πλαίσιο βρίσκεται εξ’ ολοκλήρου στο μαγνητικό πεδίο δεν ασκείτα καμία δύναμη.
άρα σωστό το \(i\)
Το έργο της δύναμης για την κίνηση του πλαισίου είναι
\[W_{F_{(0-t_1)}} = W_{F_{(0-\frac{α}{υ})}} + W_{F_{(\frac{α}{υ}-t_1)}} = F \cdot Δx +0 = \frac{B^2 α^2 υ}{R}\cdot α=\frac{B^2 α^3 υ}{R}\]άρα σωστό το \(iii\)
Θέμα Γ
Γ1-\((5)\)
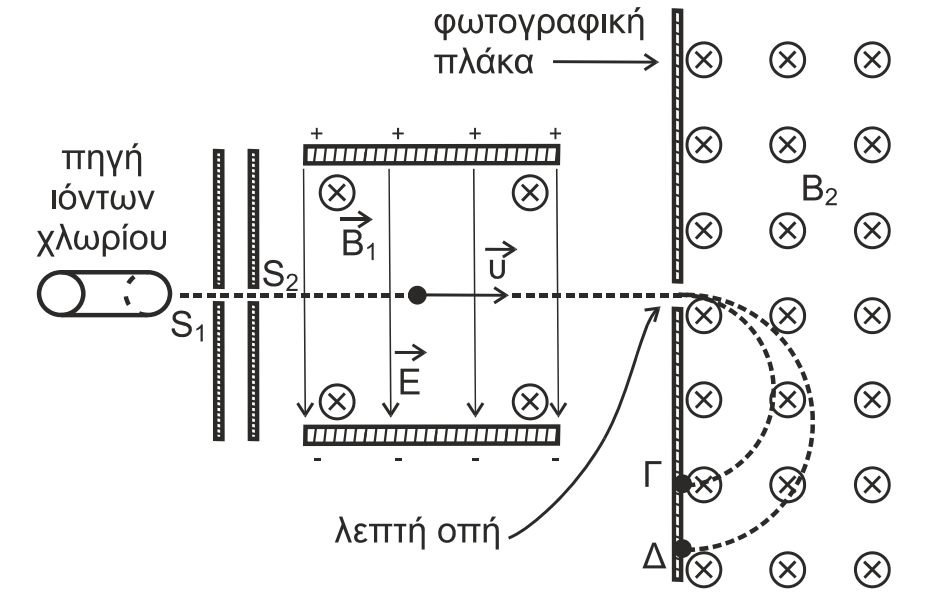
Tα ιόντα \(Cl^-\) δέχονται μαγνητική δύναμη \(F_{μαγν}\) από το μαγνητικό πεδίο και ηλεκτρική δύναμη \(F_{ηλ}\) από το ηλεκτρικό πεδίο.
\[F_{μαγν} = Β_1 \cdot |q_{Cl^-}| \cdot υ = Β_1 \cdot e \cdot υ \quad F_{ηλ} = |q_{Cl^-}| \cdot E = e \cdot E\]Για μερικά από τα ιόντα \(Cl^-\) ισχύει
\[F_{μαγν} = F_{ηλ}\]Για αυτά τα ιόντα επειδή \(ΣF=0\) η ταχύτητά τους παραμένει σταθερή και δεν εκτρέπονται κατά την κίνησή τους μέσα στον επιλογέα.
Γ2-\((6)\)
Η ταχύτητα υπολογίζεται από τη σχέση
\[Β_1 \cdot e \cdot υ=e \cdot E \Rightarrow υ= \frac{E}{B_1} \Rightarrow υ = 5 \cdot 10^4 \frac{m}{s}\]Γ3-\((6)\)
Η μόνη δύναμη που ασκείται σε κάθε ιόν που διέρχεται από τη λεπτή οπή του διαφράγματος είναι η μαγνητική δύναμη και παίζει το ρόλο της κεντρομόλου δύναμης. Οπότε αυτά τα ιόντα εκτελούν ομαλή κυκλική κίνηση.
\[F_{κεντρ} = F_{μαγν} \Rightarrow \frac{mυ^2}{R} = B_2 \cdot e \cdot υ \Rightarrow R = \frac{mυ}{eB_2}\]Επειδή ισχύει \(m_1>m_2\) θα ισχύει \(R_1>R_2\). Άρα το \(m_1\) δημιουργεί στίγμα στο σημείο \(Δ\) και το \(m_2\) στο σημείο \(Γ\).
Γ4-\((8)\)
Έστω \(Α\) το σημείο εισόδου στο ομογενές μαγνητικό πεδίο (λεπτή οπή)
\[(ΑΔ)=2R_1 = 2 \cdot \frac{m_1υ}{eB_2} \Rightarrow m_1 \frac{R_1 \cdot e \cdot B_2}{υ}\] \[(ΑΓ)=2R_2 = 2 \cdot \frac{m_2υ}{eB_2} \Rightarrow m_2 \frac{R_2 \cdot e \cdot B_2}{υ}\] \[m_1 - m_2 = \frac{(R_1 - R_2)eB_2}{υ}\]όμως για την απόσταση \(ΓΔ\) ισχύει
\[(ΓΔ) = (ΑΔ) - (ΑΓ) \Rightarrow 0,02 = 2R_1 - 2R_2 \Rightarrow R_1 - R_2 = 0,01 m\]οπότε για τη διαφορά των μαζών
\[m_1 - m_2 = \frac{0,01 \cdot 1,6 \cdot 10^{-19} \cdot 0,1}{5 \cdot 10^4} \Rightarrow m_1 - m_2 = \frac{1,6}{5} \cdot 10^{-26} kg\]με δεδομένη τη μάζα του νετρονίου \(m_n = 1,6 \cdot 10^{-27} kg\)
\[\frac{m_1 - m_2}{m_n} = \frac{\frac{1,6}{5} \cdot 10^{-26}}{1,6 \cdot 10^{-27}} \Rightarrow \frac{m_1 - m_2}{m_n} = 2\] \[m_1 - m_2 = 2 \cdot m_n\]Άρα το ισότοπο του χλωρίου μάζας \(m_1\) έχει δύο νετρόνια περισσότερα από το ισότοπο μάζας \(m_2\).
Θέμα Δ
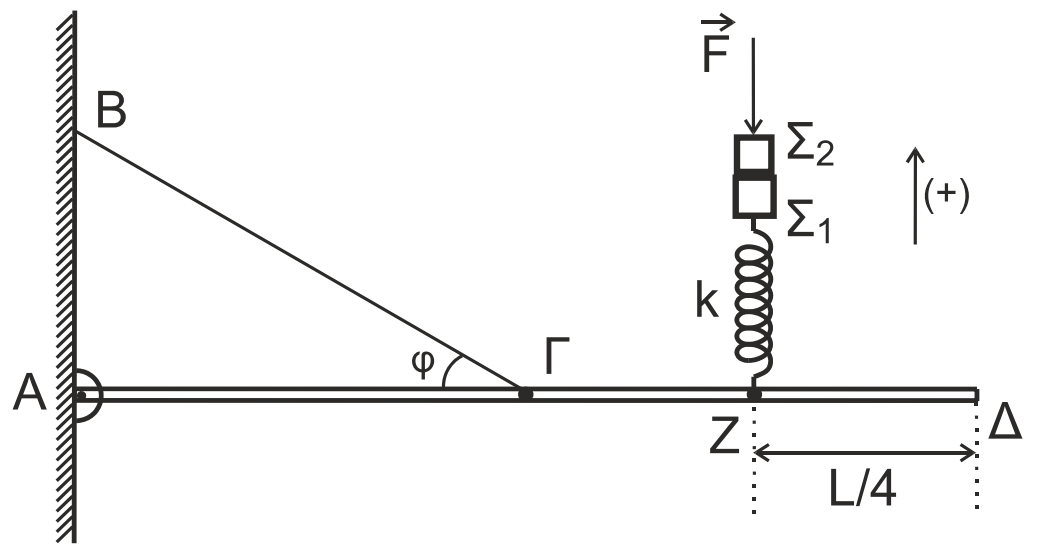
Δ1-\((4)\)
Για το σύστημα των σωμάτων \(Σ_1\) και \(Σ_2\) που ισορροπεί ισχύει
\[ΣF=0 \Rightarrow F_{ελ} - W_{ολ} - F =0 \Rightarrow k \cdot Δl -(m_1+m_2) \cdot g -F =0 \Rightarrow F=20N\]Δ2-\((6)\)
Στη θέση ισορροπίας της Α.Α.Τ. του συστήματος των σωμάτων \(Σ_1\) και \(Σ_2\)
\[ΣF=0 \Rightarrow F_{ελ} - W_{ολ} =0 \Rightarrow k \cdot Δl_0 -(m_1+m_2) \cdot g =0 \Rightarrow Δl_0 =0,1 m\]Άρα το πλάτος ταλάντωσης είναι \(Α=Δl-Δl_0 \Rightarrow A=0,2 m\)
\[D=k=(m_1+m_2)ω^2 \Rightarrow ω=\sqrt{\frac{k}{m_1+m_2}} \Rightarrow ω=10 \frac{rad}{s}\]Για την Α.Α.Τ. του σώματος \(Σ_2\)
\[D_2 = m_2 \cdot ω^2 \Rightarrow D_2=40 \frac{N}{m}\] \[ΣF=N-W_2 \Rightarrow -D_2 \cdot x=N-W_2 \Rightarrow N=4-40\cdot x, \quad (S.I.)\]Για να είναι σε επαφή τα δύο σώματα θα πρέπει \(Ν>0\)
\[4-40x>0 \Rightarrow x<0,1m \Rightarrow -0,2m \le x <0,1m\]Για \(x=0,1m=Δl_0\) δηλαδή στη θέση φυσικού μήκους του ελατηρίου χάνεται η επαφή.
Δ3-\((6)\)
Την χρονική στιγμή \(t_1\) το ελατήριο έχει το φυσικό του μήκος, άρα \(F_{ελ}=0\), οπότε το ελατήριο δεν ασκεί δύναμη στη ράβδο. Άρα για την ισορροπία της ράβου ισχύει:
\[Στ_{(Α)}=0 \Rightarrow -W_ρ \cdot \frac{L}{2} +T \cdot ημφ \cdot \frac{L}{2}=0 \Rightarrow T=80N\]Δ4-\((4)\)
Την χρονική στιγμή \(t_1\) το σώμα \(Σ_2\) αποσπάται από το σώμα \(Σ_1\) στη θέση φυσικού μήκους (Λ) του ελατηρίου έχοντας ταχύτητα \(υ_1\). Από την αρχή διατήρησης της ενέργειας ταλάντωσης έχουμε:
\[Ε=Κ_{(Λ)} + U_{(Λ)} \Rightarrow \frac{1}{2}D\cdot A^2 = \frac{1}{2}(m_1+m_2)\cdot υ_{(Λ)}^2+\frac{1}{2}D\cdot(ΟΛ)^2\]και κάνοντας τις πράξεις έχουμε \(υ_{(Λ)}=\sqrt3 \frac{m}{s}\)
To Θεώρημα μεταβολής της κινητικής ενέργεια για το σώμα \(Σ_2\)
\[K_{τελ}- Κ_{αρχ} = W_{W_2} \Rightarrow -\frac{1}{2}m_2 \cdot υ_Λ^2=-m_2 \cdot g \cdot h \Rightarrow h=0,15m\]Δ5-\((5)\)
Μετά την απομάκρυνση του \(Σ_2\) το σώμα \(Σ_1\) εκτελεί Α.Α.Τ. με
\[D=k=m_1 \cdot ω^2\]Για τη θέση ισορροπίας ισχύει
\[ΣF=0 \Rightarrow F_{ελ}-W_1=0 \Rightarrow k\cdot Δl_1 = m_1 \cdot g \Rightarrow Δl_1 = 0,06m\]και από την ΑΔΕΤ υπολογίζουμε την ενέργεια ταλάντωσης του σώματος \(Σ_1\)
\[Ε=Κ_Λ + U_Λ = \frac{1}{2} m_1 \cdot υ_Λ^2 +\frac{1}{2}D\cdot (Ο'Λ)^2 \Rightarrow E=1,08J\]Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
Ο κώδικας σε Mathematica για τη δημιουργία της γραφικής παράστασης στο θέμα \(B_1\)
A = Symbol["A"];
λ = Symbol["λ"];
f[t_] := Piecewise[ { {0, 0<=t<5}, {π/5*Cos[π*t - 5 π], 5<=t<=8} }]
Plot[f[t], {t, 0, 8},
PlotRange -> {All, {-π/4, π/4}},
AxesLabel -> {"t(s)", Subscript[υ, Δ]},
Ticks -> {Automatic, Table[{k Pi/5, Row[{k, "π/5"}]}, {k, -4, 4}]},
TicksStyle -> Directive[FontSize -> 14]]
blog comments powered by Disqus