Προσομοίωση 2020 - Β' Φάση με την νέα ύλη
ΘΕΜΑ A
Στις ερωτήσεις \(Α_1-Α_4\) να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την
ημιτελή πρόταση.
\(A_1\) Ένα σώμα εκτελεί ταυτόχρονα δύο απλές αρμονικές ταλαντώσεις με ίδιο πλάτος \(Α\), ίδιας διεύθυνσης, γύρω από το ίδιο σημείο, με συχνότητες \(f_1\) και \(f_2\), που διαφέρουν λίγο μεταξύ τους. Τότε:
α. Η περιοδική κίνηση του σώματος έχει σταθερό πλάτος \(\mid{Α΄}\mid = 2A\)
β. Το σώμα εκτελεί απλή αρμονική ταλάντωση
γ. Η συχνότητα της περιοδικής κίνησης του σώματος είναι \(\mid{f_1} - f_2\mid\)
δ. Η περίοδος της περιοδικής κίνησης του σώματος είναι \(\frac{2}{f_1+f_2}\)
Μονάδες 5
\(A_2\)
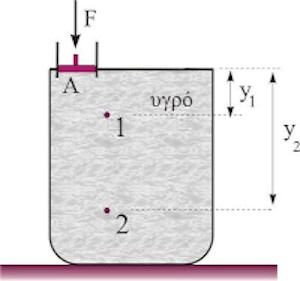
Το κλειστό δοχείο του σχήματος βρίσκεται στην επιφάνεια της Γης και περιέχει υγρό πυκνότητας \(ρ\). Στο έμβολο εμβαδού \(Α\) ασκείται κατακόρυφη δύναμη μέτρου \(F\). Αν \(p_1\), \(p_2\) οι πιέσεις στα σημεία \(1\) και \(2\) αντίστοιχα, ισχύει:
- $$ p_2 - p_1 = ρ \cdot g \cdot (y_2 – y_1) $$
- $$ p_1 = p_2 = p_{ατμ} + \frac{F}{A} $$
- $$ p_1 = p_2 = \frac{F}{A} $$
- $$ p_2 – p_1 = \frac{F}{A} +ρ \cdot g \cdot (y_2 - y_1) $$
Μονάδες 5
\(A_3\)
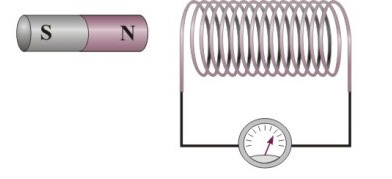
Στο σχήμα, μεγαλύτερη ηλεκτρεγερτική δύναμη από επαγωγή αναπτύσσεται στο πηνίο όταν ο μαγνήτης:
α. βρίσκεται ακίνητος ολόκληρος μέσα στο πηνίο
β. πλησιάζει αργά το πηνίο
γ. είναι ακίνητος μπροστά από το πηνίο
δ. απομακρύνεται γρήγορα από το πηνίο
Μονάδες 5
\(A_4\)
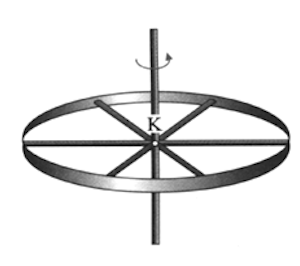
Ένας τροχός ακτίνας \(R\) εκτελεί στροφική κίνηση γύρω από άξονα που διέρχεται από το κέντρο του \(Κ\), ξεκινώντας από την ηρεμία και επιταχύνεται με γωνιακή επιτάχυνση που συνεχώς αυξάνεται. Τότε:
α. η γραμμική ταχύτητα \(υ\) ενός οποιουδήποτε σημείου του τροχού αυξάνεται γραμμικά με τον χρόνο
β. η γωνιακή ταχύτητα \(ω\) του τροχού δίνεται από την σχέση \(ω = α_{γων} \cdot t\)
γ. η στιγμιαία γραμμική ταχύτητα \(υ\) ενός σημείου της περιφέρειας του τροχού συνδέεται με την στιγμιαία γωνιακή του ταχύτητα \(ω\) με την σχέση \(υ = ω \cdot R\)
δ. η γωνία που διαγράφει ο τροχός σε χρόνο \(Δt\) υπολογίζεται από την σχέση \(Δθ = \frac{1}{2} \cdot α_{γ} \cdot Δt^2\)
Μονάδες 5
\(A_5\)
Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
α. Η περίοδος μιας φθίνουσας ταλάντωσης παραμένει σταθερή για ορισμένη τιμή της σταθεράς απόσβεσης \(b\).
β. Σώμα εκτελεί απλή αρμονική ταλάντωση. Στις θέσεις όπου ο ρυθμός μεταβολής της ορμής του είναι ίσος με μηδέν, το μέτρο της ταχύτητάς του είναι μηδέν.
γ. Η υδροστατική πίεση σε ένα σημείο ενός υγρού που περιέχεται σε ένα δοχείο είναι ανάλογη της απόστασης από τον πυθμένα του δοχείου.
δ. Όταν σε ελεύθερο, αρχικά ακίνητο στερεό, ασκείται ροπή ζεύγους το στερεό εκτελεί μόνο στροφική κίνηση.
ε. Οι μαγνητικές δυναμικές γραμμές του πεδίου που δημιουργεί ένας ευθύγραμμος ρευματοφόρος αγωγός μεγάλου μήκους είναι ομόκεντροι κύκλοι με κέντρο πάνω στον αγωγό.
Μονάδες 5
ΘΕΜΑ Β
\(Β_1\)
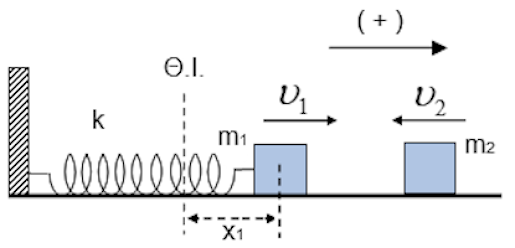
Σώμα \(Σ_1\), μάζας \(m_1 = 3 \cdot m\), είναι δεμένο στο ελεύθερο άκρο οριζόντιου ελατηρίου και εκτελεί απλή αρμονική ταλάντωση με περίοδο \(Τ\), πλάτος \(Α\) και ενέργεια \(Ε\). Κάποια στιγμή που το σώμα διέρχεται από τη θέση \(x_1 = + \frac{A}{2}\), με \(υ_1 > 0\), συγκρούεται μετωπικά και ελαστικά με σώμα \(Σ_2\) μάζας \(m_2 = m\), που κινείται με ταχύτητα \(\vec{υ_2}\) αντίθετης φοράς της \(\vec{υ_1}\) . Το σώμα \(Σ_1\) μετά την κρούση εκτελεί ταλάντωση με ενέργεια \(Ε΄ = \frac{Ε}{4}\). Ο λόγος των μέτρων των ταχυτήτων \((\frac{υ_1}{υ_2})\) των δύο σωμάτων, ελάχιστα πριν συγκρουστούν, ισούται με:
- $$ 1 $$
- $$ 2 $$
- $$ \frac{1}{2} $$
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση
Μονάδες 2
Να αιτιολογήσετε την απάντησή σας
Μονάδες 7
\(Β_2\)
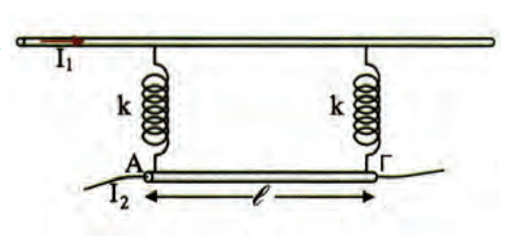
Μία ακλόνητη οριζόντια μεταλλική ράβδος έχει μεγάλο μήκος και διαρρέεται από ρεύμα \(I_1\). Από τη ράβδο μέσω δύο ελατηρίων κρέμεται μια άλλη ράβδος \(ΑΓ\) μήκους \(l\). Όταν η ράβδος \(ΑΓ\) διαρρέεται από ρεύμα \(I_2\) ομόρροπο με το ρεύμα της πρώτης ράβδου, τα ελατήρια βρίσκονται στο φυσικό τους μήκος \(l_o\). Όταν αντιστραφεί η φορά του ρεύματος σε μία από τις δύο ράβδους τα ελατήρια επιμηκύνονται και το σύστημα ισορροπεί όταν η απόσταση μεταξύ των ράβδων γίνει \(d = \frac{5 \cdot l_o}{4}\). Η σταθερά k των ελατηρίων ισούται με:
- $$k = \frac{18 \cdot m \cdot g}{5 \cdot l_o}$$
- $$ k = \frac{18 \cdot m \cdot g}{25 \cdot l_o} $$
- $$ k = \frac{4 \cdot m \cdot g}{l_o} $$
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση
Μονάδες 2
Να αιτιολογήσετε την απάντησή σας
Μονάδες 6
\(Β_3\)
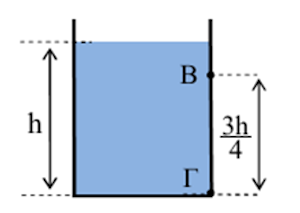
H κυλινδρική δεξαμενή που φαίνεται στο διπλανό σχήμα είναι γεμάτη με υγρό μέχρι το ύψος \(h\) και έχει στα σημεία \(Β\) και \(Γ\) του πλευρικού τοιχώματος δύο μικρές τρύπες ίδιου εμβαδού \(Α\). Το σημείο \(Β\) απέχει απόσταση \(\frac{3h}{4}\) από το έδαφος του σχήματος ενώ το σημείο \(Γ\) είναι πολύ κοντά στον πυθμένα του δοχείου. Η δεξαμενή τροφοδοτείται από μια βρύση σταθερής παροχής \(Π\). Για να παραμένει η στάθμη του νερού μέσα στη δεξαμενή σταθερή στο ύψος \(h\), η παροχή \(Π\) θα πρέπει να είναι ίση με :
- $$ 3Α \sqrt{2gh} $$
- $$ \frac{Α}{2} \sqrt{2gh} $$
- $$ \frac{3Α}{2} \sqrt{2gh} $$
Να επιλέξετε το γράμμα που αντιστοιχεί στη σωστή απάντηση
Μονάδες 2
Να αιτιολογήσετε την απάντησή σας
Μονάδες 6
ΘΕΜΑ Γ
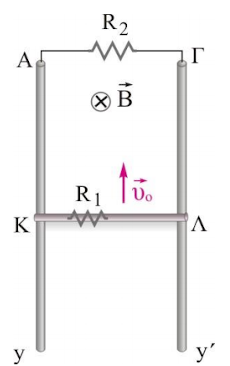
Στη παραπάνω διάταξη, ο αγωγός \(ΚΛ\) έχει αντίσταση \(R_1=0.5Ω\), μήκος \(l=1m\), μάζα \(m=0.3kg\) και αποτελεί τμήμα ενός κλειστού κυκλώματος που δημιουργούν οι κατακόρυφοι παράλληλοι αγωγοί-οδηγοί \(Αy, \quad Γy΄\) και ο αντιστάτης \(R_2=1.5Ω\). Ο αγωγός ΚΛ μπορεί να κινείται χωρίς τριβή, πάνω στους αγωγούς \(Αy, \quad Γy'\), που είναι αμελητέας αντίστασης, παραμένοντας διαρκώς κάθετος σε αυτούς. Η όλη διάταξη βρίσκεται μέσα σε οριζόντιο ομογενές μαγνητικό πεδίο έντασης μέτρου \(Β=1Τ\), του οποίου οι δυναμικές γραμμές είναι κάθετες στο επίπεδο που ορίζουν οι αγωγοί \(Αy, \quad Γy΄\) και έχουν φορά από τον αναγνώστη προς τη σελίδα.
Τον αρχικά ακίνητο αγωγό \(ΚΛ\), τη χρονική στιγμή \(t_ο=0s\) τον εκτοξεύουμε προς τα πάνω με αρχική ταχύτητα \(3 \frac{m}{s}\). Η θερμική ενέργεια που εκλύεται στους ωμικούς αντιστάτες λόγω φαινομένου \(Joule\) μέχρι την στιγμή που ο αγωγός σταματά στιγμιαία είναι \(0.6J\).
\(Γ_1\) Αμέσως μετά την εκτόξευση του αγωγού \(ΚΛ\), να προσδιορίσετε την φορά και την ένταση του επαγωγικού ρεύματος που θα δημιουργηθεί στο κύκλωμα.
Μονάδες 6
\(Γ_2\) Να βρείτε την επιτάχυνση του αγωγού \(ΚΛ\) τη χρονική στιγμή \(t_o=0\).
Μονάδες 6
\(Γ_3\) Να βρείτε πόσο μετατοπίστηκε ο αγωγός \(ΚΛ\) μέχρι να σταματήσει στιγμιαία.
Μονάδες 6
\(Γ_4\) Να βρείτε το ρυθμό μεταβολής της κινητικής ενέργειας του αγωγού \(ΚΛ\) την χρονική στιγμή για την οποία ισχύει \(υ = \frac{υ_{ορ}}{2}\), όπου \(υ_{ορ}\) η οριακή ταχύτητα που αποκτά τελικά η ράβδος κατά την κάθοδό της.
Μονάδες 7
Δίνεται η επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\)
ΘΕΜΑ Δ
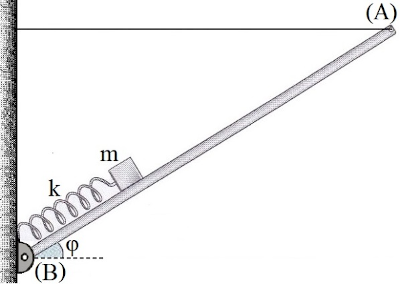
Μια ομογενής, λεπτή και λεία ράβδος \(ΑΒ\) έχει μήκος \(L = 4m\) και μάζα \(M = 10kg\). Το άκρο \(Β\) της ράβδου συνδέεται με άρθρωση σε κατακόρυφο τοίχο, ενώ το άλλο της άκρο \(Α\) συνδέεται με τον τοίχο με τη βοήθεια οριζόντιου αβαρούς και μη εκτατού νήματος, που έχει όριο θραύσης \(T_{θρ} = 51Ν\). Στο άκρο \(Β\) της ράβδου είναι στερεωμένο το ένα άκρο ιδανικού ελατηρίου σταθεράς \(k = 64 \frac{N}{m}\) και φυσικού μήκους \(l_o = 1.5m\). Στο άλλο άκρο του ελατηρίου είναι δεμένο σώμα \(Σ\) μάζας \(m = 4kg\) αμελητέων διαστάσεων. Το σύστημα ελατηρίου – σώματος ισορροπεί αρχικά πάνω στη ράβδο και η ράβδος ισορροπεί, σχηματίζοντας με τον ορίζοντα γωνία \(φ\) \((ημφ = 0.8 \quad συνφ = 0.6)\). Η επιτάχυνση της βαρύτητας είναι \(g = 10 \frac{m}{s^2}\).
\(Δ_1\) Στην αρχική κατάσταση ισορροπίας, να υπολογίσετε το μέτρο της τάσης του νήματος που δέχεται το άκρο \(Α\) της ράβδου.
Μονάδες 6
Τη χρονική στιγμή \(t = 0\) εκτοξεύουμε το σώμα \(Σ\) με ταχύτητα μέτρου \(υ_1 = 2 \frac{m}{s}\), παράλληλα στη ράβδο με φορά προς τα πάνω, οπότε το σώμα αρχίζει να εκτελεί α.α.τ. χωρίς το νήμα να σπάσει.
\(Δ_2\) Να υπολογίσετε την ελάχιστη απόσταση από το άκρο \(Α\), στην οποία θα φτάσει το σώμα \(Σ\) κατά τη διάρκεια της ταλάντωσής του.
Μονάδες 4
\(Δ_3\) Θεωρώντας ως θετική τη φορά της ταχύτητας εκτόξευσης, να γράψετε τη χρονική εξίσωση της τάσης του νήματος που δέχεται η ράβδος.
Μονάδες 8
\(Δ_4\) Να υπολογίσετε τη μέγιστη τιμή του μέτρου της ταχύτητας, με την οποία πρέπει να εκτοξεύσουμε το σώμα \(Σ\), παράλληλα στη ράβδο, ώστε κατά τη διάρκεια της ταλάντωσής του το νήμα να μην σπάσει.
Μονάδες 7
blog comments powered by Disqus