Μοριοδότηση 2020
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(α\)
Α3 - \(γ\)
Α4 - \(δ\)
Α5: \(Σ - Λ - Σ - Σ - Λ\)
Θέμα Β
B1-\((iii)-2-6\)
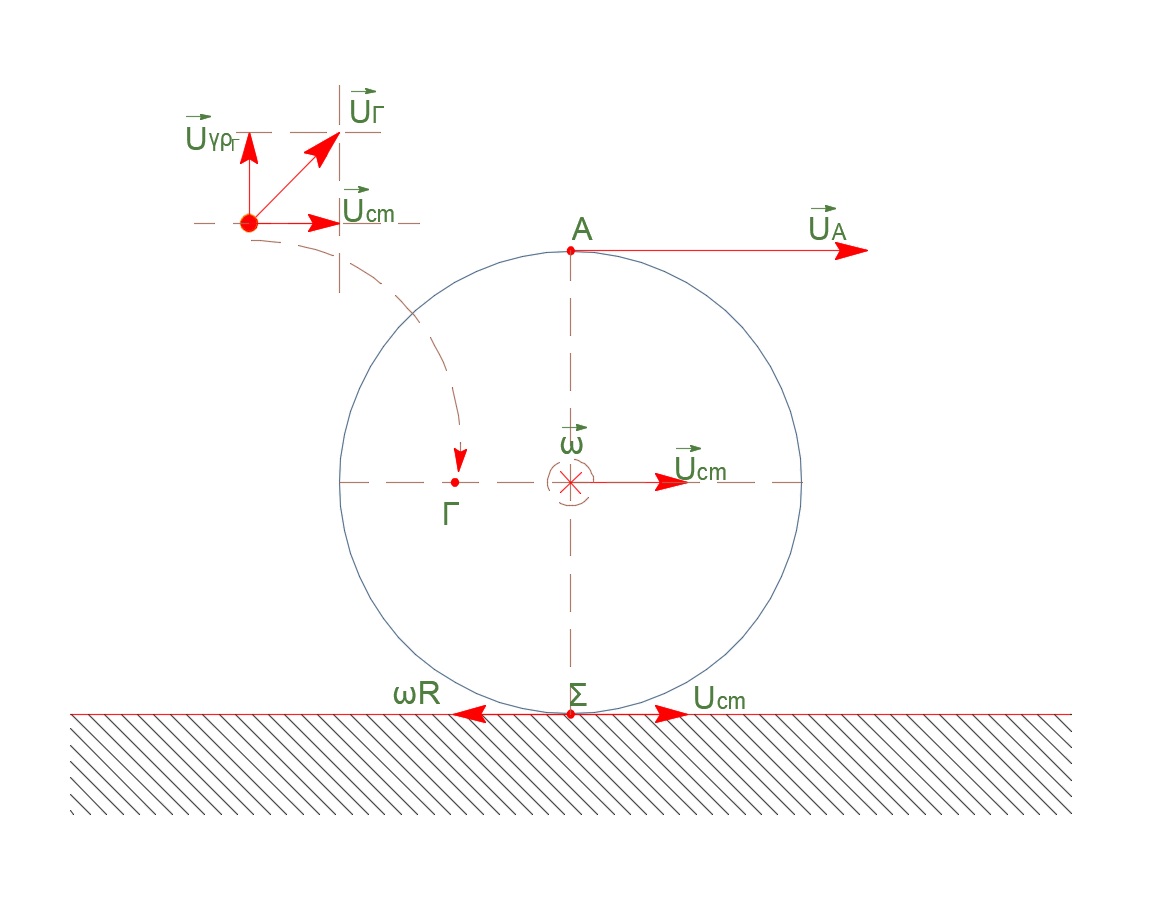
Έστω \(Σ\) το σημείο επαφής του τροχού με το οριζόντιο επίπεδο. Το σημείο \(Σ\) περιστρέφεται γύρω από το σημείο \(Ο\) με γωνιακή ταχύτητα \(ω\) και το \(Ο\) περιστρέφεται γύρω από το σημείο \(Σ\) με την ίδια γωνιακή ταχύτητα. Δηλαδή θεωρούμε το σημείο \(Σ\) ως στιγμιαίο άξονα περιστροφής. Μπορούμε δηλαδή να θεωρήσουμε ότι για μικρή χρονική διάρκεια το σημείο \(Σ\) παραμένει ακίνητο και γύρω από αυτό περιστρέφεται ο τροχός, χωρίς να μεταφέρεται, αφού η στιγμιαία ταχύτητα του άξονα είναι μηδενική. Αυτό σημαίνει ότι ο τροχός δεν κάνει σύνθετη κίνηση αλλά για μικρή χρονική διάρκεια έχουμε μια στροφική κίνηση γύρω από νοητό άξονα που διέρχεται από το σημείο \(Σ\).
\[υ_Α = ω \cdot (ΣΑ) = ω \cdot 2 \cdot R\] \[υ_Γ = ω \cdot (ΣΓ) = ω \cdot \sqrt{(ΣΟ)^2+(ΟΓ)^2} = ω \cdot \sqrt{R^2+ \frac{R^2}{4}} = ω \cdot R \frac{\sqrt{5}}{2}\] \[\frac{υ_Γ}{υ_Α} = \frac{\sqrt5}{4}\]άρα σωστό το \(iii\)
Β2 - \((ii)-2-6\)
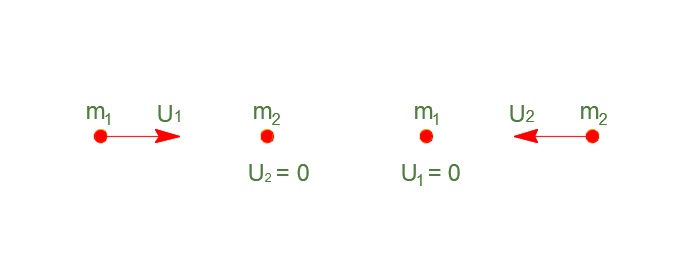
Ομοίως
\[υ_1' = \frac{2\cdot m_2}{m_1 + m_2} \cdot υ_2\] \[Π_2(\%) = \frac{K_1'}{K_2} \cdot 100 \% \Rightarrow Π_2(\%) = \frac{4 \cdot m_1 \cdot m_2}{(m_1+m_2)^2} \cdot 100 \%\]Άρα \(Π_1(\%) = Π_2(\%)\)
άρα σωστό το \(ii\)
Β3 - \((i)-2-7\)
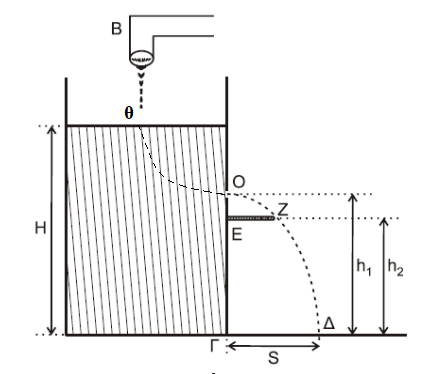
\(Π_Β = Π_Ο\) διότι \(H=σταθ.\)
Εξίσωση Bernoulli (Θ –> Ο)
\[P_Θ + \frac{1}{2} \cdot ρ \cdot υ_Θ^2 + ρ \cdot g \cdot (H -h_1) = P_O + \frac{1}{2} \cdot ρ \cdot υ_O^2+ 0\] \[P_Θ = P_O = P_{ατμ} \quad υ_Θ = 0 \quad \Rightarrow υ_Ο = \sqrt{2 \cdot g \cdot (H - h_1)}\] \[α) \underline {τρόπος}\](O –> Δ:)
\[άξονας \quad x \quad s = υ_Ο \cdot t \Rightarrow t = \frac{s}{υ_Ο}\] \[άξονας \quad y \quad h_1 = \frac{1}{2} \cdot g \cdot t^2 \Rightarrow h_1 = \frac{g \cdot s^2}{2\cdot υ_Ο^2}\](O –> Ζ:)
\[άξονας \quad x \quad \frac{s}{2} = υ_Ο \cdot t' \Rightarrow t' = \frac{s}{2 \cdot υ_Ο}\] \[άξονας \quad y \quad h_1 - h_2 = \frac{1}{2} \cdot g \cdot t'^2 \Rightarrow h_1 - h_2 = \frac{g \cdot s^2}{8\cdot υ_Ο^2}\] \[h_1 - h_2 = \frac{h_1}{4} \Rightarrow h_2 = \frac{3 \cdot h_1}{4} \Rightarrow h_1 = \frac{7}{8} \cdot H\] \[Π_Ο = Α \cdot υ_Ο \Rightarrow Π_Β = Α \cdot \sqrt{2 \cdot g \cdot \frac{H}{8}} \Rightarrow Π_Β = \frac{A}{2} \cdot \sqrt{g\cdot H}\]άρα σωστό το \(i\)
\[β) \underline {τρόπος}\] \[υ_Ο = \sqrt{2 \cdot g \cdot (H - h_1)} \Rightarrow Π = Α \cdot \sqrt{2 \cdot g \cdot (H - h_1)}\]Αν η παροχή της βρύσης είναι \(Π = \frac{A}{2} \cdot \sqrt{g \cdot H}\)
τότε εξισώνοντας τις παροχές έχουμε:
\[Α \cdot \sqrt{2 \cdot g \cdot (H - h_1)} = \frac{A}{2} \cdot \sqrt{g \cdot H} \Rightarrow 2 \cdot g \cdot (H-h_1) = \frac{g \cdot H}{4}\]και κάνοντας τις πράξεις:
\[h_1 = \frac{7 \cdot H}{8}\]Αν η παροχή της βρύσης είναι \(Π = 2Α \cdot \sqrt{g \cdot H}\)
τότε εξισώνοντας τις παροχές έχουμε:
\[Α \cdot \sqrt{2 \cdot g \cdot (H - h_1)} = 2Α \cdot \sqrt{g \cdot H} \Rightarrow 2 \cdot g \cdot (H-h_1) = 4 \cdot g \cdot H\]και κάνοντας τις πράξεις οδηγούμαστε σε άτοπο αφού:
\[h_1 = -H\]Αν η παροχή της βρύσης είναι \(Π = A \cdot \sqrt{2 \cdot g \cdot H}\)
τότε εξισώνοντας τις παροχές έχουμε:
\[Α \cdot \sqrt{2 \cdot g \cdot (H - h_1)} = A \cdot \sqrt{2 \cdot g \cdot H} \Rightarrow 2 \cdot g \cdot (H-h_1) = 2 \cdot g \cdot H\]και κάνοντας τις πράξεις οδηγούμαστε πάλι σε άτοπο αφού:
\[h_1 = 0\]άρα σωστό το \(i\)
\[γ) \underline {τρόπος - λάθος}\]Γνωρίζουμε ότι η παροχή της βρύσης είναι ίση με την παροχή της οπής \(Ο\) αφού το ύψος \(Η\) παραμένει σταθερό.
Με δεδομένο ότι η παροχή δίνεται από την σχέση \(Π = Α \cdot υ\) οι πιθανές ταχύτητες εκροής του νερού είναι
\[\frac{\sqrt{g \cdot H}}{2} = \sqrt{\frac{g \cdot H}{4}} = \sqrt{2 \cdot g \cdot \frac{H}{8} }\] \[2 \cdot \sqrt{g \cdot H} = \sqrt{4 \cdot g \cdot H} = \sqrt{2 \cdot g \cdot 2H}\] \[\sqrt{2 \cdot g \cdot H}\]Σύμφωνα με το θεώρημα Τορικέλι η ταχύτητα εκροής νερού από το στόμιο \(Ο\) που βρίσκεται σε βάθος \(h\) από την ελεύθερη επιφάνειά του είναι ίση με την ταχύτητα που θα είχε το υγρό αν έπεφτε ελεύθερα από ύψος \(h\).
Από το θεώρημα Τορικέλι απορρίπτεται η δεύτερη λύση αφού τέτοια ταχύτητα εκροής προκύπτει για βάθος \(2 \cdot H\). Παρόμοια απορρίπτεται και η τρίτη λύση αφού τέτοια ταχύτητα εκροής προκύπτει για βάθος \(Η\).
άρα σωστό το \(i\)
Θέμα Γ
Γ1-\((6)\)
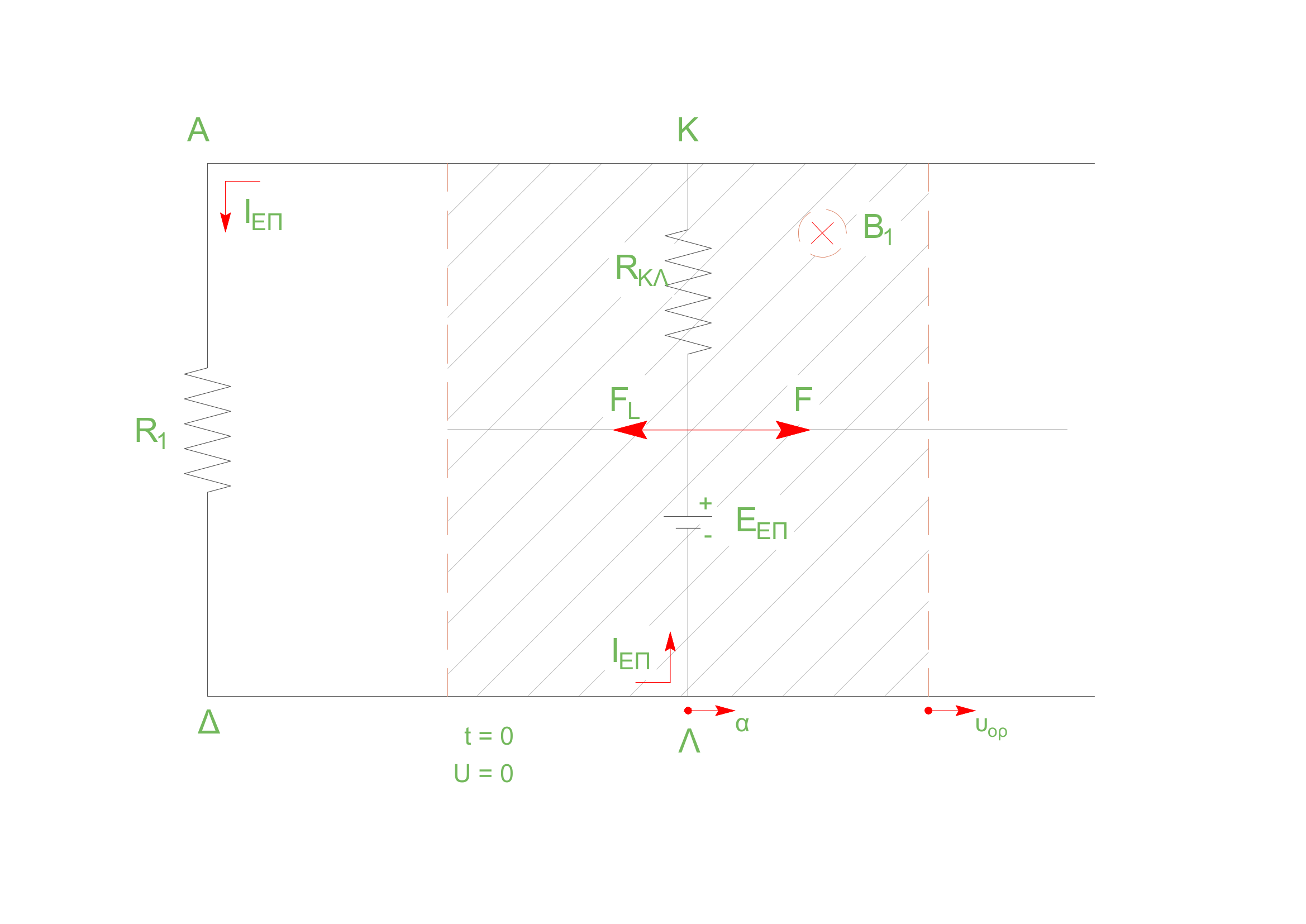
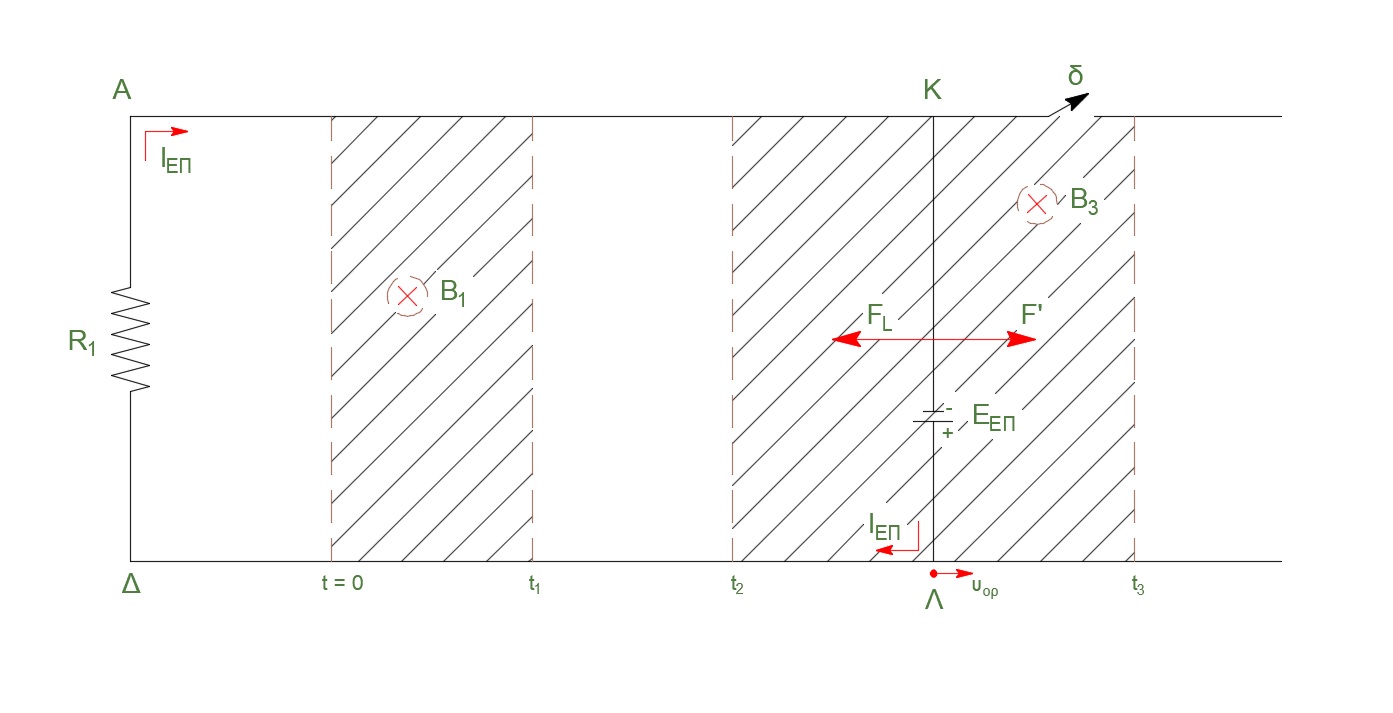
Αφού η μαγνητική ροή που διέρχεται από το κύκλωμα \(ΑΚΛΔΑ\) αυξάνεται, το επαγωγικό ρεύμα δημιουργεί δικό του μαγνητικό πεδίο που έχει σύμφωνα με τον κανόνα του \(Lenz\) αντίθετη φορά από αυτό που ήδη υπάρχει (δηλαδή δημιουργεί μαγνητικό πεδίο με φορά από την σελίδα προς τον αναγνώστη). Για να συμβαίνει αυτό, πρέπει, σύμφωνα με τον κανόνα του δεξιού χεριού, το επαγωγικό ρεύμα να έχει φορά αντίθετη από αυτήν της φοράς κίνησης των δεικτών του ρολογιού. Η επαγωγική τάση φαίνεται στο σχήμα.
\[β) \underline {τρόπος}\]Σύμφωνα με τον κανόνα του \(Lenz\), η φορά του επαγωγικού ρεύματος είναι τέτοια, ώστε να αντιστέκεται στην αιτία που το προκαλεί. Η αιτία που προκαλεί την αύξηση της μαγνητικής ροής είναι η κίνηση της ράβδου με φορά προς τα δεξιά υπό την επίδραση της δύναμης \(F\). Συνεπώς το επαγωγικό ρεύμα έχει φορά τέτοια (σύμφωνα με τον κανόνα του δεξιού χεριού φορά προς τα αριστερά), ώστε η δύναμη Laplace που δέχεται η ράβδος να αντιστέκεται στην κίνησή του .
\[γ) \underline {τρόπος}\]Στην ράβδο υπάρχουν ελεύθερα ηλεκτρόνια το οποία συμμετέχουν στην προς τα δεξιά κίνηση της. Αυτά τα αρνητικά φορτία κινούνται με ταχύτητα \(υ\) κάθετη στις δυναμικές γραμμές του ομογενούς μαγνητικού πεδίου. Το μαγνητικο πεδίο ασκεί δύναμη \((Lorentz)\) που είναι κάθετη στο επίπεδο που ορίζεται από την ταχύτητα και την διεύθυνση του πεδίου και η φορά της δίνεται από τον κανόνα του δεξιού χεριού. Η δύναμη αυτή προκαλεί την κίνηση των ελεύθερων ηλεκτρονίων προς το άκρο \(Λ\). Έτσι δημιουργείται συσσώρευση αρνητικού φορτίου στο άκρο \(Λ\) και πλεόνασμα θετικού φορτίου στο άκρο \(Κ\). Τα φορτία αυτά δημιουργούν στο χώρο του αγωγού ομογενές ηλεκτρικό πεδίο ένασης \(Ε\) με φορά από το \(Κ\) προς το \(Λ\). Τα ελεύθερα ηλεκτρόνια δέχονται τώρα μια δύναμη \(F_{ηλ} = E \cdot |q|\) αντίθετης φοράς από την μαγνητική. Όσο η δύναμη Lorentz είναι μεγαλύτερη από την ηλεκτρική η συσσώρευση φορτίου συνεχίζεται με όλο και μικρότερο ρυθμό. Έτσι η ένταση του ηλεκτρικού πεδίου αυξάνεται και σε πολύ λίγο χρόνο τα μέτρα των δυο δυνάμεων γίνονται ίσα.
\[Ε \cdot |q| = B \cdot υ \cdot |q| \Rightarrow E = B \cdot υ\]Τότε παύει η μετακίνηση φορτίου και το σημείο \(Κ\) βρίσκεται σε υψηλότερο δυναμικό από το \(Λ\). Η διαφορά δυναμικού μεταξύ των άκρων του αγωγού είναι
\[Ε = \frac{Ε_{επ}}{L} \Rightarrow Ε_{επ} = Ε \cdot L \Rightarrow E_{επ} = Β \cdot υ \cdot L\]Το κλειστό κύκλωμα \(ΑΚΛΔΑ\) διαρρέεται από επαγωγικό ρεύμα του οποίου η ένταση είναι
\[Ι_{επ} = \frac{E_{επ}}{R_{ολ}} \Rightarrow I_{E_{επ}} = \frac{E_{επ}}{R_1 + R_{ΚΛ}}\] \[F_L = B \cdot I_{Ε_{επ}} \cdot l \Rightarrow F_L = B^2 \cdot l^2 \cdot \frac{υ}{R_1 + R_{ΚΛ}}\] \[Σ \vec F = m \cdot \vecα \Rightarrow F - F_L = m \cdot α \Rightarrow F - B^2 \cdot l^2 \cdot \frac{υ}{R_1 + R_{ΚΛ}} = m α\]Ευθύγραμμη επιταχυνόμενη κίνηση με μειούμενη επιτάχυνση. Η ταχύτητα αυξάνεται, άρα η δύναμη Laplace αυξάνεται, άρα η συνισταμένη δύναμη μειώνεται άρα η επιτάχυνση μειώνεται. Μέχρι:
\[α = 0 \Rightarrow ΣF = 0 \Rightarrow B^2 \cdot l^2 \cdot \frac{υ_{ορ}}{R_1 + R_{ΚΛ}} = F\] \[υ_{ορ} = \frac{F \cdot (R_1 + R_{ΚΛ})}{Β^2 \cdot l^2} \Rightarrow υ_{ορ} = 4 \frac{m}{s}\]Γ2-\((6)\)
Γ3-\((6)\)
\[α) \underline {τρόπος}\] \[I'_{επ} = \frac{q_{επ}}{Δt} \Rightarrow Δt = \frac{q_{επ}}{Ι'_{επ}} \Rightarrow Δt = 0.25s\] \[\left. \begin{matrix} Q_1 = I'^2_{επ} \cdot R_1 \cdot Δt \\\\ Q_2 = I'^2_{επ} \cdot R_{ΚΛ} \cdot Δt \end{matrix} \right\} Q = Q_1 + Q_2 = 0.8 Joule\] \[β) \underline {τρόπος}\] \[q_{επ} = \frac{ΔΦ}{R_{ολ}} \Rightarrow ΔΦ = q_{επ} \cdot (R_1 + R_{ΚΛ}) \Rightarrow B_3 \cdot Δx \cdot l = q_{επ} \cdot (R_1 + R_{ΚΛ})\] \[B_3 \cdot υ_{ορ} \cdot Δt \cdot l = q_{επ} \cdot (R_1 + R_{ΚΛ}) \Rightarrow Δt = \frac{q_{επ} \cdot (R_1 + R_{ΚΛ})}{B_3 \cdot υ_{ορ} \cdot l} \Rightarrow Δt = 0.25s\] \[Q = I'^2_{επ} \cdot (R_1 + R_{ΚΛ}) \cdot Δt \Rightarrow Q = 0.8 Joule\] \[γ) \underline {τρόπος}\] \[q_{επ} = \frac{ΔΦ}{R_{ολ}} \Rightarrow ΔΦ = q_{επ} \cdot (R_1 + R_{ΚΛ}) \Rightarrow B_3 \cdot Δx \cdot l = q_{επ} \cdot (R_1 + R_{ΚΛ})\] \[Δx = \frac{q_{επ} \cdot (R_1 + R_{ΚΛ})}{B_3 \cdot l}\] \[ΘΜΚΕ_{(t_1 \rightarrow t_2)} \quad ΔΚ = ΣW\] \[K_{t_3} - Κ_{t_2} = W_F' + W_{F_L} \Rightarrow 0 = W_{F'} + W_{F_L} \Rightarrow W_{F'} = -W_{F_L} = F_L \cdot Δx\] \[W_{F_L} = B_3 \cdot I_{επ} \cdot l \cdot \frac{q_{επ} \cdot (R_1 + R_{ΚΛ})}{B_3 \cdot l} \Rightarrow W_{F'} = 0.8 Joule\] \[Q = |W_{F'}| \Rightarrow Q = 0.8 Joule\] \[δ) \underline {τρόπος}\] \[Ε_{επ} = \frac{dW_{πηγής}}{dq}\] \[Q = W_{πηγής} = Σ(dW_{πηγής}) = ΣΕ_{επ} \cdot dq = E_{επ} \cdot Σdq = E_{επ} \cdot q_{επ} = 0.8 Joule\]Γ4-\((7)\)
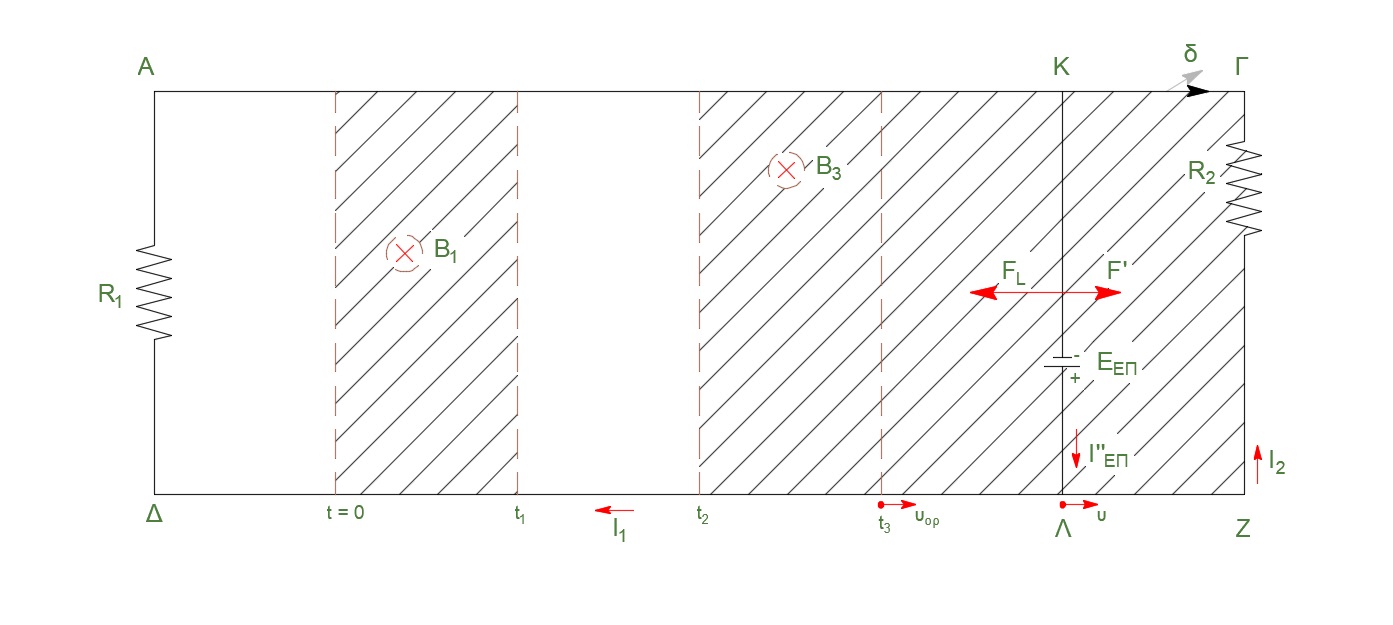
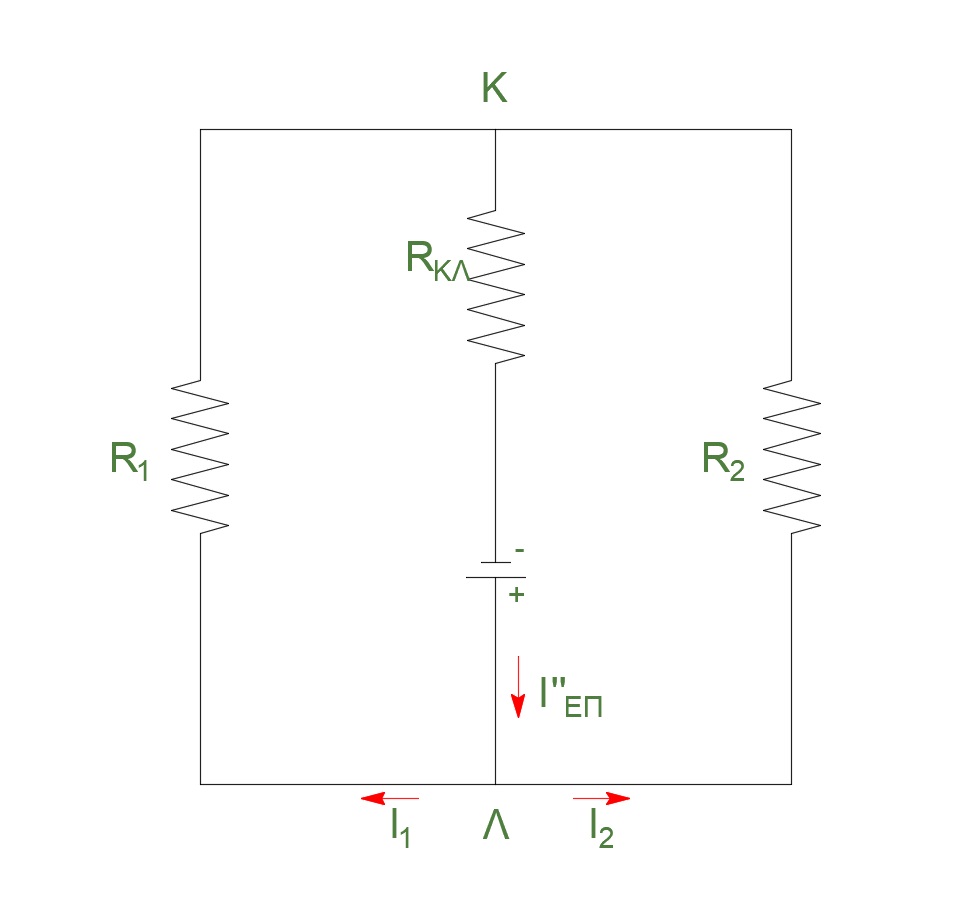
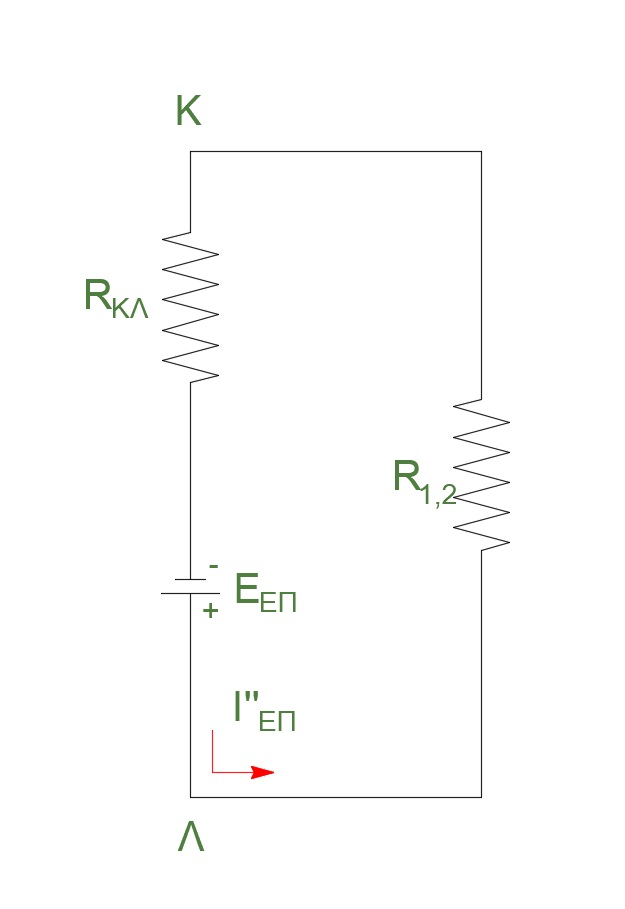
την χρονική στιγμή \(t_3^+:\)
\[υ_{ορ} = 4 \frac{m}{s} \quad F_{L3} = 1N > F' = 0.8N\]άρα η ταχύτητα μικραίνει, η δύναμη Laplace μικραίνει έως ότου
\[F' - F_L =0 \Rightarrow υ = υ'_{ορ} \Rightarrow F' = \frac{B^2_3 \cdot l^2 \cdot υ'_{ορ}}{R_{12} + R_{ΚΛ}} \Rightarrow υ'_{ορ} = 3.2 \frac{m}{s}\] \[α) \underline {τρόπος}\] \[V_{ΚΛ} = Ι''_{επ} \cdot R_{12} \ \Rightarrow V_{ΚΛ} = \frac{Ε_{επ}}{R_{ολ}} \cdot R_{12} \Rightarrow V_{ΚΛ} = \frac{B_3 \cdot l^2 \cdot υ'_{ορ}}{R_{12} + R_{ΚΛ}} \cdot R_{12}\] \[|V_{KL}| = 0.8 Volt\] \[β) \underline {τρόπος}\] \[V_{ΚΛ} = Ε_{επ} - I''_{επ} \cdot R_{ΚΛ} = Β_3 \cdot l \cdot υ_{ορ} - \frac{E_{επ}}{R_{ολ}} \cdot R_{ΚΛ} = 0.8 Volts\] \[V_{ΚΛ} = I_1 \cdot R_1 \Rightarrow I_1 = \frac{V_{ΚΛ}}{R_1} \Rightarrow I_1 = 0.4A\] \[V_{ΚΛ} = I_2 \cdot R_2 \Rightarrow I_2 = \frac{V_{ΚΛ}}{R_2} \Rightarrow I_2 = 0.4A\]Θέμα Δ
Δ1-\((6)\)
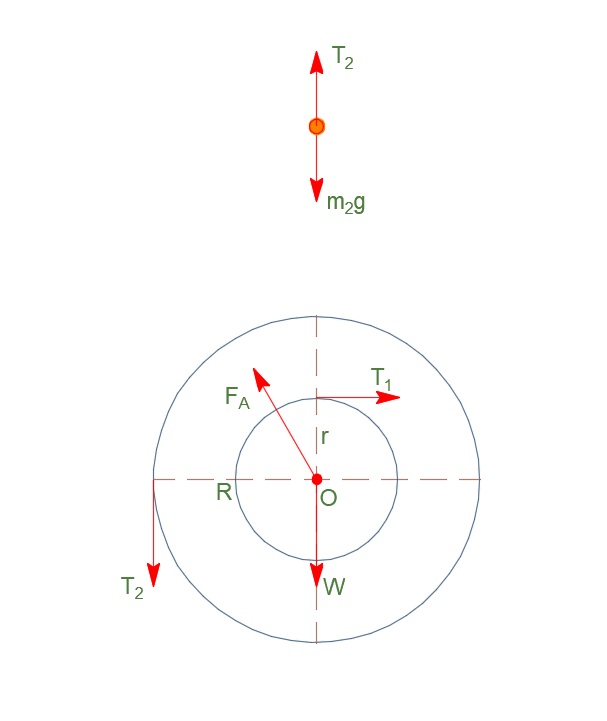
νήμα (2) αβαρές, μη εκτατό \(T'_2 = T_2\)
\[κύλινδρος, \quad ισορροπία, \Rightarrow Σ\vecτ = 0\] \[T_1 \cdot r - T_2 \cdot R = 0 \Rightarrow T_1 = 2 \cdot T_2 = 60N\]νήμα (1) αβαρές, μη εκτατό \(T'_1 = T_1\)
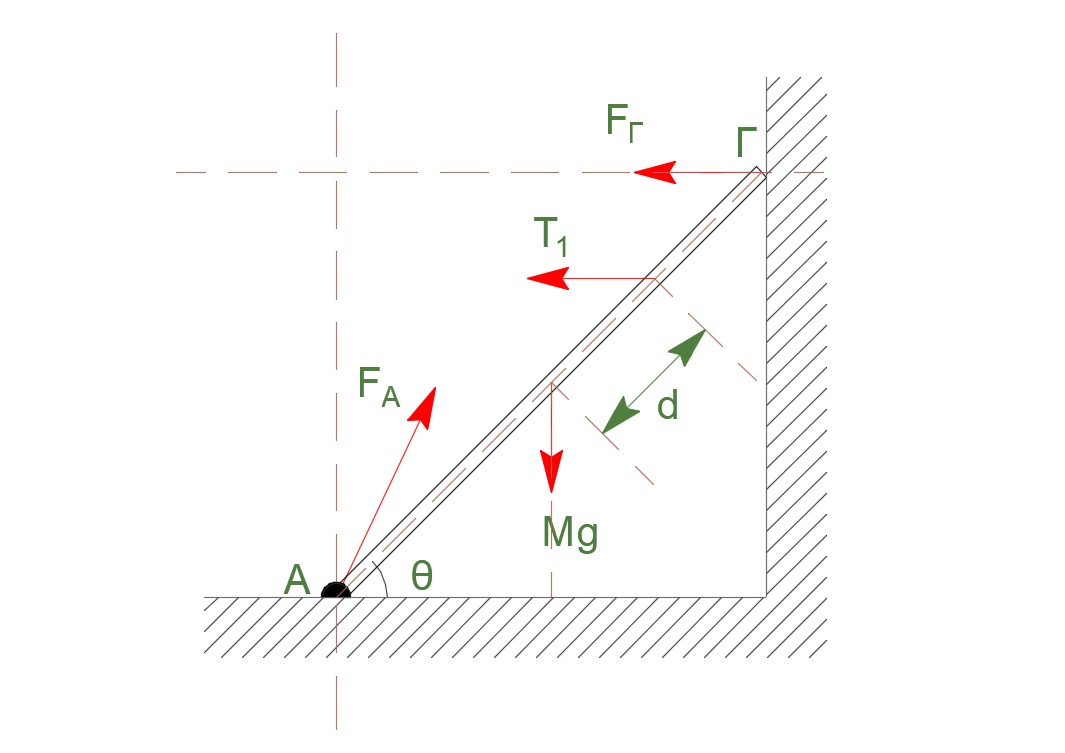
Δ2-\((4)\)
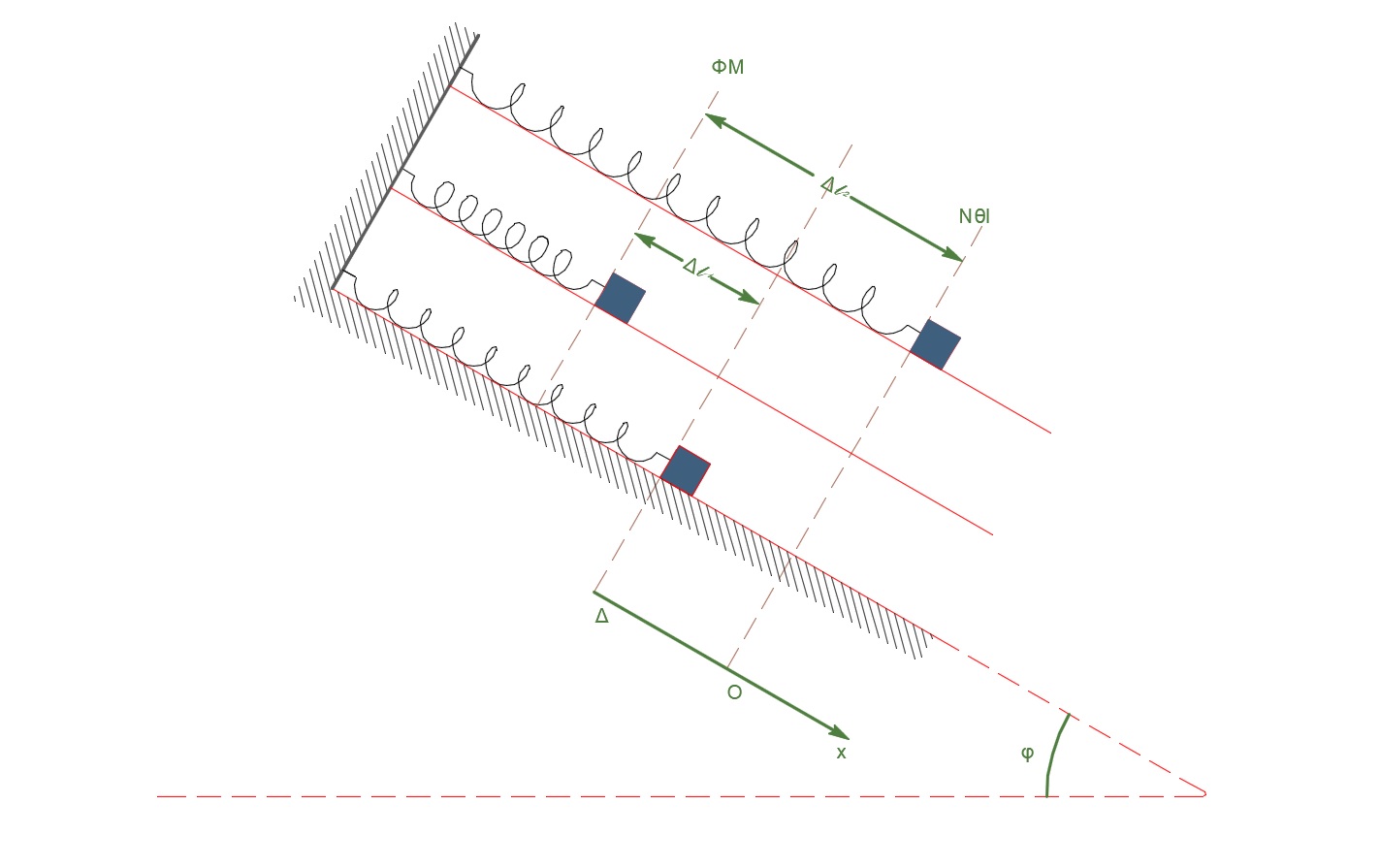
Αρχική θέση ισορροπίας
\[ΣF_x = 0 \Rightarrow F_{ελ1} = m_1 \cdot g \cdot ημφ \Rightarrow Δl_1 = \frac{m_1 \cdot g \cdot ημφ}{k} \Rightarrow Δl_1 = 0.05m\]Νέα θέση ισορροπίας
\[ΣF_x = 0 \Rightarrow F_{ελ2} = (m_1 + m_2) \cdot g \cdot ημφ \Rightarrow Δl_1 = \frac{(m_1 + m_2) \cdot g \cdot ημφ}{k}\] \[Δl_2 = 0.2m\] \[α) \underline {τρόπος}\]Αρχή Διατήρησης Ενέργειας Ταλάντωσης (Ι –> ΙΙ)
\[Κ_Ι + U_I = U_{max} \Rightarrow \frac{1}{2}(m_1+m_2) \cdot V_K^2 + \frac{1}{2} \cdot D \cdot (Δl_2 - Δl_1)^2 = \frac{1}{2} \cdot D \cdot A^2\] \[A =0.3m\] \[β) \underline {τρόπος}\] \[\left. \begin{matrix}x = A \cdot ημ(ωt + φ_ο) \\\\ υ = Α \cdot ω \cdot συν(ωt + φ_ο) \end{matrix} \right\} ημ^2(ωt + φ_ο) + συν^2(ωt + φ_ο) = 0\] \[\frac{x^2}{A^2} + \frac{υ^2}{Α^2 \cdot ω^2} = 1 \Rightarrow A = \sqrt{x^2 + \frac{υ^2}{ω^2}} \Rightarrow A = 0.3m\]Δ3-\((6)\)
\[D=k=(m_1 + m_2)\cdot ω^2 \Rightarrow ω = \sqrt{\frac{k}{m_1+m_2}} \Rightarrow ω = 5 \frac{rad}{s}\] \[t=0, \quad x_Δ = - (ΟΔ) = - (Δl_2 - Δl_1) = -0.15m, \quad υ_Δ = V_k >0\] \[α) \underline {τρόπος}\] \[x = A \cdot ημ(ωt + φ_ο) \overset{t=0}{\implies} -0.15 = 0.3 \cdot ημφ_ο \Rightarrow ημφ_ο = -\frac{1}{2} \Rightarrow ημφ_ο = ημ(\frac{7π}{6})\] \[φ_o = \begin{cases}2k\pi + \frac{7\pi}{6}, & k = 0 \Rightarrow φ_o = \frac{7π}{6} \quad υ = υ_m \cdot συν \frac{7π}{6} < 0, απορρίπτεται \\\ 2k\pi+ \pi - \frac{7\pi}{6}, & k = 1\Rightarrow φ_o = \frac{11π}{6} \quad υ = υ_m \cdot συν \frac{11π}{6} > 0 \quad δεκτή \end{cases}\] \[β) \underline {τρόπος}\]Περιστρεφόμενο διάνυσμα: Έστω \(Σ\) σημείο που εκτελεί \(Ο.Κ.Κ.\) με σταθερή \(ω\), σε κύκλο ακτίνας \(Α\). Η γωνία που διαγράφει η επιβατική ακτίνα δίνεται από την σχέση \(φ = ω \cdot t\)
Η προβολή του σημείου στον κατακόρυφο άξονα δίνεται από την σχέση
\[x = A ημφ \Rightarrow x = A \cdot ημωt\]άρα η προβολή του σημείου \(Σ\) εκτελεί \(Α.Α.Τ.\)
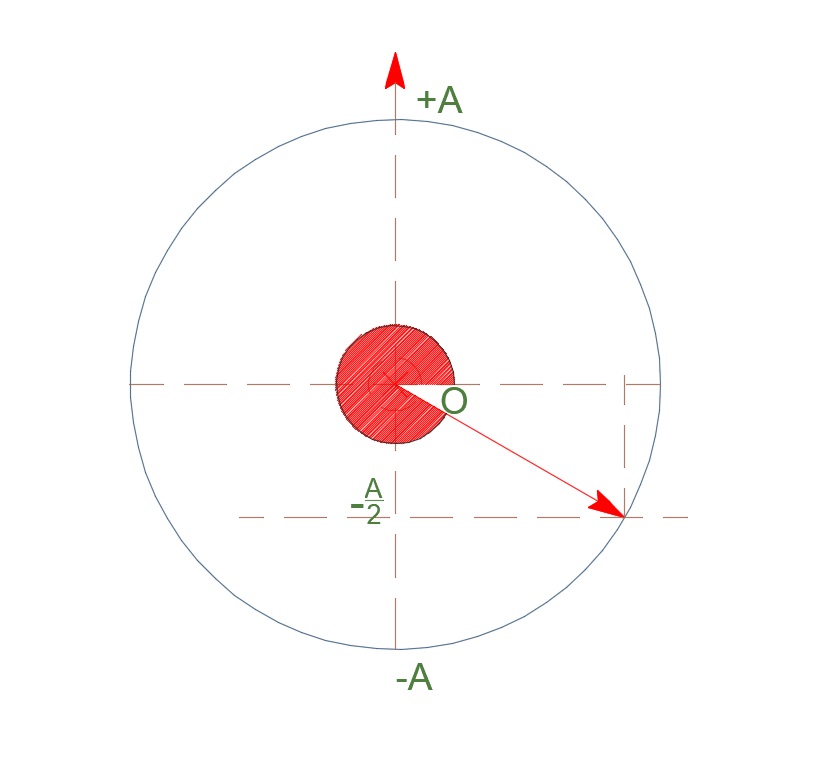
Δ4-\((5)\)
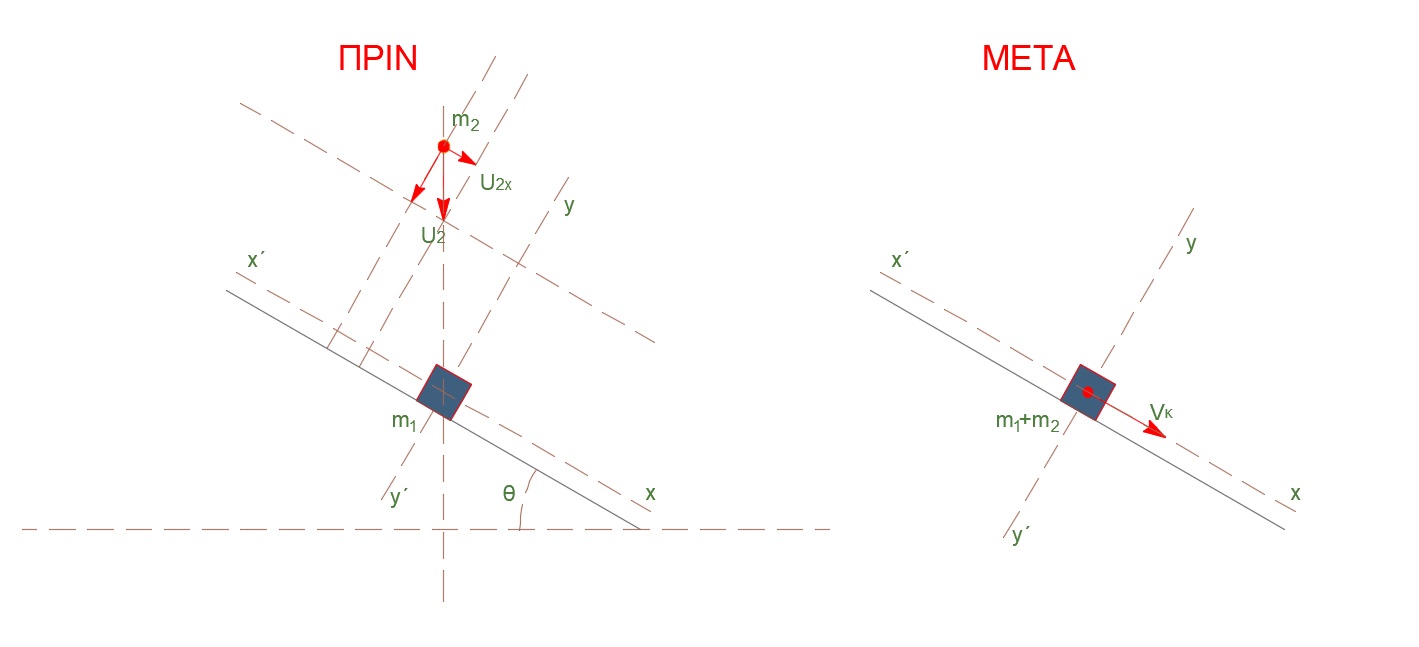
Δ5-\((4)\)
όταν \(x = +A\)
\[|F_{EΠ}| = D \cdot A \Rightarrow F_{επ} = 30Ν\] \[Δl = Δl_2 + A \Rightarrow |F_{ελ}| = k \cdot Δl \Rightarrow F_{ελ} = 50Ν\] \[\frac{|F_{ελ}|}{|F_{επ}|} = \frac{5}{3}\]Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus