Επαναληπτικές 2019
Ενδεικτικές απαντήσεις
Θέμα Α
Α1 - \(β\)
Α2 - \(α\)
Α3 - \(δ\)
Α4 - \(β\)
Α5: \(Σ - Λ - Λ - Σ - Λ\)
Θέμα Β
B1-\((i)\)
\[x_1 = A \cdot ημ(399πt) \quad (S.I.), \quad x_2 = A \cdot ημ(401πt) \quad (S.I.)\] \[ω_1 = 399π \frac{rad}{s}\] \[ω_2 = 401π \frac{rad}{s}\] \[ω_{τελ} = \frac{ω_1 + ω_2}{2} = 400π \frac{rad}{s}, \quad T_{τελ} = \frac{2π}{ω_{τελ}} = \frac{1}{200} sec\] \[T_δ = \frac{2π}{|ω_1 - ω_2|} = \frac{2π}{2π} = 1 sec\] \[σε \quad t=2 \cdot T_δ: \quad N_{ταλ} = \frac{t}{T_{ταλ}} = \frac{2 \cdot 1}{\frac{1}{200}} = 400 ταλαντώσεις\]άρα σωστό το \(i\)
Β2 - \((iii)\)
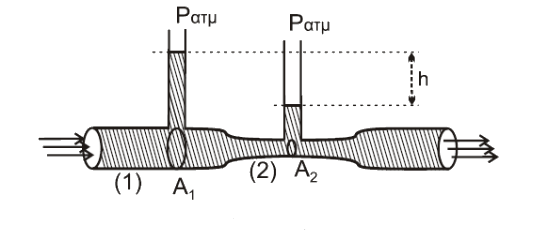
πριν
\[Π_1 = Π_2 \Rightarrow A_1 \cdot υ_1 = Α_2 \cdot υ_2 \overset{\frac{A_1}{Α_2} = 2}{\implies} 2 \cdot υ_1 = υ_2\]Εξίσωση Bernoulli για μια ρευματική γραμμή \((1 \rightarrow 2)\)
\[P_1 + \frac{1}{2}ρ \cdot υ_1^2 = P_2 + \frac{1}{2}ρ \cdot υ_2^2 \Rightarrow P_{ατμ} + ρ \cdot g \cdot h_1 + \frac{1}{2}ρ \cdot υ_1^2 = P_{ατμ} + ρ \cdot g \cdot h_2 + \frac{1}{2}ρ \cdot υ_2^2\] \[ρ \cdot g \cdot (h_1 - h_2) = \frac{3}{2} \cdot ρ \cdot υ_1^2 \Rightarrow g \cdot h = \frac{3}{2} \cdot υ_1^2\]μετά
με ταχύτητα ροής \(υ_1' = 2υ_1\) στην περιοχή (1) θα έχουμε
\[Π_1' = Π_2' \Rightarrow A_1 \cdot υ_1' = Α_2 \cdot υ_2' \overset{\frac{A_1}{Α_2} = 2}{\implies} 2 \cdot υ_1' = υ_2'\]Εξίσωση Bernoulli για μια ρευματική γραμμή \((1' \rightarrow 2)\)
\[P_1 + \frac{1}{2}ρ \cdot υ_1'^2 = P_2 + \frac{1}{2}ρ \cdot υ_2'^2 \Rightarrow P_{ατμ} + ρ \cdot g \cdot h_1' + \frac{1}{2}ρ \cdot υ_1'^2 = P_{ατμ} + ρ \cdot g \cdot h_2' + \frac{1}{2}ρ \cdot υ_2'^2\] \[ρ \cdot g \cdot (h_1' - h_2') = \frac{3}{2} \cdot ρ \cdot υ_1'^2 \Rightarrow g \cdot h' = \frac{3}{2} \cdot υ_1'^2\] \[\frac{g h}{g h'} = \frac{\frac{3}{2} \cdot υ_1^2}{\frac{3}{2} \cdot υ_1'^2} \Rightarrow \frac{h}{h'}= \frac{υ_1^2}{υ_1'^2} \overset{υ_1' = 2υ_1}{\implies} h'=4h\]άρα σωστό το \(iii\)
Β3 - \((ii)\)
πρίν την κρούση
\[p_1 = m \cdot υ, \quad p_2 = 0\]μετά την κρούση
\[p_1' = m \cdot υ_1 \quad p_2' = m \cdot υ_2\] \[Σ\vec{F_{εξ}} = 0 \iff Α.Δ.Ο. \quad \vec{p}_{πριν} = \vec{p}_{μετα}\] \[\vec{p_1} = \vec{p_1}' + \vec{p_2}'\] \[p_1^2 = p_1'^2 + p_2'^2 + 2 \cdot p_1' \cdot p_2' \cdot συνφ \Rightarrow υ^2 = υ_1^2 + υ_2^2 + 2\cdot υ_1 \cdot υ_2 \cdot συνφ\]Διατήρηση Κινητικής Ενέργειας
\[K_{αρχ} = K_{τελ} \Rightarrow \frac{1}{2} \cdot m \cdot υ^2 + 0 = \frac{1}{2} \cdot m \cdot υ_1^2+ \frac{1}{2} \cdot m \cdot υ_2^2 \Rightarrow υ^2 = υ_1^2 + υ_2^2\]οπότε από τις τελευταίες σχέσεις
\[2\cdot υ_1 \cdot υ_2 \cdot συνφ = 0 \Rightarrow συνφ = 0 \Rightarrow φ = 90^ο\]άρα σωστό το \(ii\)
Θέμα Γ
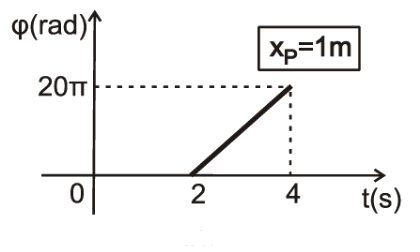
t=2sec
\[φ_ρ = 0 \Rightarrow \frac{2π\cdot 2}{T} - \frac{2π\cdot1}{λ} = 0 \Rightarrow T = 2λ\]t=4sec
\[φ_ρ = 20π \Rightarrow \frac{2π\cdot 4}{T} - \frac{2π\cdot1}{λ} = 20π\] \[\frac{4}{T} - \frac{1}{λ} = 10π \Rightarrow \frac{4}{2λ} - \frac{1}{λ} = 10π \Rightarrow λ = 0,1m\] \[T = 0.2sec \quad ω = \frac{2π}{0,2} = 10π \frac{rad}{s}\]Γ1
\[D = Δm \cdot ω^2 \Rightarrow D = 2π^2 \cdot 10^{-4} \frac{N}{m}\] \[E_T = \frac{1}{2} \cdot D \cdot A^2 \Rightarrow 16π^2 \cdot 10^{-8} = \frac{1}{2} \cdot 2π^2 \cdot 10^{-4} \cdot A^2 \Rightarrow A = 0.04m\]Γ2
\[y = 0.04 \cdot ημ(\frac{2πt}{0.2} - \frac{2πx}{0.1} )\Rightarrow y = 0.04 \cdot ημ(10πt - 20πx) \quad (S.I.)\]Γ3
\[υ_δ = \frac{λ}{Τ} = \frac{0.1}{0.2} = 0.5 \frac{m}{s}\] \[t_Σ = \frac{x_Σ}{υ_δ} = \frac{1.15}{0.5} = 2.3 sec\] \[y_P = 0 \Rightarrow A \cdot ημφ_Ρ \Rightarrow φ_Ρ = 2kπ, υ_Ρ > 0\] \[φ_Ρ = 10πt - 20π \cdot 1.15 = 10πt - 23π \quad (S.I.)\] \[φ_Ρ - φ_Σ = (10πt - 20π) - (10πt - 23π) = 3π rad \overset{φ_Ρ = 2kπ}{\implies} φ_Σ = 2kπ - 3π\] \[υ_Σ = ωΑ \cdot συνφ_Σ = 10π \cdot 0.04 \cdot συν(2kπ - 3π) = 0,4π \cdot (-1) - 0.4π \frac{m}{s}\]Γ4
\[y_Σ\begin{cases} 0 & 0\le t< 2,3s \\\ 0,04 \cdot ημ\left(10πt-23π \right), & t\ge 2.3 sec \end{cases}\]Θέμα Δ
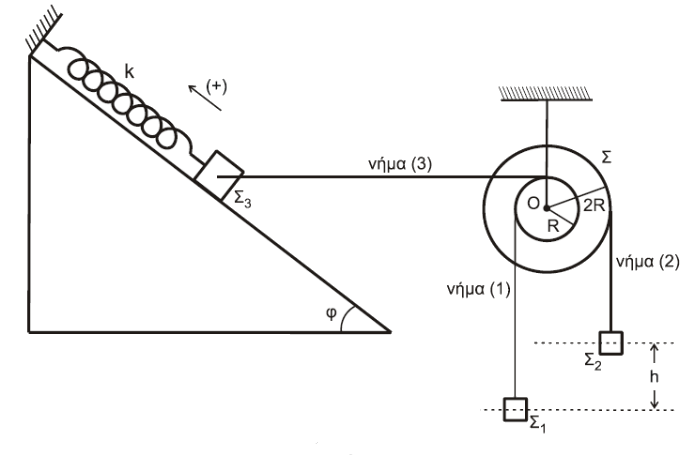
Δ1
\[M_1, \quad ισορροπία, \quad \Rightarrow Σ\vec{F} = 0\] \[T_1 = Μ_1 \cdot g \Rightarrow T_1 = 20N\] \[M_2, \quad ισορροπία, \quad \Rightarrow Σ\vec{F} = 0\] \[T_2 = Μ_2 \cdot g \Rightarrow T_2 = 15N\] \[M_Σ, \quad ισορροπία, \quad \Rightarrow Σ\vecτ_{(K)} = 0\] \[T_2 \cdot 2R = T_1 \cdot R \cdot T_3 \cdot R \Rightarrow T_3 = 20N\] \[M_3, \quad ισορροπία, \quad \Rightarrow Σ \vec{F} = 0\] \[ΣF_x =0 \Rightarrow F_{ελ} - W_{3x} - T_{3x} = 0 \Rightarrow k \cdot Δl = Μ_3 \cdot g \cdot ημφ + Τ_3 \cdot συνφ \Rightarrow Δl = 0.12m\]Δ2
\[D = k = M_3 \cdot ω^2 \Rightarrow ω = 10 \frac{rad}{s}, \quad T = \frac{π}{5} sec\] \[x = A \cdot ημ(ωt + φ_ο)\] \[t=0, \quad υ=0 \quad x_Γ = -Α\] \[Θ.Ι. \quad ΣF_x = 0 \Rightarrow F_{ελ} - W_{3x} = 0 \Rightarrow k \cdot Δl_3 = M_3 \cdot g \cdot ημφ \Rightarrow Δl_3 = 0.08m\] \[Α = Δl_1 - Δl_3 \Rightarrow A = 0.04m\] \[t=0 \Rightarrow -A = A \cdot ημφ_ο \Rightarrow ημφ_ο = ημ\frac{3π}{2} \Rightarrow φ_ο = 2kπ + \frac{3π}{2} \Rightarrow φ_ο = \frac{3π}{2} \frac{rad}{s}\] \[t_1 = \frac{π}{15} sec x_1 = 0.04 \cdot ημ(10 \cdot \frac{π}{15} + \frac{3π}{2} ) \Rightarrow x_1 = 0.02m\] \[\frac{dP}{dt} = ΣF_x = - D \cdot x \overset{t = t_1}{\implies} \frac{dP}{dt} = - D \cdot x_1 \Rightarrow \frac{dP}{dt} = -6N\]Δ3
\[υ_1 = ω \cdot R \Rightarrow a_1 = α_{γων} \cdot R\] \[υ_2 = ω \cdot 2 R \Rightarrow a_2 = α_{γων} \cdot 2R\] \[Μ_2 \quad ΣF = m \cdot a \Rightarrow W_2 - T_2' = M_2 \cdot a_2 \Rightarrow 15 - T_2' = 1.5 \cdot α_{γων} \cdot 0.2\] \[Μ \quad Στ = Ι \cdot α_{γων} \Rightarrow T_2' \cdot 2R - T_1' \cdot R = 2M \cdot R^2 \cdot α_{γων} \Rightarrow T_2' \cdot 2 - T_1' = 2\cdot 1.5 \cdot 0.1 \cdot α_{γων}\] \[Μ_1 \quad ΣF = m \cdot a \Rightarrow Τ_1' - W_1 = M_1 \cdot a_1 \Rightarrow T_1' - 10 = 1 \cdot α_{γων} \cdot 0.1\]Λύση του συστήματος
\[α_{γων} = 20 \frac{rad}{s^2}\]Δ4
\[t_2: \quad h_1 = θ \cdot R \quad h_2 = θ \cdot 2R \overset{h_1 + h_2 = h}{\implies} 3θ \cdot R = h \Rightarrow θ = \frac{h}{3R} = \frac{0.48}{0.3} \Rightarrow θ = 1,6 rad\] \[θ = \frac{1}{2} \cdot α_{γων} t^2 \Rightarrow 1.6 = \frac{1}{2} \cdot 20 \cdot t_2^2 \Rightarrow t_2 = 0.4 sec\] \[ω = α_{γων} \cdot t_2 \Rightarrow ω = 8 \frac{rad}{s}\] \[L = I \cdot α_{γων} = 2Μ \cdot R^2 \cdot α_{γων} \Rightarrow L = 0.24 kg \cdot \frac{m}{s^2}\]Δ5
\[Ν = \frac{θ_3}{2π} \Rightarrow θ_3 = \frac{20}{π} \cdot 2π \Rightarrow θ_3 = 40 rad\] \[θ_3 = \frac{1}{2} α_{γων} t_3^2 \Rightarrow t_3 = 2 sec\] \[ω_3 = α_{γων} t_3 \Rightarrow ω_3 = 40 \frac{rad}{s}\] \[Στ = Ι \cdot α_{γων} = 2 M \cdot R^2 \cdot α_{γων} \Rightarrow Στ = 0,6 N \cdot m\] \[Θ.Μ.Κ.Ε. \quad dK = dW \Rightarrow dK = Στ \cdot dθ \Rightarrow \frac{dK}{dt} = Στ \cdot \frac{dθ}{dt} \overset{t = t_3}{\implies} \frac{dK}{dt} = 24 \frac{J}{s}\]Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus