Μοριοδότηση 2019 - Εσπερινά
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(β\)
Α2 - \(γ\)
Α3 - \(α\)
Α4 - \(γ\)
Α5: \(Λ - Σ - Λ - Σ - Σ\)
Θέμα Β
B1-\((ii)-2-6\)
H πηγή σε κάθε ταλάντωση διέρχεται δύο φορές από την θέση ισορροπίας. \(Ν = 30\)
\[f = \frac{N}{t} = \frac{30}{30} = 1 Hz \Rightarrow T = \frac{1}{f} = 1 s\] \[ω = \frac{2π}{T} \Rightarrow ω = 2π \frac{rad}{s}\] \[2 A = 0.2 \Rightarrow A = 0.1 m\] \[x_Γ = υ_δ \cdot t \Rightarrow x_Γ = υ_δ \cdot 2 T \Rightarrow υ_δ = 0.2 \frac{m}{s}\] \[\frac{υ_{max}}{υ_δ} = \frac{A\cdot ω}{υ_δ} = \frac{0.2π}{0.2} = π\]άρα σωστό το \(ii\)
Β2 - \((iii)-2-7\)
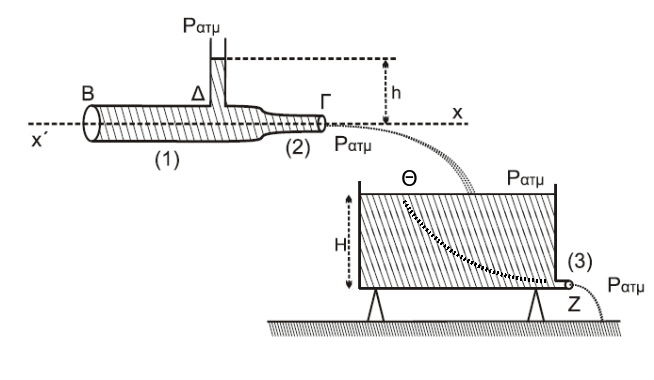
Όταν σταθεροποιείται το ύψος στο δοχείο
\[Π_2 = Π_3 \Rightarrow A_2 \cdot υ_2 = Α_3 \cdot υ_3 \overset{Α_3= \frac{A_2}{2}}{\implies} υ_2 = \frac{υ_3}{2}\]Εξίσωση Bernoulli για μια ρευματική γραμμή \((Θ \rightarrow Z)\)
\[P_Θ + \frac{1}{2}ρ \cdot υ_Θ^2 + ρ \cdot g \cdot H = P_Z + \frac{1}{2}ρ \cdot υ_3^2 \Rightarrow P_{ατμ} + ρ \cdot g \cdot H = P_{ατμ} + \frac{1}{2}ρ \cdot υ_3^2\] \[υ_3 = \sqrt{2 \cdot g \cdot H}\]Εξίσωση συνέχειας \((Δ \rightarrow Γ)\)
\[Π_1 = Π_2 \Rightarrow Α_1 \cdot υ_1 = Α_2 \cdot υ_2 \overset{Α_1 = 2Α_2}{\implies} υ_2 = 2υ_1\]Εξίσωση Bernoulli για μια οριζόντια ρευματική γραμμή \((Δ \rightarrow Γ)\)
\[P_Δ + \frac{1}{2}ρ \cdot υ_1^2 = P_2 + \frac{1}{2}ρ \cdot υ_2^2\] \[P_Δ = P_{ατμ} + ρ \cdot g \cdot h\] \[P_{ατμ} + ρ \cdot g \cdot h + \frac{1}{2}ρ \cdot υ_1^2 = P_{ατμ} + \frac{1}{2}ρ \cdot υ_2^2 \Rightarrow g \cdot h = \frac{1}{2} \cdot (υ_2^2 - υ_1^2)\] \[g \cdot h = \frac{3}{8} \cdot υ_2^2 \overset{υ_2 = \frac{υ_3}{2}}{\implies} g \cdot h = \frac{3}{8} \cdot \frac{υ_3^2}{4}\] \[υ_3^2 = \frac{32}{3} \cdot g \cdot h \overset{υ_3 = \sqrt{2 \cdot g \cdot H}}{\implies} 2 \cdot g \cdot H = \frac{32}{3} \cdot g \cdot h \Rightarrow \frac{h}{H} = \frac{3}{16}\]άρα σωστό το \(iii\)
Β3 - \((i)-2-6\)
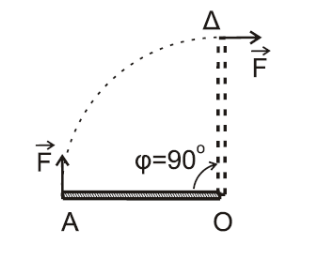
άρα σωστό το \(i\)
Θέμα Γ
Γ1-\((6)\)
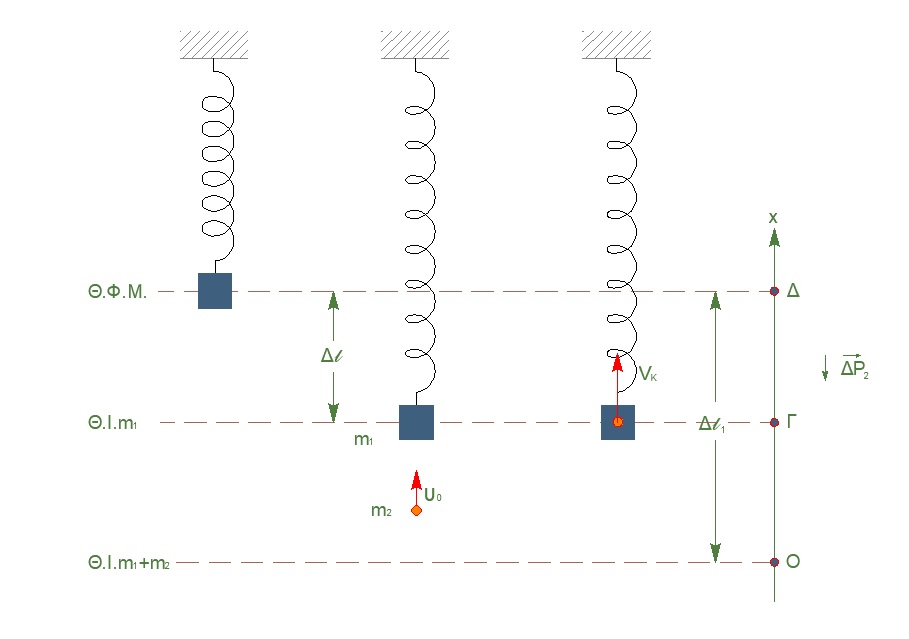
Στην ακραία θέση \(υ_{ταλ} = 0 \Rightarrow A = 0.1m\)
Γ2-\((6)\)
\[α) \underline {τρόπος}\] \[ΑΔΕ_{ταλ} (Γ \rightarrow Δ)\] \[K_Γ + U_{ταλΓ} = K_Δ + U_{ταλΔ} \Rightarrow \frac{1}{2} \cdot (m_1 + m_2) \cdot V_k^2 + \frac{1}{2} \cdot D \cdot (Δl_1 - Δl)^2 = 0 + \frac{1}{2} \cdot D \cdot A^2\] \[2V_k^2 + 200 \cdot 0.05^2 = 200 \cdot 0.01 \Rightarrow V_k^2 + 0.25 = 1 \Rightarrow V_k = \sqrt{0.75} \Rightarrow |V_k| = 0.5 \sqrt3 \frac{m}{s}, V_k > 0\] \[β) \underline {τρόπος}\] \[ΘΜΚΕ_{(Γ \rightarrow Δ)} \quad ΔΚ = ΣW\] \[K_Δ - Κ_Γ = W_B + W_{F_{ελ}} \Rightarrow 0 - \frac{1}{2} \cdot (m_1 + m_2) \cdot V_k^2 = -(m_1 +m_2) \cdot g \cdot Δl + \frac{1}{2} \cdot k \cdot Δl^2\] \[-V_k^2 = -1 + 0.25 \Rightarrow V_k = \sqrt{0.75} \Rightarrow |V_k| = 0.5 \sqrt3 \frac{m}{s}\] \[γ) \underline {τρόπος}\] \[D = k = (m_1 + m_2) \cdot ω^2 \Rightarrow ω = \sqrt{\frac{k}{m_1 + m_2}} \Rightarrow ω = 10 \frac{rad}{s}\] \[x = A \cdot ημφ(ωt + φ_ο) \Rightarrow ημ(ωt + φ_ο) = \frac{x}{A}\] \[υ = Αω \cdot συνφ(ωt + φ_ο) \Rightarrow συν(ωt + φ_ο) = \frac{υ}{Aω}\] \[ημ^2φ + συν^2φ = 1 \Rightarrow \frac{x^2}{A^2} + \frac{υ^2}{A^2ω^2}\] \[\frac{\frac{A^2}{4}}{A^2} + \frac{υ^2}{A^2ω^2} \Rightarrow υ = \frac{\sqrt3}{2} \Rightarrow V_k = \frac{\sqrt3}{2} \frac{m}{s}\] \[Σ\vec{F_{εξ}} = 0 \iff Α.Δ.Ο. \quad \vec{p}_{πριν} = \vec{p}_{μετα}\] \[m_2 \cdot u_o = (m_1 + m_2) \cdot V_k \Rightarrow u_o = \sqrt3 \frac{m}{s}\]Γ3-\((6)\)
\[ΔΕ_Μ = Ε_Μ^{αρχ} - Ε_Μ^{τελ} = Κ_{αρχ} - Κ_{τελ} = \frac{1}{2} \cdot m_2 \cdot u_o^2 - \frac{1}{2} \cdot (m_1 + m_2) \cdot V_K^2\] \[ΔΕ_Μ = 1.5 - 0.75 \Rightarrow ΔΕ_Μ = 0.75 J\]Γ4-\((7)\)
\[D = k = (m_1 + m_2) \cdot ω^2 \Rightarrow ω = \sqrt{\frac{k}{m_1 + m_2}} \Rightarrow ω = 10 \frac{rad}{s}\] \[α) \underline {τρόπος}\] \[t_o = 0, \quad y = +\frac{A}{2}, \quad υ > 0\] \[y = A \cdot ημ(ωt + φ_ο) \Rightarrow \frac{A}{2} = A \cdot ημφ_ο\] \[ημφ_ο=\frac{1}{2}\Rightarrow ημφ_ο = ημ \frac{π}{6} \Rightarrow φ_o = \begin{cases}2k\pi+\frac{\pi}{6}, & k = 0\Rightarrow φ_o = \frac{π}{6} \quad συνφ_ο > 0 \\\ 2k\pi + \frac{5\pi}{6}, & k = 0 \Rightarrow φ_o = \frac{5π}{6} \quad συνφ_ο < 0, απορρίπτεται \end{cases}\] \[β) \underline {τρόπος}\]Περιστρεφόμενο διάνυσμα: Έστω \(Σ\) σημείο που εκτελεί \(Ο.Κ.Κ.\) με σταθερή \(ω\), σε κύκλο ακτίνας \(Α\). Η γωνία που διαγράφει η επιβατική ακτίνα δίνεται από την σχέση \(φ = ω \cdot τ\)
Η προβολή του σημείου στον κατακόρυφο άξονα δίνεται από την σχέση
\[x = A ημφ \Rightarrow x = A \cdot ημωt\]άρα η προβολή του σημείου \(Σ\) εκτελεί \(Α.Α.Τ.\)
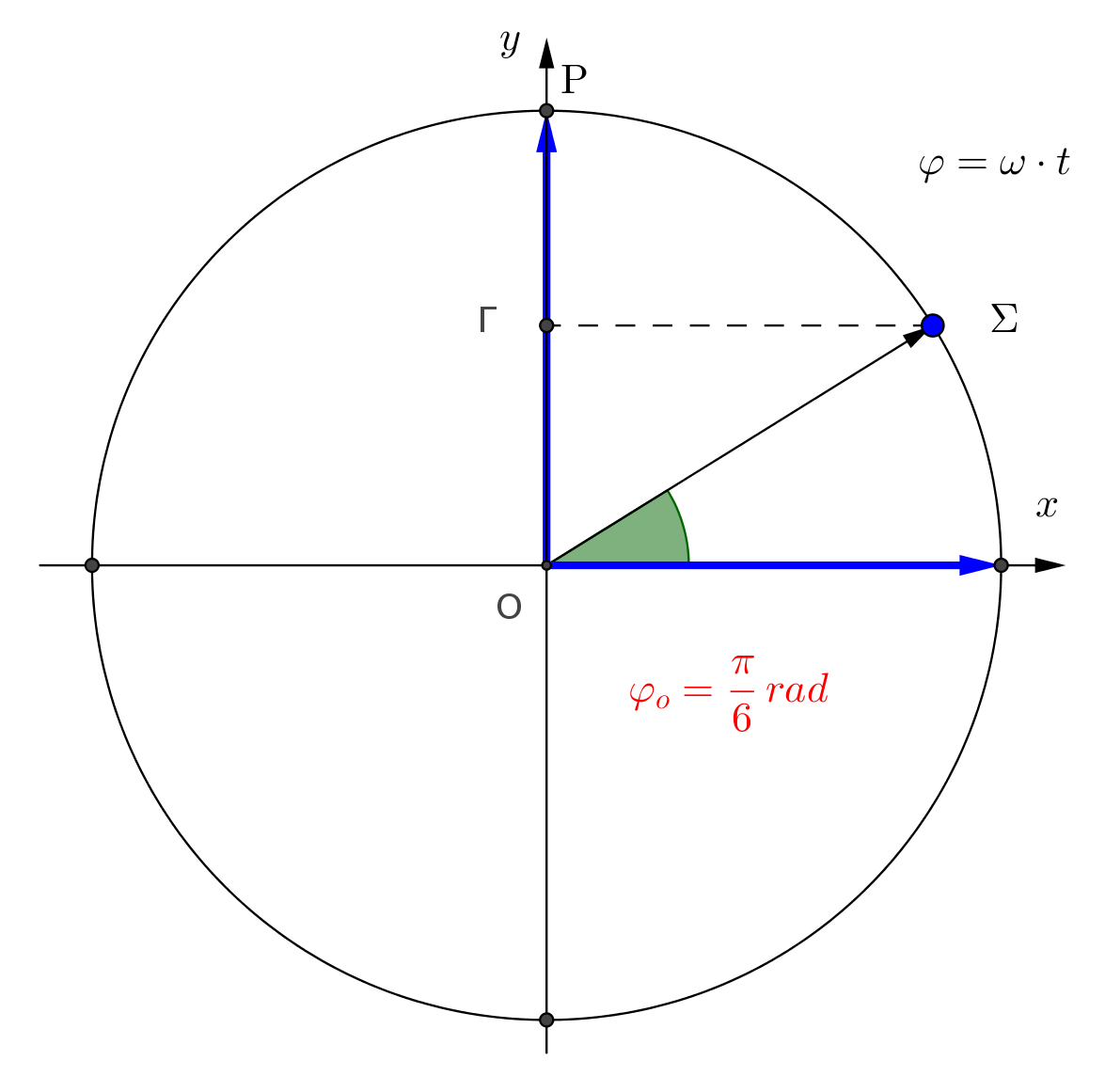
Αρχική φάση \(φ_ο\)
\[ημφ_ο = \frac{y}{A} \Rightarrow ημφ_ο = \frac{+\frac{A}{2}}{A} \Rightarrow ημφ_ο = \frac{1}{2} \Rightarrow φ_o = \frac{π}{6} rad\] \[y = 0.1 \cdot ημ(10t + \frac{π}{6} ), \quad S.I.\]Θέμα Δ
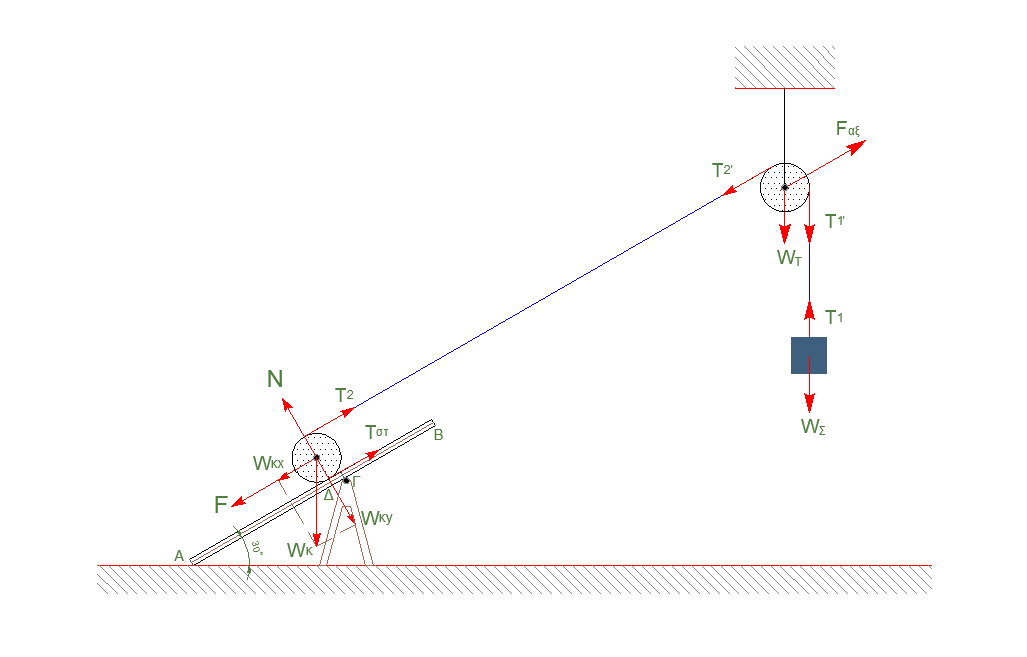
Δ1-\((5)\)
\[M_Σ, \quad ισορροπία, \Rightarrow Σ\vec{F} = 0\] \[T_1 = Μ_Σ \cdot g \Rightarrow T_1 = 20N\] \[M_T, \quad ισορροπία, \Rightarrow Σ\vecτ = 0\] \[T_1 \cdot R_T = T_2 \cdot R_T \Rightarrow T_2 = 20N\] \[α) \underline {τρόπος}\] \[M_K, \quad ισορροπία, \Rightarrow Σ\vecτ_{(K)} = 0\] \[T_2 \cdot R_K = T_{στ} \cdot R_Κ \Rightarrow T_2 = Τ_{στ}\] \[M_K, \quad ισορροπία, \Rightarrow Σ \vec{F} = 0\] \[T_2 + Τ_{στ} = F + Μ_Κ \cdot g \cdot ημφ \Rightarrow 2T_2 = F +10 \Rightarrow F = 30N\] \[β) \underline {τρόπος}\] \[M_K, \quad ισορροπία, \Rightarrow Σ\vecτ_{(Δ)} = 0\] \[T_2 \cdot 2 \cdot R_K = (F + Μ_Κ \cdot g \cdot ημφ) \cdot R_K \Rightarrow 40 = F +10 \Rightarrow F = 30N\]Δ2-\((6)\)
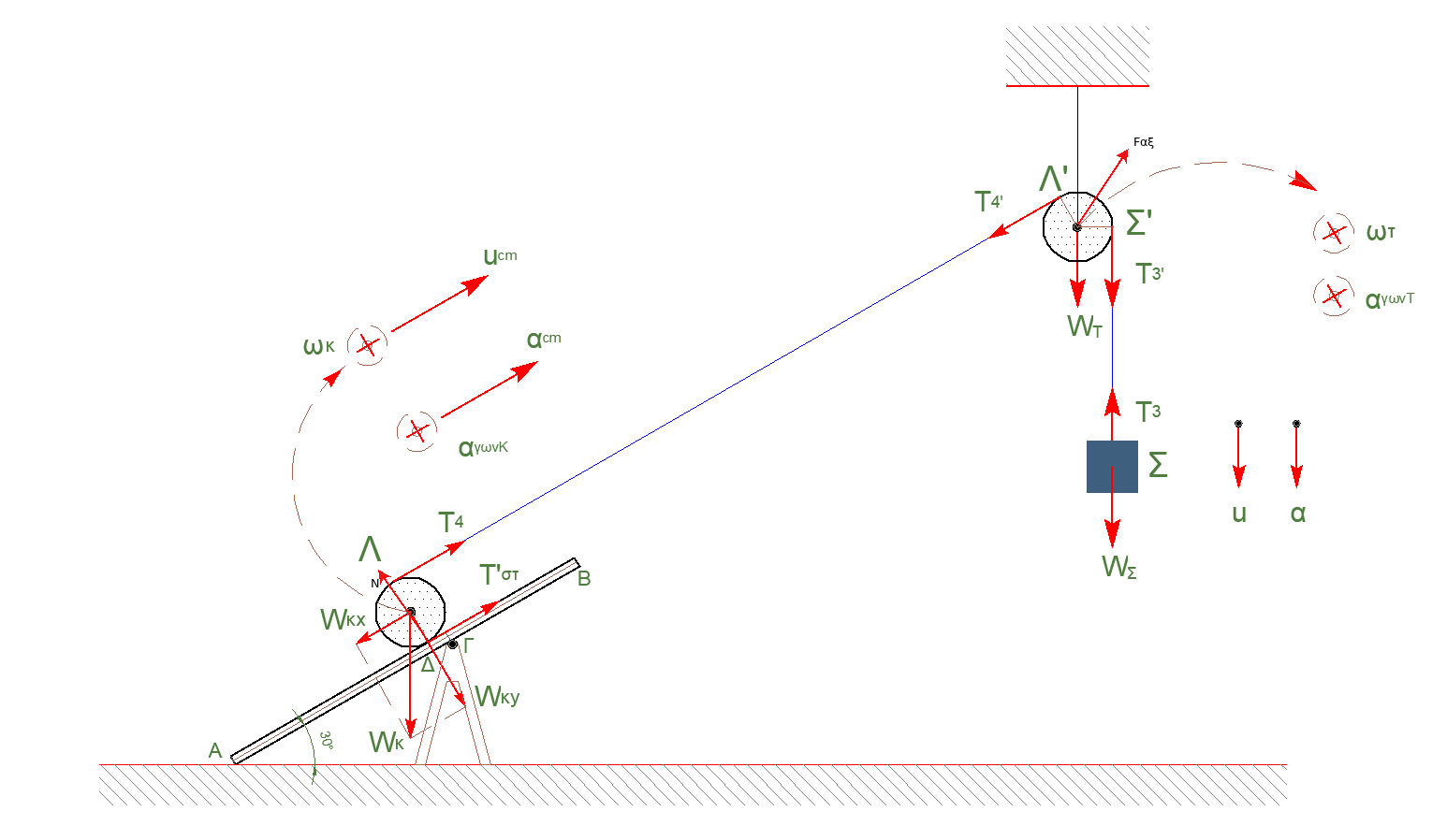
νήμα κατακόρυφο αβαρές, μη εκτατό
\[α_Σ = α_Σ' = α_{γρ} = α_{γων_Τ} \cdot R_T \Rightarrow α_Σ = α_{γων_Τ} \cdot R_T \quad (1)\]νήμα πλάγιο αβαρές, μη εκτατό
\[α_Λ = α_Λ' = α_{γρ} = α_{γων_Τ} \cdot R_T \Rightarrow α_Λ = α_{γων_Τ} \cdot R_T \quad (2)\]Κύλινδρος \(Κ.Χ.Ο.\)
\[υ_Α = 0 \Rightarrow υ_{cm} = ω \cdot R_K \Rightarrow α_{cm} = α_{γων_Κ} \cdot R_K \quad (3)\] \[υ_Λ = υ_{cm} + ω \cdot R_K \Rightarrow υ_Λ = 2 \cdot υ_{cm} \Rightarrow α_Λ = 2 \cdot α_{cm} \quad (4)\] \[M_Σ: \quad METΑΦΟΡΙΚΗ \Rightarrow Σ\vec{F} = M_Σ \cdot \vec{α_Σ}\] \[Μ_Σ \cdot g - T_3 = M_Σ \cdot α_Σ \Rightarrow 20 - T_3 = 2 \cdot α_Σ \quad (5)\] \[M_T: \quad ΣΤΡΟΦΙΚΗ \Rightarrow Σ\vecτ = Ι_T \cdot \vecα_{γων_Τ}\] \[T_3' \cdot R_T - T_4' \cdot R_T = \frac{1}{2} \cdot M_T \cdot R_T^2 \cdot α_{γων_T} \overset{(2)}{\implies} T_3 - T_4 = R_T \cdot α_{γων_Τ} \quad (6)\] \[α) \underline {τρόπος}\] \[M_Κ: \quad METΑΦΟΡΙΚΗ \Rightarrow Σ\vec{F} = Μ_Κ \cdot \vecα_{cm}\] \[T_4 + T_{στ} - Μ_Κ \cdot g \cdot ημφ = Μ_Κ \cdot α_{cm} \Rightarrow T_4 + T_{στ} - 10 = 2\cdot α_{cm} \quad (7)\] \[M_K: \quad ΣΤΡΟΦΙΚΗ \Rightarrow Σ\vecτ = Ι_K \cdot \vecα_{γων_K}\] \[T_4 \cdot R_K - T_{στ} \cdot R_Κ = \frac{1}{2} \cdot M_Κ \cdot R_Κ^2 \cdot α_{γων_Κ} \Rightarrow T_4 - T_{στ} = R_K \cdot α_{γων_Κ} \quad (8)\] \[β) \underline {τρόπος}\] \[Ι_{Κ(Δ)} = Ι_{cm} + M_Κ \cdot R_K^2 \Rightarrow Ι_{Κ(Δ)} = \frac{3}{2} \cdot M_K \cdot R_K^2 (7)\] \[M_K: \quad ΣΤΡΟΦΙΚΗ \Rightarrow Σ\vecτ = Ι_{K_Δ} \cdot \vecα_{γων_Δ}\] \[T_4 \cdot 2 \cdot R_K - M_Κ \cdot g \cdot ημφ \cdot R_Κ = \frac{3}{2} \cdot M_Κ \cdot R_Κ^2 \cdot α_{γων_Δ} \Rightarrow 2\cdot T_4 - 10 = 3 \cdot R_K \cdot α_{γων_Δ} \quad (8)\]Λύση του μη γραμμικού συστήματος των \(8\) εξισώσεων με τους \(10\) αγνώστους \(α_Σ = 4 \frac{m}{s^2}\)
\[α_{cm} = \frac{α_Σ}{2} \Rightarrow α_{cm} = 2 \frac{m}{s^2}\]Δ3-\((7)\)
\[T_4 + T_{στ} - 10 = 2\cdot α_{cm} \Rightarrow T_4 + T_{στ} =14 \quad (1)\] \[T_4 - T_{στ} = α_{cm} \Rightarrow T_4 - T_{στ} = 2 \quad (2)\]Λύση του συστήματος \(Τ_4 = 8Ν, \quad Τ_{στατ} = 6Ν\)
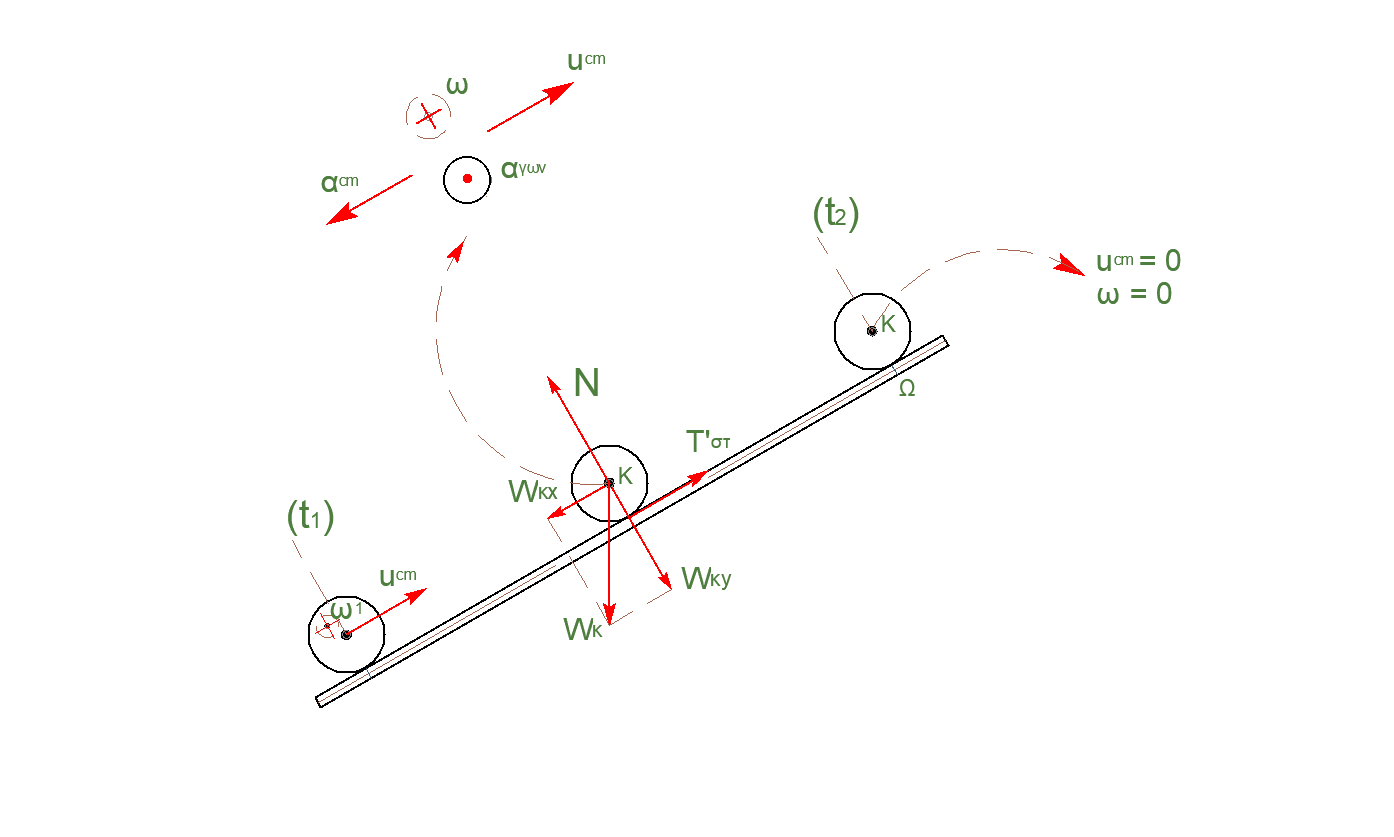
Δ4-\((7)\)
Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus