Μοριοδότηση 2019
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(β\)
Α2 - \(γ\)
Α3 - \(α\)
Α4 - \(γ\)
Α5: \(Λ - Σ - Λ - Σ - Σ\)
Θέμα Β
B1-\((ii)-2-6\)
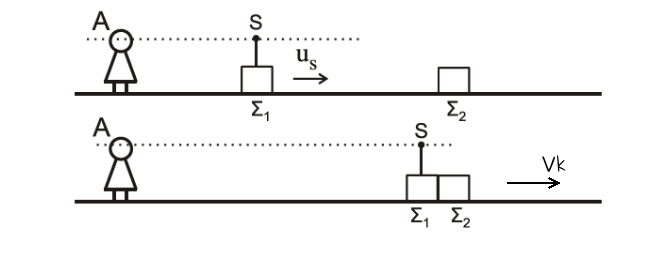
άρα σωστό το \(ii\)
Β2 - \((iii)-2-6\)
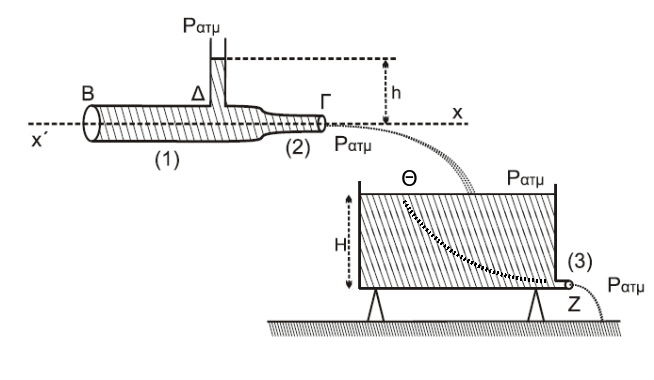
Όταν σταθεροποιείται το ύψος στο δοχείο
\[Π_2 = Π_3 \Rightarrow A_2 \cdot υ_2 = Α_3 \cdot υ_3 \overset{Α_3= \frac{A_2}{2}}{\implies} υ_2 = \frac{υ_3}{2}\]Εξίσωση Bernoulli για μια ρευματική γραμμή \((Θ \rightarrow Z)\)
\[P_Θ + \frac{1}{2}ρ \cdot υ_Θ^2 + ρ \cdot g \cdot H = P_Z + \frac{1}{2}ρ \cdot υ_3^2 \Rightarrow P_{ατμ} + ρ \cdot g \cdot H = P_{ατμ} + \frac{1}{2}ρ \cdot υ_3^2\] \[υ_3 = \sqrt{2 \cdot g \cdot H}\]Εξίσωση συνέχειας \((Δ \rightarrow Γ)\)
\[Π_1 = Π_2 \Rightarrow Α_1 \cdot υ_1 = Α_2 \cdot υ_2 \overset{Α_1 = 2Α_2}{\implies} υ_2 = 2υ_1\]Εξίσωση Bernoulli για μια οριζόντια ρευματική γραμμή \((Δ \rightarrow Γ)\)
\[P_Δ + \frac{1}{2}ρ \cdot υ_1^2 = P_2 + \frac{1}{2}ρ \cdot υ_2^2\] \[P_Δ = P_{ατμ} + ρ \cdot g \cdot h\] \[P_{ατμ} + ρ \cdot g \cdot h + \frac{1}{2}ρ \cdot υ_1^2 = P_{ατμ} + \frac{1}{2}ρ \cdot υ_2^2 \Rightarrow g \cdot h = \frac{1}{2} \cdot (υ_2^2 - υ_1^2)\] \[g \cdot h = \frac{3}{8} \cdot υ_2^2 \overset{υ_2 = \frac{υ_3}{2}}{\implies} g \cdot h = \frac{3}{8} \cdot \frac{υ_3^2}{4}\] \[υ_3^2 = \frac{32}{3} \cdot g \cdot h \overset{υ_3 = \sqrt{2 \cdot g \cdot H}}{\implies} 2 \cdot g \cdot H = \frac{32}{3} \cdot g \cdot h \Rightarrow \frac{h}{H} = \frac{3}{16}\]άρα σωστό το \(iii\)
Β3 - \((ii)-2-7\)
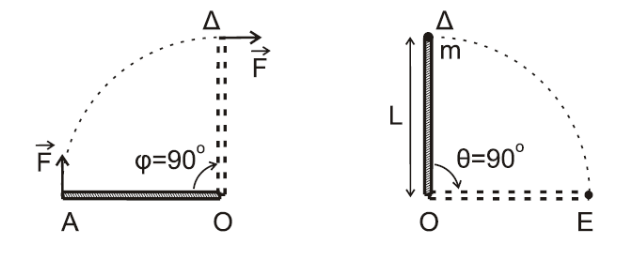
Ομαλή στροφική κίνηση
\[Δθ = ω_k \cdot Δt \Rightarrow Δt = \frac{Δθ}{ω_k} = \frac{Δθ}{\frac{ω}{2}} = \frac{2Δθ}{ω} = \frac{2\cdot \frac{π}{2}}{ω} = \frac{π}{ω}\] \[Δt = \frac{1}{3} s\]άρα σωστό το \(ii\)
Θέμα Γ
Γ1-\((6)\)
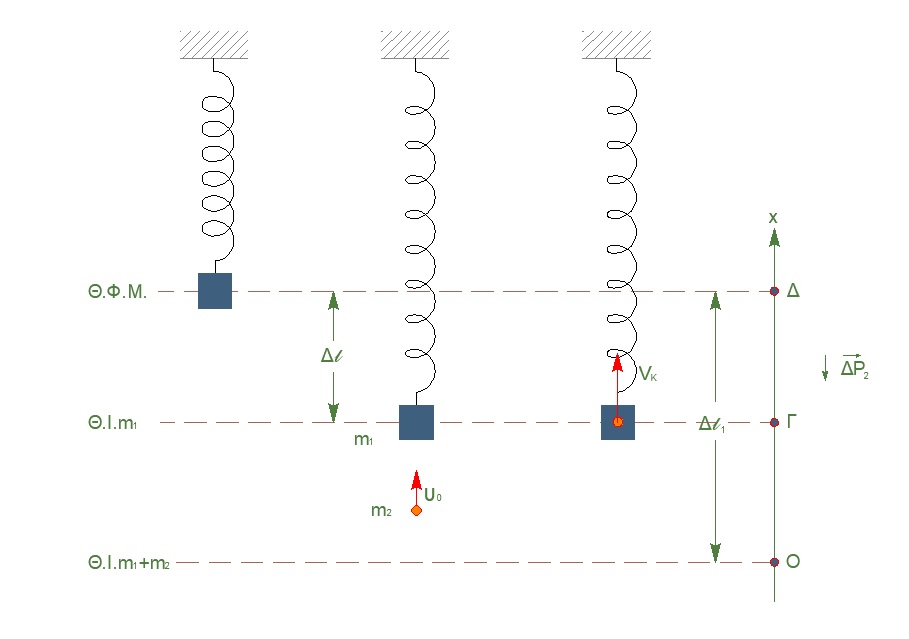
Στην ακραία θέση \(υ_{ταλ} = 0 \Rightarrow A = 0.1m\)
Γ2-\((7)\)
\[Σ\vec{F_{εξ}} = 0 \iff Α.Δ.Ο. \quad \vec{p}_{πριν} = \vec{p}_{μετα}\] \[m_2 \cdot u_o = (m_1 + m_2) \cdot V_k\] \[α) \underline {τρόπος}\] \[ΑΔΕ_{ταλ} (Γ \rightarrow Δ)\] \[K_Γ + U_{ταλΓ} = K_Δ + U_{ταλΔ} \Rightarrow \frac{1}{2} \cdot (m_1 + m_2) \cdot V_k^2 + \frac{1}{2} \cdot D \cdot (Δl_1 - Δl)^2 = 0 + \frac{1}{2} \cdot D \cdot A^2\] \[2V_k^2 + 200 \cdot 0.05^2 = 200 \cdot 0.01 \Rightarrow V_k^2 + 0.25 = 1 \Rightarrow V_k = \sqrt{0.75} \Rightarrow |V_k| = 0.5 \sqrt3 \frac{m}{s}, V_k > 0\] \[β) \underline {τρόπος}\] \[ΘΜΚΕ_{(Γ \rightarrow Δ)} \quad ΔΚ = ΣW\] \[K_Δ - Κ_Γ = W_B + W_{F_{ελ}} \Rightarrow 0 - \frac{1}{2} \cdot (m_1 + m_2) \cdot V_k^2 = -(m_1 +m_2) \cdot g \cdot Δl + \frac{1}{2} \cdot k \cdot Δl^2\] \[-V_k^2 = -1 + 0.25 \Rightarrow V_k = \sqrt{0.75} \Rightarrow |V_k| = 0.5 \sqrt3 \frac{m}{s}\] \[γ) \underline {τρόπος}\] \[D = k = (m_1 + m_2) \cdot ω^2 \Rightarrow ω = \sqrt{\frac{k}{m_1 + m_2}} \Rightarrow ω = 10 \frac{rad}{s}\] \[x = A \cdot ημφ(ωt + φ_ο) \Rightarrow ημ(ωt + φ_ο) = \frac{x}{A}\] \[υ = Αω \cdot συνφ(ωt + φ_ο) \Rightarrow συν(ωt + φ_ο) = \frac{υ}{Aω}\] \[ημ^2φ + συν^2φ = 1 \Rightarrow \frac{x^2}{A^2} + \frac{υ^2}{A^2ω^2}\] \[\frac{\frac{A^2}{4}}{A^2} + \frac{υ^2}{A^2ω^2} \Rightarrow υ = \frac{\sqrt3}{2} \Rightarrow V_k = \frac{\sqrt3}{2} \frac{m}{s}\] \[K_2 = \frac{1}{2} \cdot m_2 \cdot u_o^2 \Rightarrow K_2 = 1.5 J\]Γ3-\((6)\)
\[Δ\vec{p_2} = \vec{p}_{τελ} - \vec{p}_{αρχ} \Rightarrow Δp_2 = m_2 \cdot V_k - m_2 \cdot u_o \Rightarrow Δp_2 = 0.5 \sqrt3 - \sqrt3 \Rightarrow Δp_2 = -0.5\sqrt3 kg \cdot \frac{m}{s}\] \[|Δ\vec{p_2}| = 0.5\sqrt3 kg \cdot \frac{m}{s}\]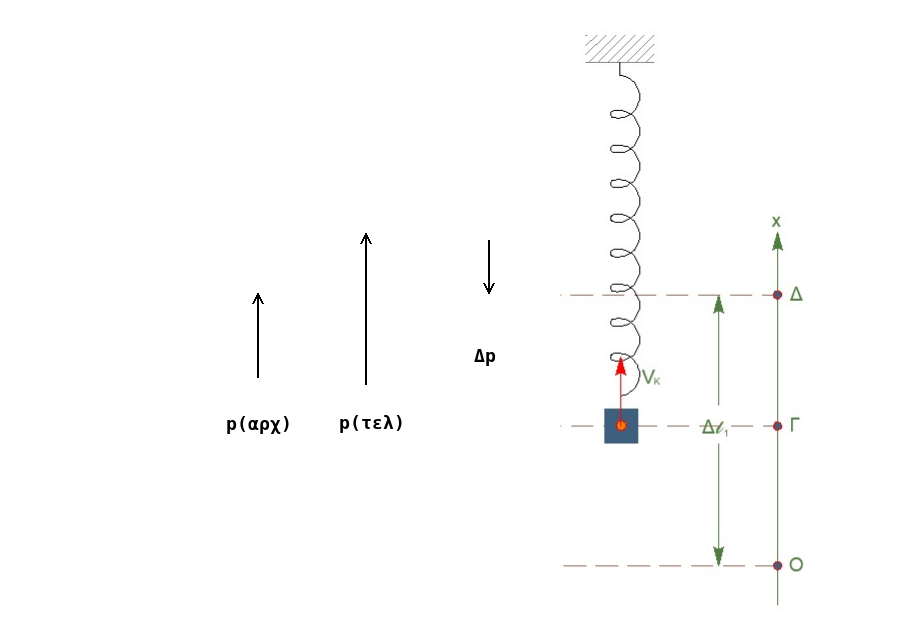
Το πρόσημο δηλώνει την κατεύθυνση του διανύσματος. (σχήμα)
Γ4-\((6)\)
\[D = k = (m_1 + m_2) \cdot ω^2 \Rightarrow ω = \sqrt{\frac{k}{m_1 + m_2}} \Rightarrow ω = 10 \frac{rad}{s}\] \[α) \underline {τρόπος}\] \[t_o = 0, \quad y = +\frac{A}{2}, \quad υ > 0\] \[y = A \cdot ημ(ωt + φ_ο) \Rightarrow \frac{A}{2} = A \cdot ημφ_ο\] \[ημφ_ο=\frac{1}{2}\Rightarrow ημφ_ο = ημ \frac{π}{6} \Rightarrow φ_o = \begin{cases}2k\pi+\frac{\pi}{6}, & k = 0\Rightarrow φ_o = \frac{π}{6} \quad υ = υ_m \cdot συν \frac{π}{6} > 0 \\\ 2k\pi + \frac{5\pi}{6}, & k = 0 \Rightarrow φ_o = \frac{5π}{6} \quad υ = υ_m \cdot συν \frac{5π}{6} < 0, απορρίπτεται \end{cases}\] \[β) \underline {τρόπος}\]Περιστρεφόμενο διάνυσμα: Έστω \(Σ\) σημείο που εκτελεί \(Ο.Κ.Κ.\) με σταθερή \(ω\), σε κύκλο ακτίνας \(Α\). Η γωνία που διαγράφει η επιβατική ακτίνα δίνεται από την σχέση \(φ = ω \cdot t\)
Η προβολή του σημείου στον κατακόρυφο άξονα δίνεται από την σχέση
\[x = A ημφ \Rightarrow x = A \cdot ημωt\]άρα η προβολή του σημείου \(Σ\) εκτελεί \(Α.Α.Τ.\)
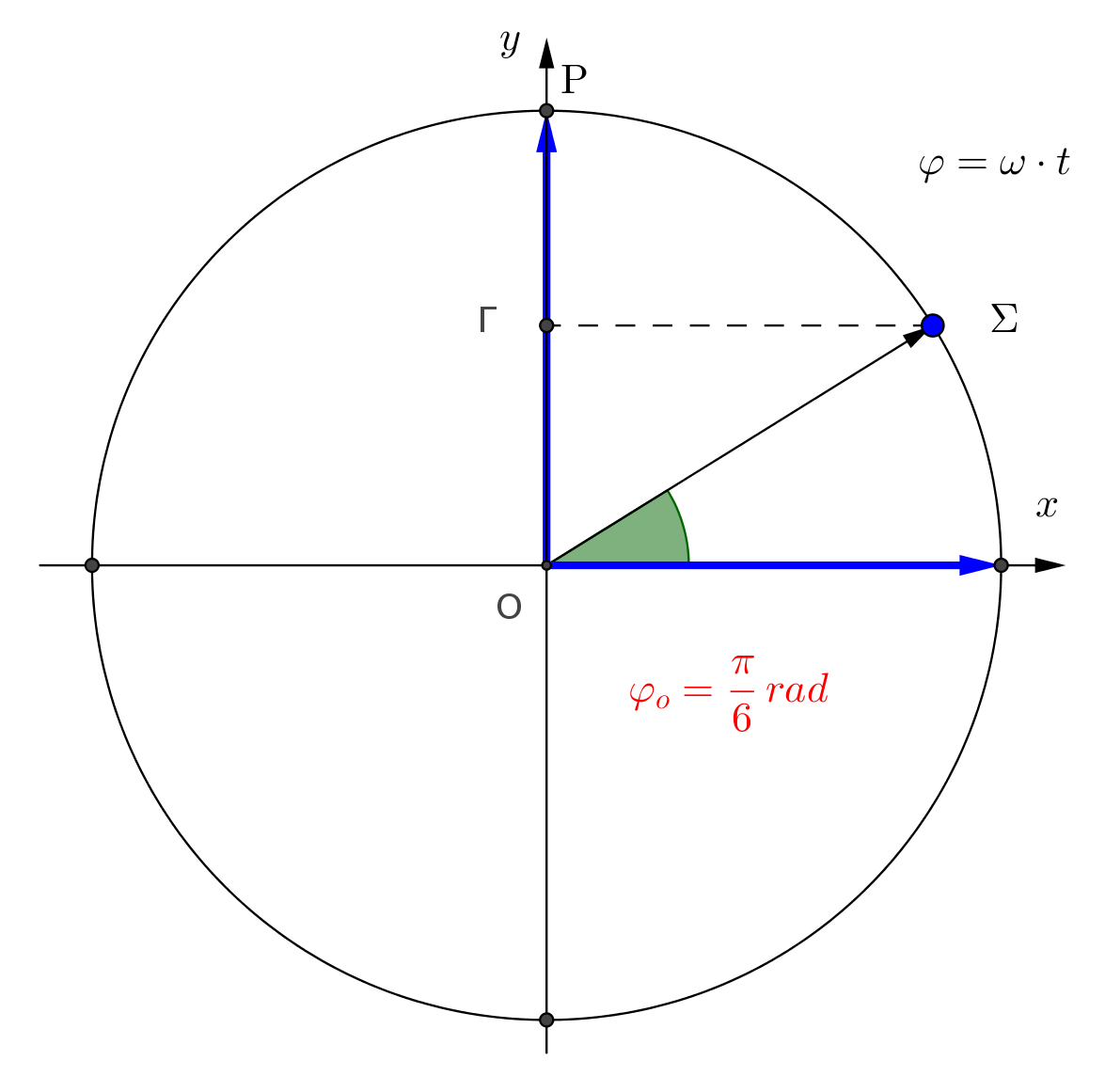
Αρχική φάση \(φ_ο\)
\[ημφ_ο = \frac{y}{A} \Rightarrow ημφ_ο = \frac{+\frac{A}{2}}{A} \Rightarrow ημφ_ο = \frac{1}{2} \Rightarrow φ_o = \frac{π}{6} rad\] \[y = 0.1 \cdot ημ(10t + \frac{π}{6} ), \quad S.I.\]Θέμα Δ
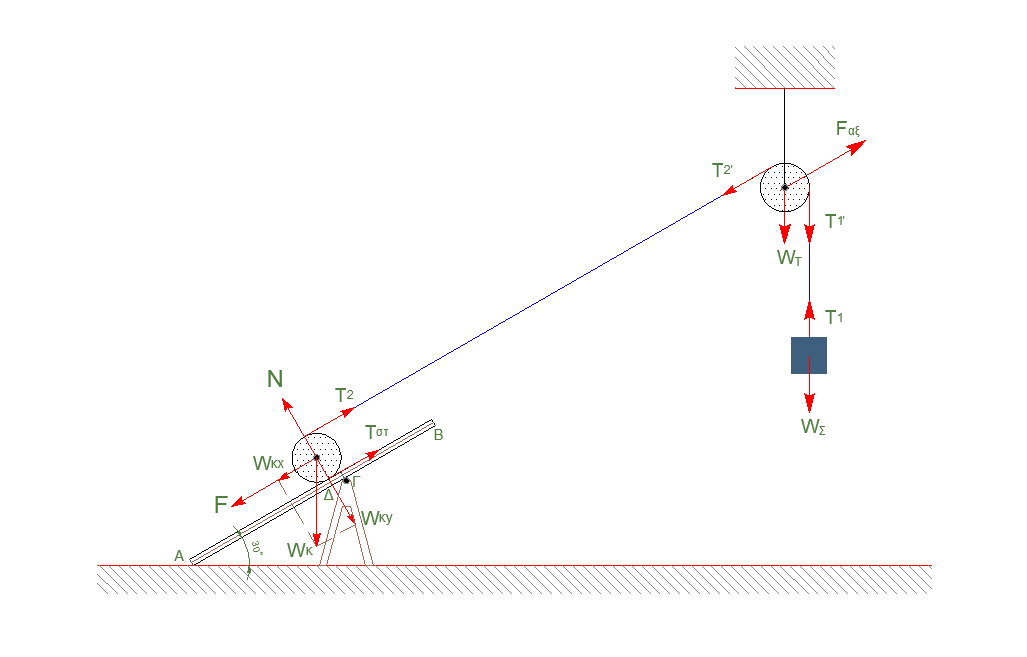
Δ1-\((4)\)
\[M_Σ, \quad ισορροπία, \Rightarrow Σ\vec{F} = 0\] \[T_1 = Μ_Σ \cdot g \Rightarrow T_1 = 20N\] \[M_T, \quad ισορροπία, \Rightarrow Σ\vecτ = 0\] \[T_1 \cdot R_T = T_2 \cdot R_T \Rightarrow T_2 = 20N\] \[α) \underline {τρόπος}\] \[M_K, \quad ισορροπία, \Rightarrow Σ\vecτ_{(K)} = 0\] \[T_2 \cdot R_K = T_{στ} \cdot R_Κ \Rightarrow T_2 = Τ_{στ}\] \[M_K, \quad ισορροπία, \Rightarrow Σ \vec{F} = 0\] \[T_2 + Τ_{στ} = F + Μ_Κ \cdot g \cdot ημφ \Rightarrow 2T_2 = F +10 \Rightarrow F = 30N\] \[β) \underline {τρόπος}\] \[M_K, \quad ισορροπία, \Rightarrow Σ\vecτ_{(Δ)} = 0\] \[T_2 \cdot 2 \cdot R_K = (F + Μ_Κ \cdot g \cdot ημφ) \cdot R_K \Rightarrow 40 = F +10 \Rightarrow F = 30N\]Δ2-\((8)\)
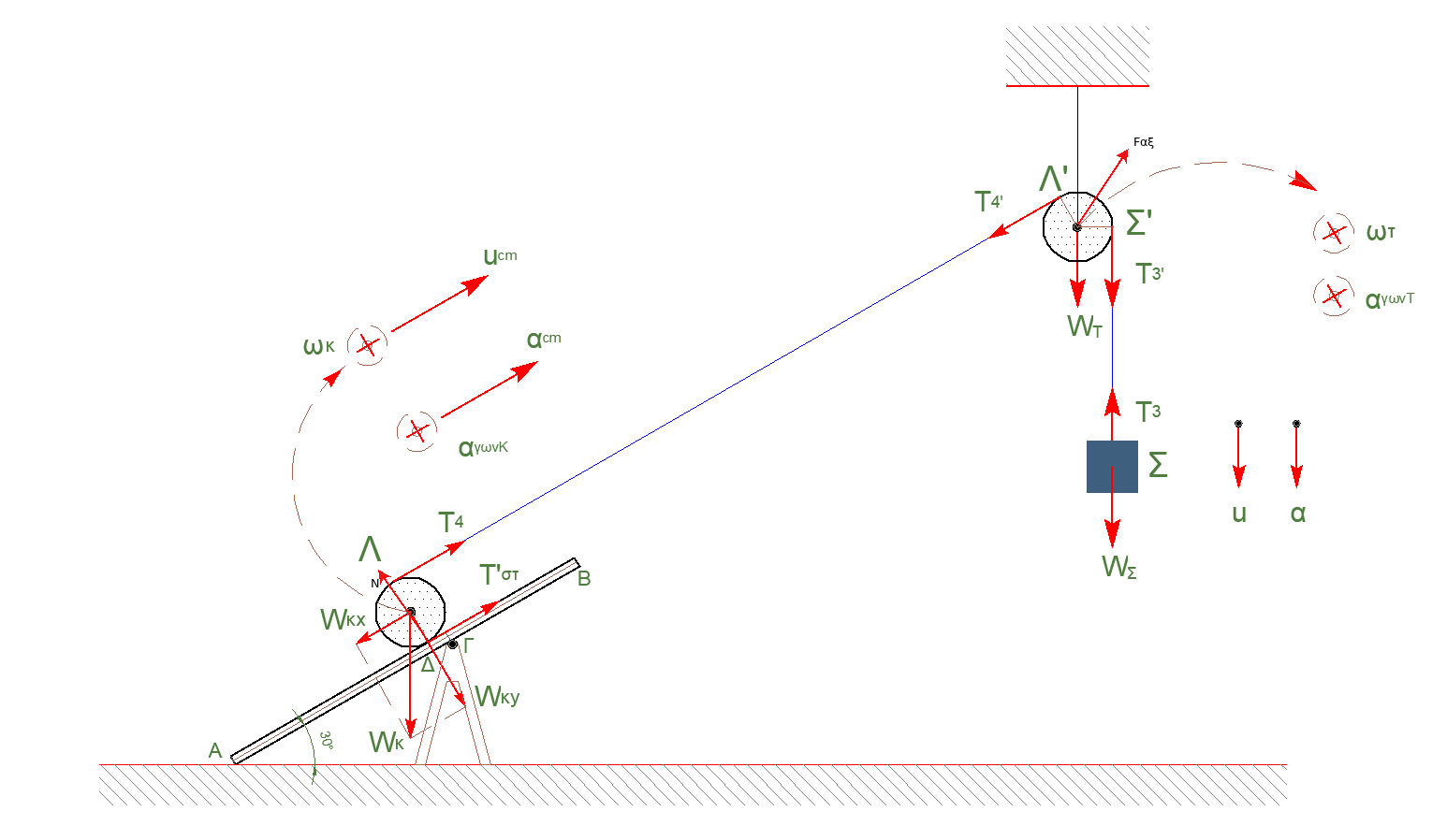
νήμα κατακόρυφο αβαρές, μη εκτατό
\[α_Σ = α_{Σ'} = α_{γρ} = α_{γων_Τ} \cdot R_T \Rightarrow α_Σ = α_{γων_Τ} \cdot R_T \quad (1)\]νήμα πλάγιο αβαρές, μη εκτατό
\[α_Λ = α_{Λ'} = α_{γρ} = α_{γων_Τ} \cdot R_T \Rightarrow α_Λ = α_{γων_Τ} \cdot R_T \quad (2)\]Κύλινδρος \(Κ.Χ.Ο.\)
\[υ_Α = 0 \Rightarrow υ_{cm} = ω \cdot R_K \Rightarrow α_{cm} = α_{γων_Κ} \cdot R_K \quad (3)\] \[υ_Λ = υ_{cm} + ω \cdot R_K \Rightarrow υ_Λ = 2 \cdot υ_{cm} \Rightarrow α_Λ = 2 \cdot α_{cm} \quad (4)\] \[M_Σ: \quad METΑΦΟΡΙΚΗ \Rightarrow Σ\vec{F} = M_Σ \cdot \vec{α_Σ}\] \[Μ_Σ \cdot g - T_3 = M_Σ \cdot α_Σ \Rightarrow 20 - T_3 = 2 \cdot α_Σ \quad (5)\] \[M_T: \quad ΣΤΡΟΦΙΚΗ \Rightarrow Σ\vecτ = Ι_T \cdot \vecα_{γων_Τ}\] \[T_3' \cdot R_T - T_4' \cdot R_T = \frac{1}{2} \cdot M_T \cdot R_T^2 \cdot α_{γων_T} \overset{(2)}{\implies} T_3 - T_4 = R_T \cdot α_{γων_Τ} \quad (6)\] \[α) \underline {τρόπος}\] \[M_Κ: \quad METΑΦΟΡΙΚΗ \Rightarrow Σ\vec{F} = Μ_Κ \cdot \vecα_{cm}\] \[T_4 + T_{στ} - Μ_Κ \cdot g \cdot ημφ = Μ_Κ \cdot α_{cm} \Rightarrow T_4 + T_{στ} - 10 = 2\cdot α_{cm} \quad (7)\] \[M_K: \quad ΣΤΡΟΦΙΚΗ \Rightarrow Σ\vecτ = Ι_K \cdot \vecα_{γων_K}\] \[T_4 \cdot R_K - T_{στ} \cdot R_Κ = \frac{1}{2} \cdot M_Κ \cdot R_Κ^2 \cdot α_{γων_Κ} \Rightarrow T_4 - T_{στ} = R_K \cdot α_{γων_Κ} \quad (8)\] \[β) \underline {τρόπος}\] \[Ι_{Κ(Δ)} = Ι_{cm} + M_Κ \cdot R_K^2 \Rightarrow Ι_{Κ(Δ)} = \frac{3}{2} \cdot M_K \cdot R_K^2 (7)\] \[M_K: \quad ΣΤΡΟΦΙΚΗ \Rightarrow Σ\vecτ = Ι_{K_Δ} \cdot \vecα_{γων_Δ}\] \[T_4 \cdot 2 \cdot R_K - M_Κ \cdot g \cdot ημφ \cdot R_Κ = \frac{3}{2} \cdot M_Κ \cdot R_Κ^2 \cdot α_{γων_Δ} \Rightarrow 2\cdot T_4 - 10 = 3 \cdot R_K \cdot α_{γων_Δ} \quad (8)\]Λύση του μη γραμμικού συστήματος των \(8\) εξισώσεων με τους \(10\) αγνώστους \(α_Σ = 4 \frac{m}{s^2}\)
Δ3-\((6)\)
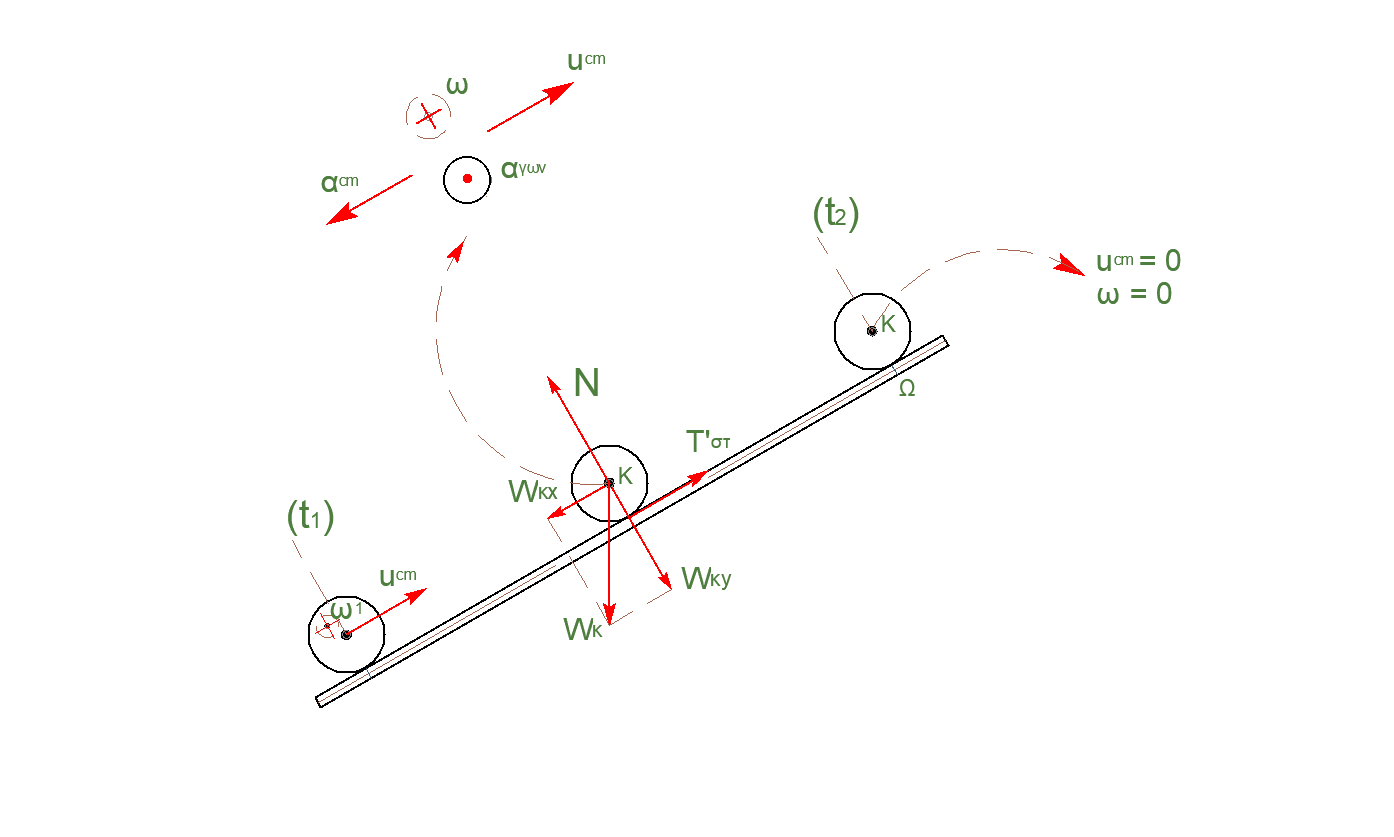
Δ4-\((3)\)
\[M_K: ΜΕΤΑΦΟΡΙΚΗ, \quad 0-t_1\] \[x_{cm1} = \frac{1}{2} \cdot α_{cm} \cdot t_1^2 \Rightarrow x_{cm1} = 0.25m\] \[α) \underline {τρόπος}\] \[M_K: ΜΕΤΑΦΟΡΙΚΗ, \quad t_1 - t_2\] \[Δx_{cm} = υ_{cm1} \cdot Δt - \frac{1}{2} \cdot α_{cm} \cdot Δt^2 \Rightarrow Δx_{cm} = 0.15m\] \[β) \underline {τρόπος}\]Από την λύση του μη γραμμικού συστήματος έχουμε
\[α_{cm} = 2 \frac{m}{s^2} \quad α_{γων_Κ} = \frac{2}{R_K}\] \[υ_{cm1} = α_{cm} \cdot t_1 \Rightarrow υ_{cm1} = 1 \frac{m}{s}\] \[ω_1 = α_{γων_Κ} \cdot t_1 \Rightarrow ω_1 = \frac{1}{R_Κ} \frac{rad}{s}\] \[ΑΔΜΕ_{t1 \rightarrow t_2}\] \[E_M^{t1} = E_M^{t2} \Rightarrow K_{στρ}^{t1} + K_{μετ}^{t1} + U^{t1} = K_{στρ}^{t2} + K_{μετ}^{t2} + U^{t2}\] \[\frac{1}{2} \cdot I \cdot ω_1^2 + \frac{1}{2} \cdot M_K \cdot υ_{cm}^2 +0 = 0+ 0+ M_K \cdot g \cdot h \Rightarrow h = 0.075m\] \[ημφ = \frac{h}{Δx_{cm}} \Rightarrow Δx_{cm} = 0.15m\] \[γ) \underline {τρόπος}\] \[ΘΜΚΕ_{(t_1 \rightarrow t_2)} \quad ΔΚ = ΣW\] \[K_{t_2} - Κ_{t_1} = W_B + W_{T_{στατ}} \Rightarrow 0 - \frac{1}{2} \cdot Μ_Κ \cdot υ_{cm1}^2 = -M_K \cdot g \cdot ημφ \cdot Δx_{cm} + T_{στατ} \cdot Δx_{cm} \Rightarrow Δx_{cm} = 0.15m\] \[x_{ολ} = x_{cm1} + Δx_{cm} \Rightarrow x_{ολ} = 0.4m\]Δ5-\((4)\)
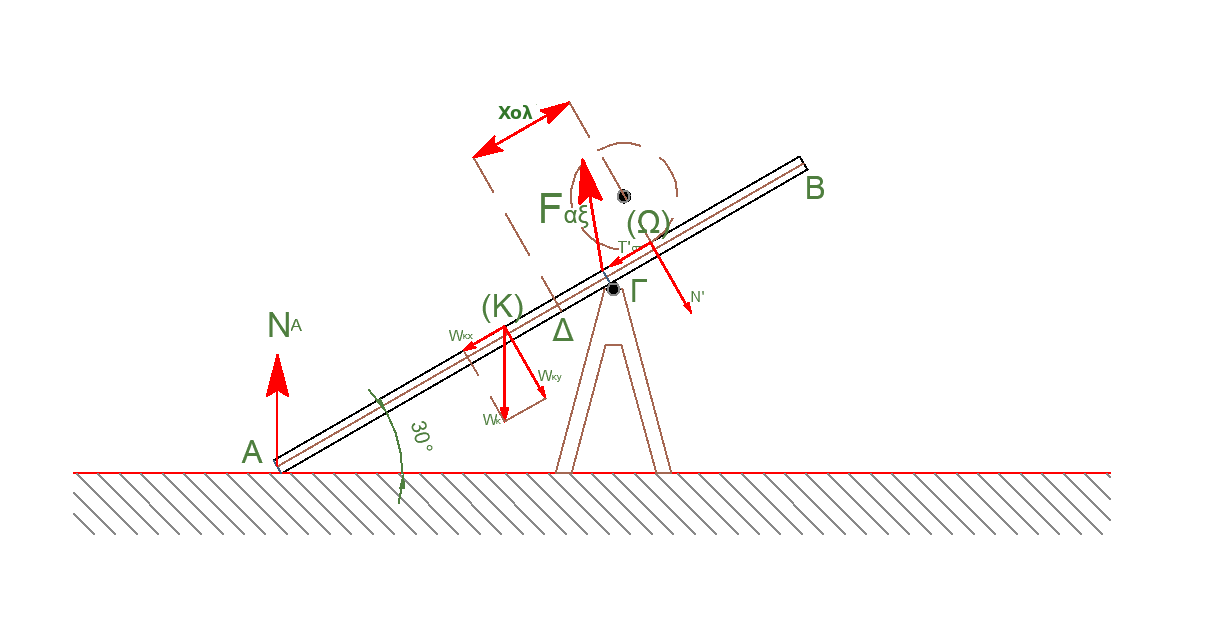
Θέλουμε να αποδείξουμε ότι κατά την διάρκεια της ανόδου του κυλίνδρου πάνω στην σανίδα από τη χρονική στιγμή \(t=0\) έως τη χρονική στιγμή \(t=t_2\), που ο κύλινδρος σταματάει στιγμιαία, η σανίδα δεν ανατρέπεται. Ο κύλινδρος ξεκινάει από τη θέση \(Δ (x=0)\) και κινείται με ευθύγραμμη ομαλά επιταχυνόμενη κίνηση από την χρονική στιγμή \(t=0\) έως τη χρονική στιγμή \(t=t_1\). Όσο κινείται κάτω από τη θέση \(Γ\) η σανίδα δεν μπορεί να ανατραπεί αφού και η ροπή του βάρους της σανίδας και η ροπή του βάρους του κυλίνδρου τείνουν να περιστρέψουν την σανίδα αριστερόστροφα.
\[x = \frac{1}{2} \cdot a \cdot t^2 \Rightarrow (ΔΓ) = \frac{1}{2} \cdot a_{cm} \cdot t_Γ^2 \Rightarrow t_Γ = \sqrt{0,2} \Rightarrow t_Γ = \frac{\sqrt5}{5} s\] \[t_Γ = \frac{\sqrt5}{5} \approx 0.447 < 0.5 s\] \[υ_Γ = a_{cm} \cdot t_Γ \Rightarrow υ_Γ = \frac{2 \cdot \sqrt5}{5} \frac{m}{s}\]Από την χρονική στιγμή \(t = t_Γ\) έως την χρονική στιγμή \(t=t_1\) θα αποδείξουμε ότι ισχύει
\[|τ_{W_Σ}| > |τ_{N'}|\]Όπου \(|τ_{W_Σ}|\) είναι το μέτρο της ροπής του βάρους της σανίδας και \(|τ_{N'}|\) είναι το μέτρο της ροπής της αντίδρασης του κυλίνδρου στην δράση \(Ν\) της σανίδας στον κύλινδρο. Θα χρησιμοποιήσουμε διπλές συνεπαγωγές
\[|τ_{W_Σ}| > |τ_{N'}| \iff Μ_ρ \cdot g \cdot συνφ \cdot (ΚΓ) > Μ_k \cdot g \cdot συνφ \cdot (x - x_Γ)\] \[(ΚΓ) > (x - x_Γ) \iff 0.5 > υ_Γ \cdot (t - t_Γ) + \frac{1}{2} \cdot a_{cm} \cdot (t - t_Γ)^2\]και μετά τις πράξεις φτάνουμε στην ανίσωση
\[t^2 < 0,7\]H ανίσωση αληθεύει για \(-\sqrt7 < t < \sqrt7\) άρα και για την χρονική διάρκεια από \(t = t_Γ = \frac{\sqrt5}{5} s\) έως \(t=t_1=0.5 s\)
Από την χρονική στιγμή \(t = t_1\) έως την χρονική στιγμή \(t=t_2\) που ο κύλινδρος κάνει ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση με επιβράδυνση \(a_{cm} = \frac{10}{3} \frac{m}{s^2}\) θα αποδείξουμε ότι ισχύει
\[|τ_{W_Σ}| > |τ_{N'}|\]Όπου \(|τ_{W_Σ}|\) είναι το μέτρο της ροπής του βάρους της σανίδας και \(|τ_{N'}|\) είναι το μέτρο της ροπής της αντίδρασης του κυλίνδρου στην δράση \(Ν\) της σανίδας στον κύλινδρο. Θα χρησιμοποιήσουμε διπλές συνεπαγωγές
\[|τ_{W_Σ}| > |τ_{N'}| \iff Μ_ρ \cdot g \cdot συνφ \cdot (ΚΓ) > Μ_k \cdot g \cdot συνφ \cdot (x - x_Γ)\] \[(ΚΓ) > (x - x_Γ) \iff 0.5 > x_1 + υ_{cm1} \cdot (t - t_1) - \frac{1}{2} \cdot a_{cm} \cdot (t - t_1)^2 -x_Γ\]και μετά τις πράξεις φτάνουμε στην ανίσωση
\[-5t^2 + 8 \cdot t - 4.1 < 0\]H ανίσωση αληθεύει για κάθε \(t \in \mathbb{R}\) αφού η διακρίνουσα είναι αρνητική άρα και για την χρονική διάρκεια από \(t = t_1 = 0.5 s\) έως \(t=t_2=0.8 s\)
\[β) \underline {τρόπος}\]Έστω τυχαία θέση του κυλίνδρου για την οποία το σημείο επαφής του κυλίνδρου με την σανίδα έχει απομάκρυνση \(x\) από την θέση \(Γ\) Η δύναμη \(Ν_Α\) είναι από το λείο δάπεδο, και η \(Ν'\) είναι η αντίδραση του κυλίνδρου στην δράση \(Ν\) της σανίδας στον κύλινδρο. Στον κάθετο στην σανίδα άξονα η συνισταμένη των δυνάμεων που ασκούνται στον κύλινδρο είναι μηδέν, οπότε
\[Ν’ = Μ_κ \cdot g \cdot συνφ\] \[Σ\vecτ_{(Γ)} = 0 \Rightarrow -τ_{Ν_Α} \cdot (AΓ) \cdot συνφ - Ν' \cdot x + W_ρ \cdot συνφ \cdot (ΚΓ) = 0\] \[-N_A \cdot 2.5 \frac{\sqrt3}{2} +20 \cdot \frac{\sqrt3}{2} \cdot \frac{1}{2} -20 \cdot \frac{\sqrt3}{2} \cdot x\] \[2.5 \cdot N_A = 10 - 20\cdot x \Rightarrow N_A = \frac{10-20\cdot x}{2.5}\]Για να μην χάνεται η επαφή πρέπει
\[N_Α \geqslant 0 \Rightarrow \frac{10-20\cdot x}{2.5} \geqslant 0 \Rightarrow -20\cdot x \geqslant -10 \Rightarrow x \leq 0.5 m\]δηλαδή για να μην ανατραπεί η σανίδα πρέπει ο κύλινδρος να φτάσει μέχρι \(0,5m\) δεξιά του σημείου \(Γ\).
Ο κύλινδρος την στιγμή \(t_2\) έχει βρεθεί στην θέση \(x = Δ_{x_{ολ}} – (ΔΓ)=0,2m\) οπότε η σανίδα στο δοσμένο χρονικό διάστημα δεν ανατρέπεται.
\[γ) \underline {τρόπος}\] \[(ΓΔ) = 0.2m, \quad (ΚΓ) = 0.5m, \quad (ΓΩ) = x_{ολ} - (ΓΔ) \Rightarrow (ΓΩ) = 0.2m\] \[|τ_{W_ρ}| = Μ_ρ \cdot g \cdot συνφ \cdot (ΚΓ) \Rightarrow |τ_{W_ρ}| = 5 \sqrt3 N \cdot m\] \[|τ_N'| = Μ_k \cdot g \cdot συνφ \cdot (ΓΩ) \Rightarrow |τ_N'| = 2 \sqrt3 N \cdot m\] \[|τ_{W_ρ}| > |τ_N'|\]άρα η σανίδα δεν ανατρέπεται.
\[δ) \underline {τρόπος}\]Την στιγμή που ανατρέπεται η σανίδα ισχύει οριακά \(Ν_Α=0\), όπου \(Ν_A\) η δύναμη του δαπέδου, N’ η δύναμη που ασκεί ο κύλινδρος κάθετα στην επιφάνεια της σανίδας και \(W_{K_y}\) η κάθετη συνιστώσα του βάρους της σανίδας και \(Ψ\) το σημείο στο οποίο αν τοποθετηθεί ο κύλινδρος η σανίδα οριακά θα ανατραπεί.
\[Σ\vecτ_{(Γ)} = 0 \Rightarrow N' \cdot (ΓΨ) - W_{K_y} \cdot (ΚΓ) = 0\] \[M_Κ \cdot g \cdot συνφ \cdot (ΩΓ) - Μ_ρ \cdot g \cdot συνφ \cdot (ΚΓ)\] \[2 \cdot 10 \cdot \frac{\sqrt3}{2} \cdot x - 2 \cdot 10 \cdot \frac{\sqrt3}{2} \cdot \frac{1}{2} \Rightarrow x = 0.5 m\]Δηλαδή το σημείο \(Ψ\) απέχει \(0.5m\) από την άρθρωση \(Γ\) και \(1m\) από το άκρο \(Β\) της σανίδας.
Άρα η θέση ανατροπής είναι σε \(x = 0.5 m\) από το σημείο \(Γ\). Όμως το σώμα φτάνει σε απόσταση \(l = 0.2 m\) πάνω από το \(Γ\). Αφού \(l < x\) η σανίδα δεν ανατρέπεται.
\[ε) \underline {τρόπος}\]Η “εις άτοπον απαγωγή”
Έστω ότι την χρονική στιγμή \(t_2\), δηλαδή την στιγμή που ο κύλινδρος σταματά στιγμιαία, η σανίδα ανατρέπεται. Αυτό σημαίνει ότι η σανίδα δεν είναι σε επαφή με το δάπεδο δηλαδή ισχύει \(Ν=0 \Rightarrow τ_Ν = 0\). Θεωρούμε θετική φορά για τις ροπές, αυτή των δεικτών του ρολογιού.
\[(ΓΔ) = 0.2m, \quad (ΚΓ) = 0.5m, \quad (ΓΩ) = x_{ολ} - (ΓΔ) \Rightarrow (ΓΩ) = 0.2m\] \[τ_{W_ρ} = - Μ_ρ \cdot g \cdot συνφ \cdot (ΚΓ) \Rightarrow τ_{W_ρ} = - 5 \sqrt3 N \cdot m\] \[τ_N' = Μ_k \cdot g \cdot συνφ \cdot (ΚΓ) \Rightarrow τ_N' = 2 \sqrt3 N \cdot m\] \[Στ_{(Γ)} = τ_N' + τ_{W_ρ} = 2 \sqrt3 - 5 \sqrt3 \Rightarrow Στ_{(Γ)} < 0\]Αυτό σημαίνει ότι η σανίδα θα περιστραφεί με φορά αντίθετη από αυτή την ρολογιών, δηλαδή θα έρθει σε επαφή με το δάπεδο άρα θα ασκεί δύναμη στο δάπεδο, άρα και το δάπεδο θα ασκεί δύναμη στην σανίδα, δηλαδή \(Ν>0\)
Άρα άτοπο. Υποθέσαμε στην αρχή ότι η σανίδα ανατρέπεται δηλαδή \(Ν=0\) και οδηγηθήκαμε στο ότι \(Ν>0\) άρα η αρχική μας υπόθεση είναι εσφαλμένη. Άρα η σανίδα δεν ανατρέπεται.
Μια λάθος λύση για το \(Δ5\) εδώ μετά το 29:30.
Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus