Επαναληπτικό Διαγώνισμα Φυσικής 2019 2o ΓΕΛ Καλαμαριάς, 27ο ΓΕΛ Τούμπας, ΓΕΛ Χαλάστρας, 1ο ΓΕΛ Αλεξανδρούπολης
ΘΕΜΑ Α Στις ερωτήσεις \(Α_1-Α_4\) να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και
δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την
ημιτελή πρόταση.
\(Α_1\) Άνθρωπος κινείται με ταχύτητα \(υ = 11 \frac{m}{s}\) κατά μήκος ευθείας οδού που ενώνει δύο σταθμούς που οι σειρήνες τους ηχούν ταυτόχρονα με συχνότητα \(f = 225Hz\). Η ταχύτητα του ήχου στον αέρα \(υ_{ηχ} = 330 \frac{m}{s}\). Η συχνότητα των διακροτημάτων τα οποία αντιλαμβάνεται ο άνθρωπος είναι:
- $$15 Hz$$
- $$\frac{1}{15} Hz$$
- $$3375 Hz$$
\(Α_2\) Στο σωλήνα του ακόλουθου σχήματος το ιδανικό υγρό ρέει από το σημείο \(Δ\) προς το σημείο \(Α\). Τα σημεία \(Α, Β, Γ\) και \(Δ\) βρίσκονται στην ίδια ρευματική γραμμή. Η διατομή του σωλήνα στα σημεία \(Γ\) και \(Δ\) είναι η ίδια ενώ αυτά παρουσιάζουν υψομετρική διαφορά \(h\). Οι πιέσεις του ιδανικού υγρού στα σημεία \(Α, Β, Γ,\) και \(Δ\) συνδέονται με τις σχέσεις
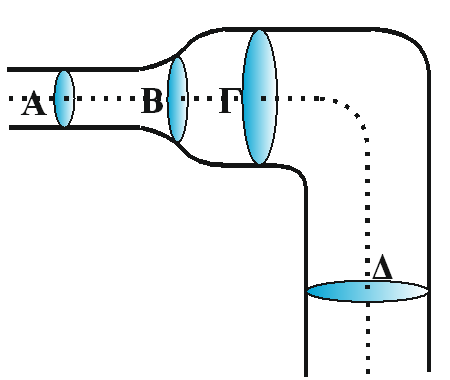
- $$p_A = p_B = p_Γ < p_Δ$$
- $$p_A > p_B > p_Γ > p_Δ$$
- $$p_A < p_B < p_Γ = p_Δ$$
- $$p_A < p_B < p_Γ < p_Δ$$
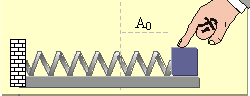
\(Α_3\) Εκτρέπουμε το σώμα του παρακάτω σχήματος κατά \(Α_0\) και τη χρονική στιγμή \(t = 0\) το αφήνουμε ελεύθερο. Αν στο σώμα ενεργεί δύναμη απόσβεσης \(F = - bυ\) τότε ο μέγιστος ρυθμός απώλειας ενέργειας θα εμφανιστεί τη χρονική στιγμή
- $$ \frac{T}{8} $$
- $$ \frac{T}{4} $$
- $$ \frac{T}{2} $$
- $$ T $$
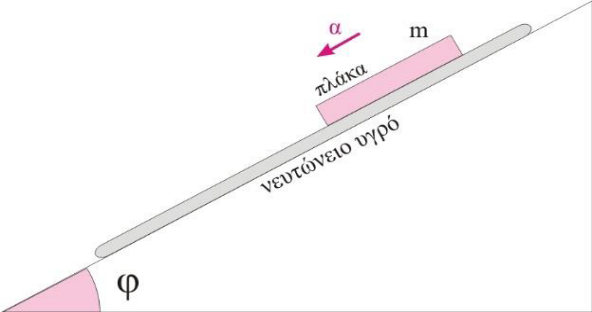
\(Α_4\) Μια πλάκα εμβαδού \(Α\) και μάζας \(m\) αφήνεται χωρίς αρχική ταχύτητα να κινηθεί πάνω στο πλάγιο επίπεδο του σχήματος γωνίας \(φ\). Μεταξύ της πλάκας και του επιπέδου υπάρχει στρώμα νευτώνειου υγρού πάχους \(d\) και συντελεστή ιξώδους \(n\). H πλάκα θα κινείται στο επίπεδο με επιτάχυνση της οποίας το μέτρο:
- παραμένει σταθερό.
- από μια μέγιστη τιμή μειώνεται μέχρι μηδενισμού του.
- από μια μέγιστη τιμή μειώνεται μέχρι να αποκτήσει μια σταθερή τιμή διάφορη του μηδενός.
- από μηδέν αυξάνεται μέχρι μια μέγιστη τιμή
\(Α_5\) Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.
- Το φαινόμενο Doppler χρησιμοποιείτα από τους γιατρούς, για τον προσδιορισμό της ροής του αίματος.
- Μια κρούση λέγεται έκκεντρη όταν οι ταχύτητες των κέντρων μάζας των σωμάτων που συγκρούονται είναι παράλληλες.
- Η ορμή ενός σώματος μεταβάλλεται εάν ασκηθεί πάνω του ζεύγος δυνάμεων.
- Από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων που γίνονται γύρω από το ίδιο σημείο και έχουν την ίδια διεύθυνση και συχνότητα, προκύπτει μια κίνηση που έχει σταθερό πλάτος που εξαρτάται από τα πλάτη και τη διαφορά φάσης των δύο επιμέρους ταλαντώσεων.
- Οι μονάδες της σταθεράς απόσβεσης σε μια φθίνουσα ταλάντωση είναι $$\frac{Νm}{s}$$
ΘΕΜΑ Β
\(Β_1\)
Κατά μήκος ευθείας \(x’x\) βρίσκονται στις θέσεις \(K\) και \(Λ\) δύο σημειακές πηγές \(Π_1\) και \(Π_2\) παραγωγής μηχανικών αρμονικών κυμάτων. Η εξίσωση που περιγράφει τις απομακρύνσεις τους από τη θέση ισορροπίας τους σε συνάρτηση με το χρόνο είναι \(y=A\cdot ημωt\). Η απόσταση \((ΚΛ)\) είναι \(6cm\). Το μήκος κύματος των παραγόμενων κυμάτων είναι \(4cm\). Σε σημείο \(Σ\) της ευθείας \(x’x\), το οποίο δεν ανήκει στο ευθύγραμμο τμήμα \(ΚΛ\) και δεν βρίσκεται κοντά στις πηγές, το πλάτος ταλάντωσής του \(|Α’|\) θα είναι:
- $$|A'| = 2A$$
- $$|A'| = 0$$
- $$0< |A'|<2A$$
Να επιλέξετε τη σωστή πρόταση και να δικαιολογήσετε την επιλογή σας.
\(Β_2\)
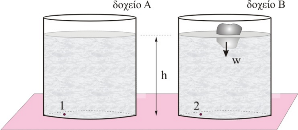
Τα δύο δοχεία \(Α\) και \(Β\) του σχήματος περιέχουν το ίδιο υγρό και στο δοχείο \(B\) επιπλέει ένα σώμα βάρους \(w\). Η ελεύθερη επιφάνεια του υγρού βρίσκεται στο ίδιο ύψος \(h\) και στα δύο δοχεία. Για τις ολικές πιέσεις στα σημεία \(1\) και \(2\) των πυθμένων των δύο δοχείων έχουμε
- $$p_1 = p_2$$
- $$p_1 > p_2$$
- $$p_1 < p_2$$
Να επιλέξετε τη σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.
\(Β_3\)
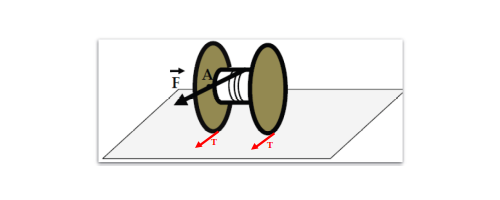
Στερεό αποτελείται από ομογενή κυλινδρικό φλοιό μάζας \(Μ\) και ακτίνας \(R\) και δύο όμοιους δίσκους μάζας \(2Μ\) και ακτίνας \(2R\) ο καθένας, που συνδέονται έτσι ώστε τα κέντρα μάζας όλων να βρίσκονται πάνω στον άξονα συμμετρίας του κυλίνδρου. Στον κύλινδρο όπως φαίνεται στο σχήμα είναι τυλιγμένο πολλές φορές αβαρές και μη εκτατό νήμα, που δεν ολισθαίνει πάνω στον κύλινδρο όταν ασκείται δύναμη στο ελεύθερο άκρο του \(A\). Το στερεό αρχικά ηρεμεί σε οριζόντιο δάπεδο. Ασκούμε στο ελεύθερο άκρο του νήματος \(A\) σταθερή οριζόντια δύναμη \(F\) και το στερεό κυλά χωρίς να ολισθαίνει σε οριζόντιο δάπεδο. Αν η ροπή αδράνειας του κυλινδρικού φλοιού είναι \(Ι_φ = Μ \cdot R^2\) και η ροπή αδράνειας κάθε κυκλικού δίσκου είναι \(Ι_δ = \frac{1}{2} \cdot m \cdot r^2\) τότε η επιτάχυνση του σημείου \(A\) είναι:
- $$\frac{9}{29} \cdot \frac{F}{M} $$
- $$\frac{6}{29} \cdot \frac{F}{M}$$
- $$\frac{3}{29} \cdot \frac{F}{M}$$
Να επιλέξετε τη σωστή πρόταση και να δικαιολογήσετε την επιλογή σας.
ΘΕΜΑ Γ
Δύο σύγχρονες πηγές \(Π_1\) και \(Π_2\) που απέχουν απόσταση \(d=8m\), παράγουν στην επιφάνεια ενός υγρού αρμονικά κύματα που έχουν ταχύτητα διάδοσης \(υ=20\frac{m}{s}\). Η εξίσωση της απομάκρυνσης των πηγών σε συνάρτηση με το χρόνο δίνεται από τη σχέση \(y=0,4ημ20πt\) (SI). Σε ένα σημείο \(Σ\) της επιφάνειας του υγρού που απέχει απόσταση \(r_1=5m\) από την πηγή \(Π_1\) και απόσταση \(r_2\) από την πηγή \(Π_2\) με \(r2 > r1\), τα δύο κύματα φτάνουν με χρονική διαφορά \(Δt=0,1s\).
\(Γ_1\) Να υπολογίσετε την απόσταση \(r_2\).
\(Γ_2\) Να γράψετε την χρονική εξίσωση του ρυθμού μεταβολής της απομάκρυνσης του σημείου \(Σ\) και να κάνετε την γραφική της παράσταση για \(0 \leq t \leq 0,45sec\)
\(Γ_3\) Πόσες υπερβολές απόσβεσης υπάρχουν μεταξύ της πηγής \(Π_2\) και της υπερβολής που διέρχεται από το σημείο \(Σ\). Να τις σχεδιάσετε ποιοτικά.
\(Γ_4\) Η τρίτη υπερβολή ενισχυτικής συμβολής δεξιά της υπερβολής που διέρχεται από το σημείο \(Σ\) τέμνει την ευθεία που διέρχεται από τις πηγές \(Π_1\) και \(Π_2\) στο σημείο \(K\). Να βρείτε τις αποστάσεις του σημείου \(K\) από τις πηγές.
ΘΕΜΑ Δ
Ομογενής δίσκος μάζας \(Μ = 4kg\) και ακτίνας \(r = 1m\), μπορεί να στρέφεται σε κατακόρυφο επίπεδο, γύρω από οριζόντιο άξονα χωρίς τριβές. Στην περιφέρεια του δίσκου και στη διεύθυνση μιας ακτίνας του στερεώνεται ομογενής ράβδος μήκους \(d = 2m\) και μάζας \(m_ρ = 12kg\). Το σύστημα των δύο σωμάτων \(Σ_1\) ηρεμεί οριζόντιο με τη βοήθεια κατακόρυφου νήματος που έχει όριο θραύσης \(Τ_{θρ} = 240Ν\) που είναι δεμένο στο ελεύθερο άκρο της ράβδου και του οριζόντιου άξονα που διέρχεται από το κέντρο \(Ο\) του δίσκου. (Όριο θραύσης είναι η ελάχιστη δύναμη που απαιτείται ώστε να σπάσει το νήμα).
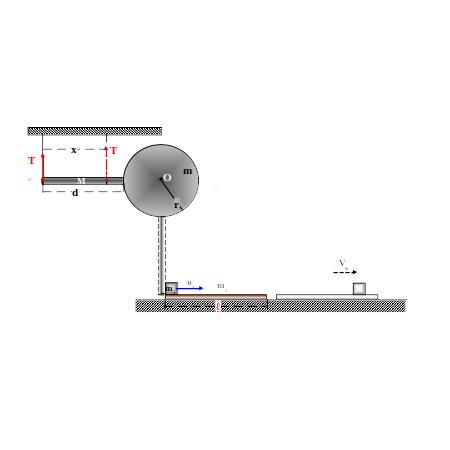
\(Δ_1\) Μετακινούμε οριζόντια το σημείο πρόσδεσης του νήματος στη ράβδο, ώστε το νήμα να διατηρείται κατακόρυφο. Να σχεδιάσετε το διάγραμμα της τάσης \(Τ\) του νήματος σε συνάρτηση με την οριζόντια απόσταση \(x\) του σημείου πρόσδεσης από το ελεύθερο άκρο της ράβδου μέχρι να κοπεί το νήμα.
\(Δ_2\) Καθώς μετακινούμε το νήμα, σε ορισμένη τιμή της απόστασης \(x\), αυτό κόβεται. Εκείνη τη στιγμή το στερεό \(Σ_1\) αρχίζει να στρέφεται γύρω από τον οριζόντιο άξονα που διέρχεται από το κέντρο \(Ο\) του δίσκου.
Να υπολογίσετε το ρυθμό μεταβολής της κινητικής ενέργειας του στερεού \(Σ_1\) τη στιγμή που η ράβδος σχηματίζει γωνία \(φ = \frac{π}{6} rad\) με την οριζόντια διεύθυνση.
\(Δ_3\) Τη χρονική στιγμή που η ράβδος γίνεται κατακόρυφη το στερεό \(Σ_1\) συγκρούεται με σώμα μάζας \(m_1 = 2kg\) που ηρεμεί πάνω σε οριζόντια σανίδα μάζας \(m_2 =4kg\) και μήκους \(ℓ\) αρκετού ώστε να μη χάνεται η επαφή μεταξύ τους. Η σανίδα ηρεμεί πάνω σε λείο οριζόντιο δάπεδο, ενώ ο συντελεστής τριβής σανίδας σώματος είναι \(μ = \frac{\sqrt5}{4}\). Μετά την κρούση το στερεό \(Σ_1\) συνεχίζει την περιστροφική του κίνηση χωρίς να αλλάξει φορά με γωνιακή ταχύτητα \(ω' = \sqrt5 \frac{r}{s}\). Να υπολογίσετε το επί τοις εκατό ποσοστό μεταβολής της κινητικής ενέργειας του συστήματος των σωμάτων στερεό \(Σ_1\) και σώμα μάζας \(m_1\) κατά την κρούση.
\(Δ_4\) Να βρεθεί ο ρυθμός μεταβολής της στροφορμής της ράβδου τη στιγμή που η ράβδος σχηματίζει γωνία \(θ = \frac{π}{6} rad\) με την κατακόρυφη διεύθυνση.
\(Δ_5\) Σε πόσο χρόνο από την στιγμή της κρούσης η σανίδα \(m_2\) και το σώμα \(m_1\) αποκτούν κοινή ταχύτητα.
Δίνονται: Η ροπή αδράνειας ομογενούς δίσκου ως προς άξονα που διέρχεται από το κέντρο του και είναι κάθετος στο επίπεδο του \(Ι_δ = \frac{1}{2} Mr^2\), η ροπή αδράνειας ομογενούς ράβδου μήκους \(d\) ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι κάθετος σε αυτή \(Ι_ρ = \frac{1}{12} Μd^2\), και η επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\).
blog comments powered by Disqus