Μοριοδότηση 2018
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(δ\)
Α3 - \(α\)
Α4 - \(δ\)
Α5: \(Λ - Σ - Λ - Σ - Λ\)
Θέμα Β
B1-\((i)\)
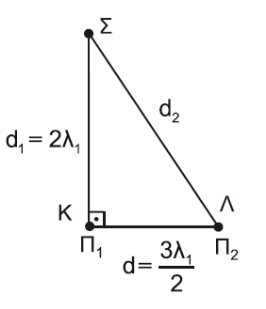
Ίδιο υλικό
\[υ_δ = λ_1 \cdot f_1 = λ_2 \cdot f_2 \overset{f_2=2\cdot f_1}{\implies} λ_2 = \frac{λ_1}{2}\] \[α) \underline {τρόπος}\] \[|A_Σ| = |2 A \cdot συν \frac{2π (d_1 - d_2)}{2 λ_2} | = |2 A \cdot συν \frac{π (2 λ_1 - \frac{5λ_1}{2} )}{\frac{λ_1}{2} }| = |2Α|\]άρα σωστό το \(i\)
\[β) \underline {τρόπος}\] \[\left. \begin{matrix}d_1 - d_2 = 2 λ_1 - \frac{5λ_1}{2} = - \frac{λ_1}{2} = -λ_2 \\\\ d_1 - d_2 = N \cdot λ_2\end{matrix} \right\} Ν = -1 \quad ενίσχυση\]άρα σωστό το \(i\)
\[γ) \underline {τρόπος}\]Από την πηγή \(Π_1\) το κύμα φτάνει στο σημείο \(Σ\) σε χρόνο \(t_1\)
\[t_1 = \frac{d_1}{υ} = \frac{2 \cdot λ_1}{υ} = 2Τ_1\]Από την πηγή \(Π_2\) το κύμα φτάνει στο σημείο \(Σ\) σε χρόνο \(t_2\)
\[t_2 = \frac{d_2}{υ} = \frac{5 \cdot \frac{λ_1}{2}}{υ} = \frac{5}{2} \cdot Τ_1\] \[f_2 = 2 \cdot f_1 \Rightarrow T_2 = \frac{T_1}{2}\]Τα κύματα από τις δύο πηγές φτάνουν στο σημείο \(Σ\) με χρονική διαφορά \(Δt\)
\[Δt = t_2 - t_1 = \frac{5}{2} \cdot Τ_1 - 2Τ_1 = \frac{T_1}{2} = T_2\]άρα σωστό το \(i\)
Β2 - \((ιιι)\)
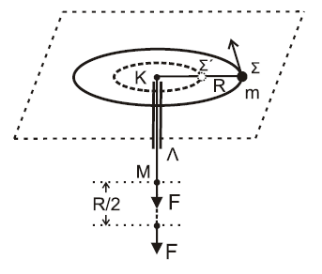
Η τάση του νήματος διέρχεται από τον άξονα περιστροφής
\[α) \underline {τρόπος}\] \[Άρα \quad m \cdot υ \cdot R = m \cdot υ´ \cdot \frac{R}{2} \Rightarrow υ´ = 2 υ\] \[ΘΜΚΕ_m (Σ \rightarrow Σ') \quad Κ_{Σ'} - Κ_{Σ} = W_F \Rightarrow \frac{1}{2} \cdot m \cdot υ´^2 - \frac{1}{2} \cdot m \cdot υ^2 = W_F\] \[\left. \begin{matrix} W_F = \frac{3}{2} \cdot m \cdot υ^2 \\\\ υ = ω \cdot R\end{matrix} \right\} W_F = \frac{3}{2} \cdot m \cdot ω^2 \cdot R^2\]άρα σωστό το \(iii\)
\[β) \underline {τρόπος}\] \[I_1 \cdot ω = Ι_2 \cdot ω´ \Rightarrow m \cdot R^2 \cdot ω = m \cdot \frac{R^2}{4} \cdot ω´ \Rightarrow ω´ = 4ω\] \[ΘΜΚΕ_m (Σ \rightarrow Σ') \quad Κ_{Σ'} - Κ_{Σ} = W_F \Rightarrow \frac{1}{2} \cdot Ι_2 \cdot ω´^2 - \frac{1}{2} \cdot Ι_1 \cdot ω^2 = W_F\] \[W_F = \frac{1}{2}m \frac{R^2}{4}16ω^2 - \frac{1}{2}m \cdot R^2 ω^2 \Rightarrow W_F = \frac{3}{2} \cdot m \cdot ω^2 \cdot R^2\]άρα σωστό το \(iii\)
\[γ) \underline {τρόπος}\] \[I_1 \cdot ω = Ι_2 \cdot ω´ \Rightarrow m \cdot R^2 \cdot ω = m \cdot r^2 \cdot ω´ \Rightarrow ω´ = \frac{R^2 \cdot ω}{r^2}\]Αρχή του συστήματος αναφοράς το σημείο \(Σ\) και θετική φορά προς το κέντρο του κύκλου \(Κ\).
Για μετατόπιση \(x\) η ακτίνα του κύκλου είναι \(r = R - x\)
\[ω´ = \frac{R^2 \cdot ω}{(R-x)^2}\]Για την νέα θέση \(r = R - x\)
\[Τ = F = \frac{m \cdot υ´^2}{r} = m \cdot ω´^2 \cdot r = m \cdot (\frac{R^2 \cdot ω}{(R-x)^2})^2 \cdot (R-x)\] \[F = \frac{m \cdot ω^2 \cdot R^4}{(R-x)^3}\] \[W_F = \displaystyle\int_0^{\frac{R}{2}} F dx = \int_0^{\frac{R}{2}} \frac{m \cdot ω^2 \cdot R^4}{(R-x)^3} dx = - \int_0^{\frac{R}{2}} \frac{m \cdot ω^2 \cdot R^4}{(R-x)^3} d(R-x) = - m \cdot ω^2 \cdot R^4 \cdot \int_0^{\frac{R}{2}} \frac{d(R-x)}{(R-x)^3}\] \[W_F = - m \cdot ω^2 \cdot R^4 \cdot \frac{(R-x)^{-2}}{-2} \Bigg]_0^{\frac{R}{2}} = \frac{m \cdot ω^2 \cdot R^4}{2} \Bigg[\frac{1}{(R-x)^2} \Bigg]_0^{\frac{R}{2}}\] \[W_F = \frac{m \cdot ω^2 \cdot R^4}{2} \cdot \Bigg[ \frac{1}{(\frac{R}{2})^2} - \frac{1}{R^2} \Bigg] = \frac{m \cdot ω^2 \cdot R^4}{2} \cdot \Bigg[ \frac{4}{R^2} - \frac{1}{R^2} \Bigg]\] \[W_F = \frac{3}{2} \cdot m \cdot ω^2 \cdot R^2\]άρα σωστό το \(iii\)
H λάθος λύση.
Η δύναμη \(F\) σχεδιάζεται στο σχήμα στις δύο θέσεις με το ίδιο σύμβολο. Το μέγεθος του διανύσματος που χρησιμοποιείται είναι το ίδιο στην πρώτη και στην δεύτερη θέση οπότε σύμφωνα με την διατύπωση της άσκησης για κατάλληλη δύναμη “θεωρώ” το μέτρο της δύναμης σταθερό.
\[W = F \cdot x \Rightarrow W = F \cdot \frac{R}{2} \Rightarrow W = m \cdot \frac{υ^2}{R} \cdot \frac{R}{2}\]και μετά τις πράξεις κάνοντας και αντικατάσταση την σχέση
\[υ = ω \cdot R\] \[W = \frac{1}{2} \cdot m \cdot ω^2 \cdot R^2\]άρα σωστό το \(ι\)
Β3 - \((ι)\)
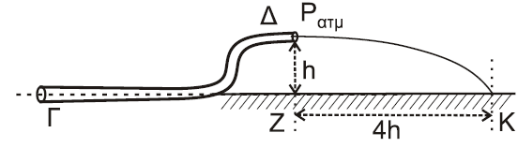
Εξίσωση Bernoulli για μια ρευματική γραμμή \((Γ \rightarrow Δ)\)
\[P_Γ + \frac{1}{2}ρ \cdot υ_Γ^2 = P_Δ + \frac{1}{2}ρ \cdot υ_Δ^2 + ρ \cdot g \cdot h\]Εξίσωση συνέχειας \((Γ \rightarrow Δ)\)
\[Π_Γ = Π_Δ \Rightarrow Α_Γ \cdot υ_Γ = Α_Δ \cdot υ_Δ \overset{Α_Γ = 2Α_Δ}{\implies} υ_Δ = 2υ_Γ\]Οριζόντια βολή \((Δ \rightarrow Κ)\)
\[\left. \begin{matrix} h = \frac{1}{2} g \cdot t^2 \\\\ 4h = υ_Δ \cdot t\end{matrix} \right\} 4h = υ_Δ \cdot \sqrt{\frac{2h}{g}} \Rightarrow υ_Δ^2 = 8g\cdot h \overset{υ_Δ = 2υ_Γ}{\implies} 4υ_Γ^2 = 8g\cdot h \Rightarrow υ_Γ^2 = 2g \cdot h\] \[g\cdot h = \frac{υ_Γ^2}{2}\]Άρα η εξίσωση Bernoulli γράφεται
\[P_Γ - P_Δ = \frac{1}{2}ρ \cdot υ_Δ^2 + ρ \cdot g \cdot h - \frac{1}{2}ρ \cdot υ_Γ^2 = \frac{1}{2}ρ \cdot 4 υ_Γ^2 + ρ \cdot \frac{υ_Γ^2}{2} - \frac{1}{2}ρ \cdot υ_Γ^2 = 2 ρ \cdot υ_Γ^2\]άρα σωστό το \(i\)
\[β) \underline {τρόπος - λάθος}\]Εξίσωση συνέχειας \((Γ \rightarrow Δ)\)
\[Π_Γ = Π_Δ \Rightarrow Α_Γ \cdot υ_Γ = Α_Δ \cdot υ_Δ \overset{Α_Γ = 2Α_Δ}{\implies} υ_Δ = 2υ_Γ\]Εξίσωση Bernoulli για μια ρευματική γραμμή \((Γ \rightarrow Δ)\)
\[P_Γ + \frac{1}{2}ρ \cdot υ_Γ^2 = P_Δ + \frac{1}{2}ρ \cdot υ_Δ^2 + ρ \cdot g \cdot h\] \[P_Γ - P_Δ = \frac{1}{2}ρ \cdot υ_Δ^2 + ρ \cdot g \cdot h - \frac{1}{2}ρ \cdot υ_Γ^2\] \[\overset{υ_Δ = 2υ_Γ}{\implies} ΔP = \frac{3}{2}ρ \cdot υ_Γ^2 + ρ \cdot g \cdot h\]Ισχύει ότι \(ρ \cdot g \cdot h > 0\)
Η επιλογή \(ii\) απορρίπτεται διότι \(\frac{3}{2}ρ \cdot υ_Γ^2 > ρ \cdot υ_Γ^2\)
Η επιλογή \(iii\) απορρίπτεται διότι \(\frac{3}{2}ρ \cdot υ_Γ^2 > \frac{1}{2} ρ \cdot υ_Γ^2\)
άρα σωστό το \(i\)
\[γ) \underline {τρόπος}\]Εξίσωση συνέχειας \((Γ \rightarrow Δ)\)
\[Π_Γ = Π_Δ \Rightarrow Α_Γ \cdot υ_Γ = Α_Δ \cdot υ_Δ \overset{Α_Γ = 2Α_Δ}{\implies} υ_Δ = 2υ_Γ\]Εξίσωση Bernoulli για μια ρευματική γραμμή \((Γ \rightarrow Κ)\)
\[P_Γ + \frac{1}{2}ρ \cdot υ_Γ^2 = P_Κ + \frac{1}{2}ρ \cdot υ_Κ^2\] \[P_K = P_Δ = P_{atm}\] \[P_Γ - P_Δ = \frac{1}{2}ρ \cdot (υ_Κ^2 - υ_Γ^2)\] \[h = \frac{1}{2} \cdot g \cdot t^2 \Rightarrow h = \frac{1}{2} \cdot g \cdot t \cdot t \Rightarrow h = \frac{1}{2} \cdot υ_{k_y} \cdot t \Rightarrow\] \[4h = υ_Δ \cdot t \Rightarrow 4 \cdot \frac{1}{2} \cdot υ_{k_y} \cdot t = υ_Δ \cdot t \Rightarrow υ_{k_y} = \frac{υ_Δ}{2}\] \[υ_Κ^2 = υ_{k_x}^2 + υ_{k_y}^2 \Rightarrow υ_Κ^2 = υ_Δ^2 + (\frac{υ_Δ}{2})^2 \Rightarrow υ_Κ^2 = \frac{5}{4} \cdot υ_Δ^2\] \[P_Γ - P_Δ = \frac{1}{2}ρ \cdot (υ_Κ^2 - υ_Γ^2) \Rightarrow P_Γ - P_Δ = \frac{1}{2}ρ \cdot (\frac{5}{4} \cdot υ_Δ^2 - υ_Γ^2) \Rightarrow P_Γ - P_Δ = 2 \cdot ρ \cdot υ_Γ^2\]άρα σωστό το \(i\)
Θέμα Γ
Γ1
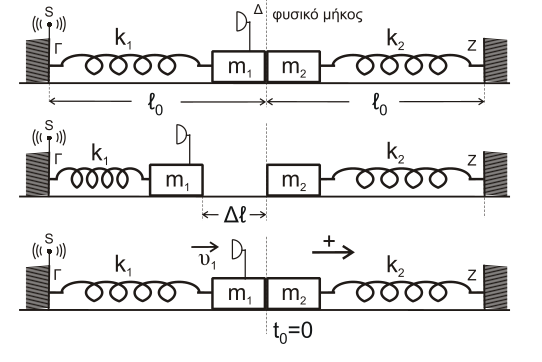
Γ2
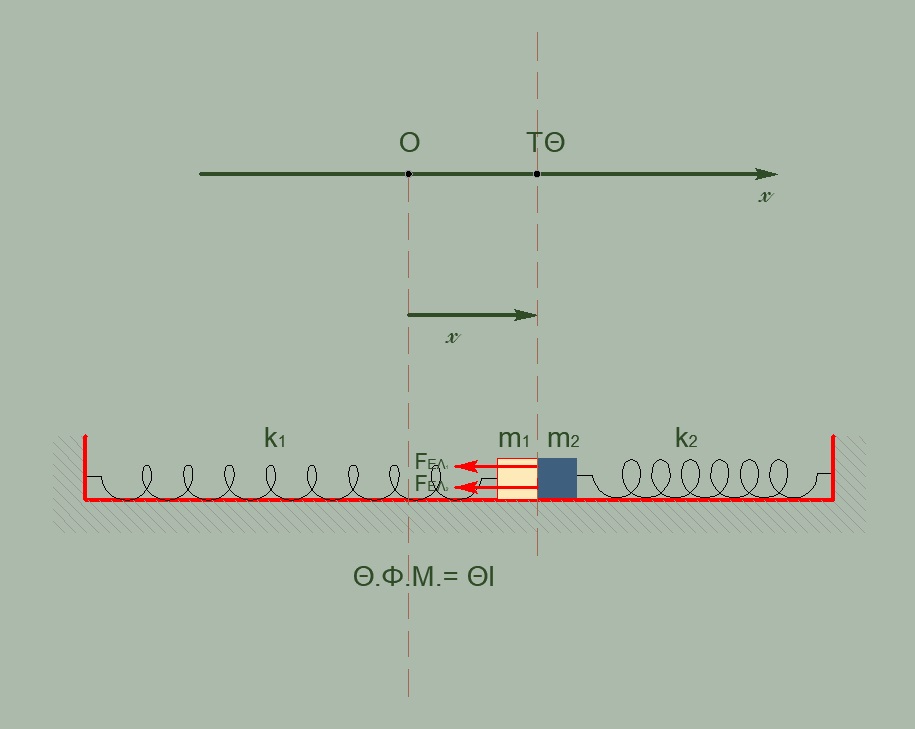
Στη θέση Θ.Φ.Μ. \(ΣF=0\) άρα αυτή είναι και Θ.Ι.
\[Τ.Θ.: ΣF = -F_{ΕΛ1} - F_{ΕΛ2} = -k_1 \cdot x - k_2 \cdot x = - (2k)x\]Για να εκτελεί ένα σώμα ΑΑΤ πρέπει να ισχύει
\[ΣF = -D \cdot x, D = 2k = (m_1 + m_2) ω^2 \Rightarrow ω = \sqrt{\frac{2k}{2m}} = \sqrt{\frac{k}{m}} = 5 \frac{rad}{sec}\] \[Θ.Ι.: V = υ_{max} \overset{υ_{max} = ω \cdot A}{\implies} 1 = 5 \cdot A \Rightarrow A = 0.2m\]Γ3
\[\left. \begin{matrix} f_{ΔΕΚΤΗ} = f_s \\\\ f_{ΔΕΚΤΗ} = \frac{υ_{ηχ} \pm υ_{ΣΥΣ}}{υ_{ηχ}} \cdot f_s\end{matrix} \right\} υ_{ΣΥΣ} = 0\]Για πρώτη φορά, δηλαδή ακραία θέση, οπότε
\[T = \frac{2π}{ω}= \frac{2π}{5} sec\] \[Δt = \frac{T}{4} = \frac{π}{10} sec\]Γ4
\[|\frac{dp}{dt}|_{m_1+m_2(max)} = ΣF_{max} = D \cdot A \overset{D = 100 \frac{N}{m}}{\implies} ΣF_{max}=20N, \quad ή \quad \frac{kg \cdot m}{sec^2}\]Θέμα Δ
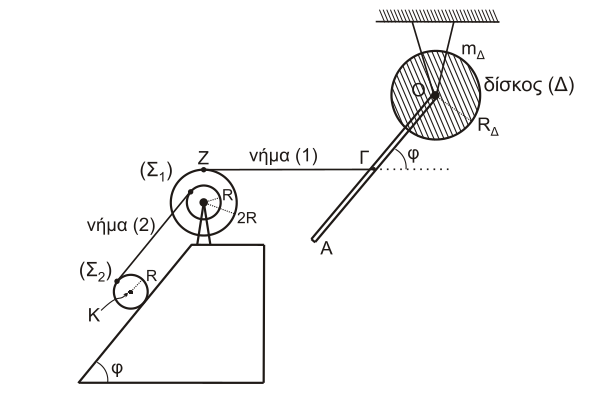
Ράβδος (ρ)
\[Μ = 8kg\] \[l = 3m\]Δίσκος (Δ)
\[m_Δ = 4kg\] \[R_Δ = \frac{\sqrt{2}}{2} m\]Τροχαλία (τροχ)
\[R = 0.2 m\] \[I_{τροχ} = 1.95 kg \cdot m^2\]Κύλινδρος
\[m = 30 kg\] \[R = 0.2 m\] \[ημφ = 0.8\] \[συνφ = 0.6\] \[g = 10 \frac{m}{sec^2}\]Δ1
\[I_{ρ-Δ} = (\frac{1}{12} \cdot M \cdot l^2 + M \frac{l^2}{4}) + \frac{1}{2} \cdot m_Δ \cdot R_Δ^2 = 25 kg \cdot m^2\]Δ2
\[|\frac{dL}{dt}|_{ρ-Δ} = Στ_{(0)} = W_ρ \cdot \frac{l}{2} \cdot συνφ = 72 \frac{kg \cdot m^2}{sec^2} \quad ή \quad N \cdot m\]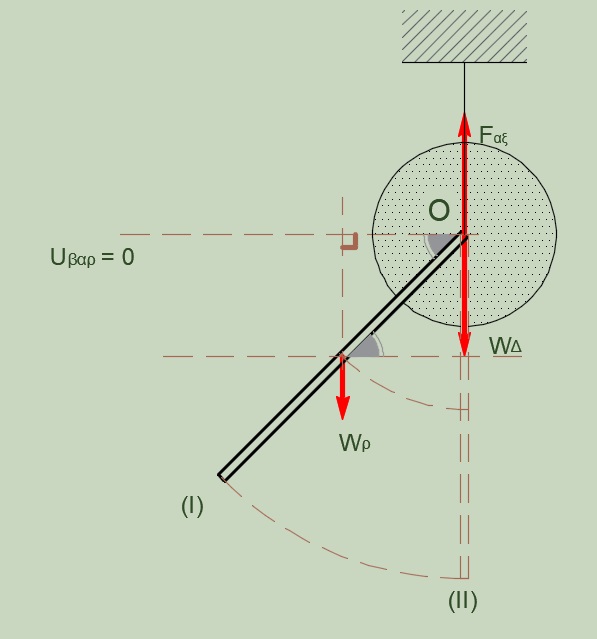
Δ3
\[α) \underline {τρόπος}\] \[ΑΔΜΕ_{ρ-Δ} (Ι \rightarrow II): K_I + U_1 = K_{II} + U_{II}\] \[0 + (-M \cdot g \cdot \frac{l}{2} \cdot ημφ + U_{βαρ(Δ)(Ι))}) = Κ_{ΙΙ} + (-Μ \cdot g \cdot \frac{l}{2} + U_{βαρ(Δ)(ΙI))})\] \[K_{II} = M \cdot g \cdot \frac{l}{2} \cdot (1 - ημφ) \Rightarrow K_{II} = 24J\] \[β) \underline {τρόπος}\]Επίπεδο μηδενικής δυναμικής ενέργειας βαρύτητας το άκρο της ράβδου την στιγμή που γίνεται κατακόρυφη.
\[ΑΔΜΕ_{ρ-Δ} (Ι \rightarrow II): K_I + U_1 = K_{II} + U_{II}\] \[0 + (M \cdot g \cdot (l - \frac{l}{2} \cdot ημφ) + U_{βαρ(Δ)(Ι))}) = Κ_{ΙΙ} + (Μ \cdot g \cdot \frac{l}{2} + U_{βαρ(Δ)(ΙI))})\] \[K_{II} = M \cdot g \cdot \frac{l}{2} \cdot (1 - ημφ) \Rightarrow K_{II} = 24J\] \[γ) \underline {τρόπος}\]Εύρεση του κέντρου μάζας του συστήματος των δύο σωμάτων (ράβδος, δίσκος)
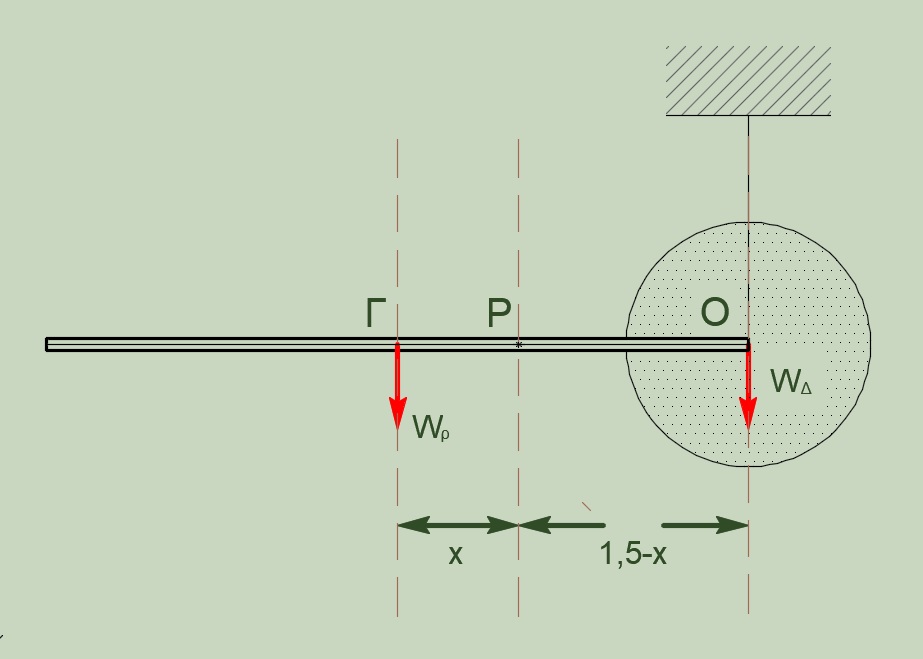
Έστω ότι το κέντρο μάζας \(Ρ\) του συστήματος απέχει απόσταση \(x\) από το μέσον \(Γ\) της ράβδου. Είναι προφανές ότι αν το σύστημα στηριχθεί στο κέντρο μάζας \(Ρ\) θα ισορροπήσει. Άρα
\[Στ_{Ρ} = 0 \Rightarrow τ_{W_Ρ} - τ_{W_Δ} = 0 \Rightarrow M \cdot g \cdot x = m_Δ \cdot g (\frac{l}{2} - x)\] \[8x = 4(1.5 - x) \Rightarrow x = 0.5 m \Rightarrow ΟΡ = 1m\]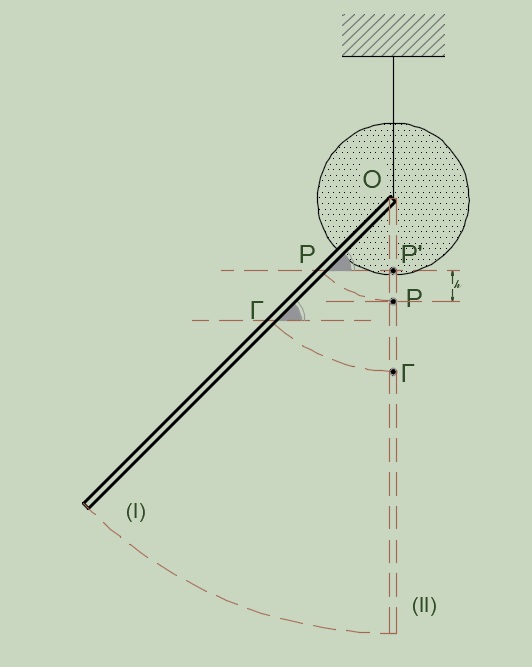
Επίπεδο μηδενικής δυναμικής ενέργειας βαρύτητας το κέντρο μάζας \(Ρ\) του συστήματος (ράβδου, δίσκου) την στιγμή που η ράβδος γίνεται κατακόρυφη.
\[ΑΔΜΕ_{ρ-Δ} (Ι \rightarrow II): K_I + U_1 = K_{II} + U_{II}\] \[0 + (M + m_Δ) \cdot g \cdot h = K_{II} \Rightarrow K_{II} = 24J\]Δ4
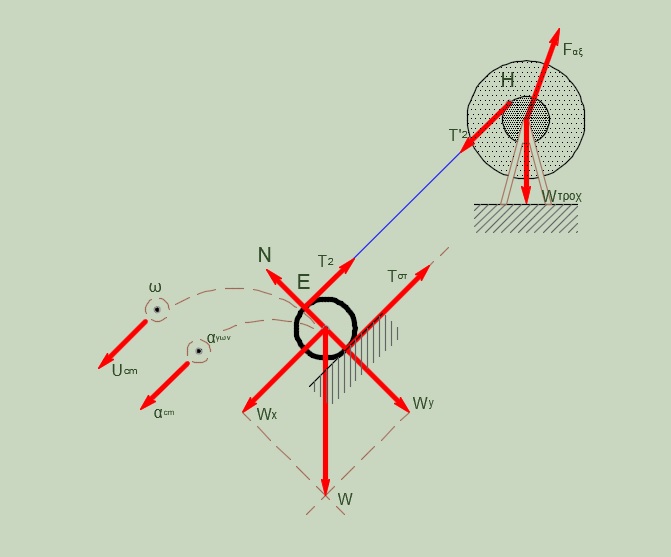
νήμα(2) αβαρές, μη εκτατό \((Τ_2 = Τ'_2)\)
ΚΧΟ:
\[υ_E = 2 \cdot υ_{cm} = 2 \cdot ω \cdot R \Rightarrow α_E = 2 \cdot α_{cm} = 2 \cdot α_{γων} \cdot R\] \[υ_E = υ_{H} = ω_{τροχ} \cdot R \Rightarrow α_E = α_{Η} = α_{γων_{τροχ}} \cdot R\]m: MET.
\[ΣF_x = m \cdot α_x \Rightarrow W_x - T_{στ} - Τ_2 = m \cdot α_{cm} \quad (1)\]m: ΣΤΡΟΦ.
\[Στ = Ι \cdot α_{γων} \Rightarrow T_{στ} \cdot R - T_2 \cdot R = \frac{1}{2} \cdot m \cdot R^2 \cdot α_{γων} \overset{α_{cm} = α_{γων} \cdot R}{\implies} T_{στ} - Τ_2 = \frac{1}{2} \cdot m \cdot α_{cm} \quad (2)\] \[(1)Λ(2) \Rightarrow W_x - 2T_2 = \frac{3}{2} \cdot m \cdot α_{cm} \quad (3)\] \[τροχ: \quad Στ = Ι \cdot α_{γων} \Rightarrow T'_2 \cdot R = 1.95 \cdot α_{γων(τροχ)} \overset{α_{γων(τροχ)} = \frac{2 α_{cm}}{R}}{\underset{(3)}{\implies}}\] \[W_x - 2 \cdot \frac{1.95 \cdot \frac{2 α_{cm}}{R}}{R} = \frac{3}{2} \cdot m \cdot α_{cm}\] \[300 \cdot 0.8 - \frac{4 \cdot 1.95 \cdot α_{cm}}{4 \cdot 10^{-2}} = 45 \cdot α_{cm} \Rightarrow α_{cm} = 1 \frac{m}{sec^2}\] \[α_{cm} = α_{γων} \cdot R \Rightarrow α_{γων} = 5 \frac{rad}{sec^2}\]κύλινδρος:
\[s = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow t = 2 sec\] \[υ_{cm} = α_{cm} \cdot t \Rightarrow υ_{cm} = 2 \frac{m}{sec}\] \[β) \underline {τρόπος}\]κύλινδρος:
\[ΘΜΚΕ_{Ο \rightarrow S}: K_{τελ} - Κ_{αρχ} = ΣW \Rightarrow (\frac{1}{2} \cdot m \cdot υ_{cm}^2 + \frac{1}{2} \cdot \frac{1}{2} \cdot m \cdot R^2 \cdot ω^2) -0 = (ΣF_x) \cdot S + (Στ) \cdot Δθ\] \[ΣF_x = m \cdot α_{cm}\] \[Στ = Ι \cdot α_{γων}\] \[\frac{3}{4} \cdot m \cdot υ_{cm}^2 = m \cdot α_{cm} \cdot s + \frac{1}{2} \cdot m \cdot R^2 \cdot α_{γων} \cdot Δθ \overset{α_{γων} \cdot R = α_{cm}}{\underset{Δθ \cdot R = S}{\implies}} \\\\] \[\frac{3}{4} \cdot m \cdot υ_{cm}^2 = m \cdot α_{cm} \cdot s + \frac{1}{2} \cdot m \cdot α_{cm} \cdot s \Rightarrow \frac{3}{4} \cdot m \cdot υ_{cm}^2 = \frac{3}{2} \cdot m \cdot α_{cm} \cdot S \Rightarrow υ_{cm} = 2 \frac{m}{sec}\] \[υ_{cm} = α_{cm} \cdot t \Rightarrow 2 = α_{cm} \cdot t \Rightarrow t = \frac{2}{α_{cm}}\] \[s = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow 2 = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow 2 = \frac{1}{2} \cdot α_{cm} \cdot (\frac{2}{α_{cm}})^2 \Rightarrow α_{cm} = 1 \frac{m}{s^2}\] \[γ) \underline {τρόπος}\]Ο κύλινδρος εκτελεί σύνθετη κίνηση, μεταφορική \(ΔS_{cm}\) και στροφική \(R \cdot Δθ\)
KXO για τον κύλινδρο
\[ΔS_{cm} = R \cdot Δθ\]Η στροφή της τροχαλίας κατά \(Δθ'\) έχει σαν αποτέλεσμα να ξετυλίγεται νήμα μήκους \(R \cdot Δθ'\).
\[R \cdot Δθ' = ΔS_{cm} + R \cdot Δθ\] \[R \cdot Δθ' = R \cdot Δθ + R \cdot Δθ \Rightarrow Δθ´ = 2 Δθ \Rightarrow \frac{dθ´}{dt} = 2 \cdot \frac{dθ}{dt} \Rightarrow ω´ = 2 \cdot ω\]Για το σύστημα των σωμάτων κύλινδρος - τροχαλία.
\[ΘΜΚΕ_{Ο \rightarrow S}: K_{τελ} - Κ_{αρχ} = ΣW \Rightarrow \frac{1}{2} \cdot m \cdot υ_{cm}^2 + \frac{1}{2} \cdot ( \frac{1}{2} \cdot m \cdot R^2) \cdot ω^2 + \frac{1}{2} \cdot Ι_{τροχ} \cdot (2 \cdot ω)^2 = m \cdot g \cdot ημφ \cdot s\]όπου \(ω = \frac{υ_{cm}}{R}\)
και μετά τις πράξεις \(υ_{cm} = 2 \frac{m}{s}\)
\[υ_{cm} = α_{cm} \cdot t \Rightarrow 2 = α_{cm} \cdot t \Rightarrow t = \frac{2}{α_{cm}}\] \[s = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow 2 = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow 2 = \frac{1}{2} \cdot α_{cm} \cdot (\frac{2}{α_{cm}})^2 \Rightarrow α_{cm} = 1 \frac{m}{s^2}\] \[δ) \underline {τρόπος}\]νήμα(2) αβαρές, μη εκτατό \((Τ_2 = Τ'_2)\)
ΚΧΟ:
\[υ_E = 2 \cdot υ_{cm} = 2 \cdot ω \cdot R\] \[υ_Η = υ_Ε \Rightarrow ω_{τροχ} \cdot R = 2 \cdot ω \cdot R \Rightarrow ω_{τροχ} = 2 \cdot ω\]ΑΔΕ:
\[U_{κυλ} = Κ_{μετ}^{κυλ} + Κ_{περ}^{κυλ} + Κ_{περ}^{τροχ} \Rightarrow m \cdot g \cdot h = \frac{1}{2} \cdot m \cdot υ_{cm}^2 + \frac{1}{2} \cdot I_{κυλ} \cdot ω^2 + \frac{1}{2} \cdot I_{τροχ} \cdot ω_{τροχ}^2\] \[m \cdot g \cdot s \cdot ημφ = \frac{1}{2} \cdot m \cdot υ_{cm}^2 + \frac{1}{2} \cdot ( \frac{1}{2} \cdot m \cdot R^2) \cdot ω^2 + \frac{1}{2} \cdot Ι_{τροχ} \cdot (2 \cdot ω)^2\]όπου \(ω = \frac{υ_{cm}}{R}\)
και μετά τις πράξεις \(υ_{cm} = 2 \frac{m}{s}\)
\[υ_{cm} = α_{cm} \cdot t \Rightarrow 2 = α_{cm} \cdot t \Rightarrow t = \frac{2}{α_{cm}}\] \[s = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow 2 = \frac{1}{2} \cdot α_{cm} \cdot t^2 \Rightarrow 2 = \frac{1}{2} \cdot α_{cm} \cdot (\frac{2}{α_{cm}})^2 \Rightarrow α_{cm} = 1 \frac{m}{s^2}\]Μπορείτε να εκτυπώσετε τις λύσεις σε μορφή pdf από εδώ και τα θέματα από εδώ
blog comments powered by Disqus