Μοριοδότηση 2018 - Εσπερινά
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(γ\)
Α2 - \(δ\)
Α3 - \(α\)
Α4 - \(δ\)
Α5: \(Λ - Σ - Λ - Σ - Λ\)
Θέμα Β
B1-\((i)\)
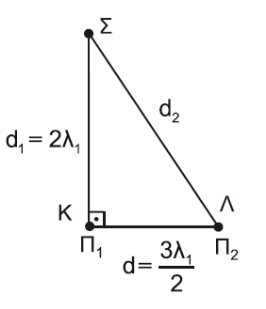
Ίδιο υλικό
\[υ_δ = λ_1 \cdot f_1 = λ_2 \cdot f_2 \overset{f_2=2\cdot f_1}{\implies} λ_2 = \frac{λ_1}{2}\] \[α) \underline {τρόπος}\] \[|A_Σ| = |2 A \cdot συν \frac{2π (d_1 - d_2)}{2 λ_2} | = |2 A \cdot συν \frac{π (2 λ_1 - \frac{5λ_1}{2} )}{\frac{λ_1}{2} }| = |2Α|\] \[β) \underline {τρόπος}\] \[\left. \begin{matrix}d_1 - d_2 = 2 λ_1 - \frac{5λ_1}{2} = - \frac{λ_1}{2} = -λ_2 \\\\ d_1 - d_2 = N \cdot λ_2\end{matrix} \right\} Ν = -1 \quad ενίσχυση\]Β2 - \((ιιι)\)
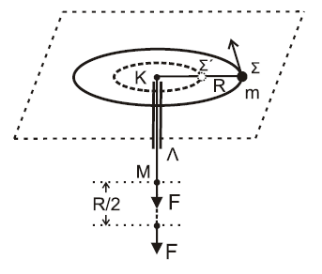
Η τάση του νήματος διέρχεται από τον άξονα περιστροφής
\[α) \underline {τρόπος}\] \[Άρα \quad m \cdot υ_1 \cdot R = m \cdot υ_2 \cdot \frac{R}{2} \Rightarrow υ_2 = 2 υ_1\] \[ΘΜΚΕ_m (Σ \rightarrow Σ') \quad Κ_{Σ'} - Κ_{Σ} = W_F \Rightarrow \frac{1}{2} \cdot m \cdot υ_2^2 - \frac{1}{2} \cdot m \cdot υ_1^2 = W_F\] \[\left. \begin{matrix} W_F = \frac{3}{2} \cdot m \cdot υ_1^2 \\\\ υ_1 = ω \cdot R\end{matrix} \right\} W_F = \frac{3}{2} \cdot m \cdot ω^2 \cdot R^2\] \[β) \underline {τρόπος}\] \[I_1 \cdot ω = Ι_2 \cdot ω´ \Rightarrow m \cdot R^2 \cdot ω = m \cdot \frac{R^2}{4} \cdot ω´ \Rightarrow ω´ = 4ω\] \[ΘΜΚΕ_m (Σ \rightarrow Σ') \quad Κ_{Σ'} - Κ_{Σ} = W_F \Rightarrow \frac{1}{2} \cdot Ι_2 \cdot ω´^2 - \frac{1}{2} \cdot Ι_1 \cdot ω^2 = W_F\] \[W_F = \frac{1}{2}m \frac{R^2}{4}16ω^2 - \frac{1}{2}m \cdot R^2 ω^2 \Rightarrow W_F = \frac{3}{2} \cdot m \cdot ω^2 \cdot R^2\]Β3 - \((ι)\)
Εξίσωση Bernoulli για μια ρευματική γραμμή \((Γ \rightarrow Δ)\)
\[P_Γ + \frac{1}{2}ρ \cdot υ_Γ^2 = P_Δ + \frac{1}{2}ρ \cdot υ_Δ^2 + ρ \cdot g \cdot h\]Εξίσωση συνέχειας \((Γ \rightarrow Δ)\)
\[Π_Γ = Π_Δ \Rightarrow Α_Γ \cdot υ_Γ = Α_Δ \cdot υ_Δ \overset{Α_Γ = 2Α_Δ}{\implies} υ_Δ = 2υ_Γ\]Οριζόντια βολή \((Δ \rightarrow Κ)\)
\[\left. \begin{matrix} h = \frac{1}{2} g \cdot t^2 \\\\ 4h = υ_Δ \cdot t\end{matrix} \right\} 4h = υ_Δ \cdot \sqrt{\frac{2h}{g}} \Rightarrow υ_Δ^2 = 8g\cdot h \overset{υ_Δ = 2υ_Γ}{\implies} 4υ_Γ^2 = 8g\cdot h \Rightarrow υ_Γ^2 = 2g \cdot h\] \[g\cdot h = \frac{υ_Γ^2}{2}\]Άρα η εξίσωση Bernoulli γράφεται
\[P_Γ - P_Δ = \frac{1}{2}ρ \cdot υ_Δ^2 + ρ \cdot g \cdot h - \frac{1}{2}ρ \cdot υ_Γ^2 = \frac{1}{2}ρ \cdot 4 υ_Γ^2 + ρ \cdot \frac{υ_Γ^2}{2} - \frac{1}{2}ρ \cdot υ_Γ^2 = 2 ρ \cdot υ_Γ^2\]Θέμα Γ
Γ1
\[K_1-m, \quad ΑΑΤ: D_1 = k_1 = m_1 \cdot ω_1^2 \Rightarrow ω_1 = \sqrt{\frac{k}{m}} = 5 \frac{rad}{sec}\] \[υ_{max1} = ω_1 \cdot A_1 = \sqrt{\frac{k}{m}} \cdot Δl = 2 \frac{m}{sec}\] \[ΑΔΟ \quad m_1, m_2 \quad (Θ.Ι.) \quad m_1 \cdot υ_{max1} = (m_1 + m_2) \cdot V \Rightarrow V = 1 \frac{m}{sec}\]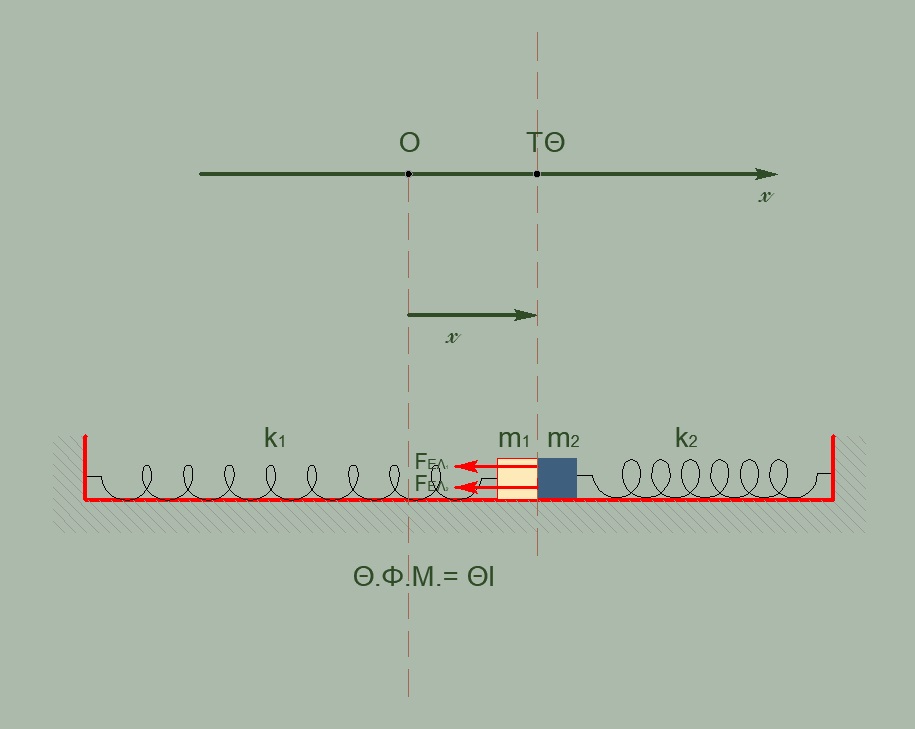
Στη θέση Θ.Φ.Μ. \(ΣF=0\) άρα αυτή είναι και Θ.Ι.
\[Τ.Θ.: ΣF = -F_{ΕΛ1} - F_{ΕΛ2} = -k_1 \cdot x - k_2 \cdot x = - (2k)x\]Για να εκτελεί ένα σώμα ΑΑΤ πρέπει να ισχύει
\[ΣF = -D \cdot x, D = 2k = (m_1 + m_2) ω^2 \Rightarrow ω = \sqrt{\frac{2k}{2m}} = \sqrt{\frac{k}{m}} = 5 \frac{rad}{sec}\] \[Θ.Ι.: V = υ_{max} \overset{υ_{max} = ω \cdot A}{\implies} 1 = 5 \cdot A \Rightarrow A = 0.2m\]Γ2
\[x = A \cdot ημ(ωt + φ_ο)\]όπου \(Α = 0.2 m\) και \(ω = \sqrt{\frac{2k}{2m}} = 5 \frac{rad}{s}\).
Για \(t=0, x=0, υ=V_{max} \Rightarrow φ_ο = 0\)
\[x = 0.2 ημ5t\]Γ3
\[|\frac{dp}{dt}|_{m_1+m_2(max)} = ΣF_{max} = D \cdot A \overset{D = 100 \frac{N}{m}}{\implies} ΣF_{max}=20N, \quad ή \quad \frac{kg \cdot m}{sec^2}\]Θέμα Δ
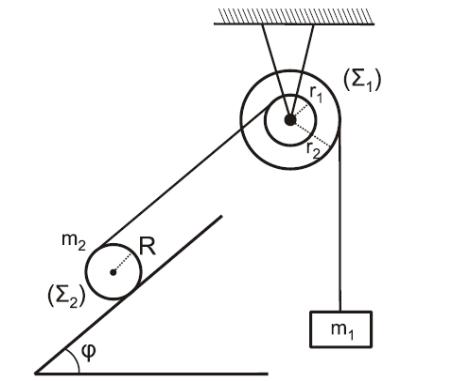
Τροχαλία (τροχ)
\[r_1 = 0.1 m\] \[r_2 = 0.2 m\] \[I_{cm(τροχ)} = 0.48 kg \cdot m^2\]Κύλινδρος
\[m_2 = 20 kg\]Σώμα μάζας \(m_1 = 3kg\)
\[ημφ = 0.6\] \[g = 10 \frac{m}{sec^2}\]Δ1
m MET:
\[ΣF_1 = 0 \Rightarrow T_1 = m_1 \cdot g \Rightarrow T_1 = 30N\]Τροχαλία
\[Στ = 0 \Rightarrow T_1 \cdot r_2 = T_2 \cdot r_1 \Rightarrow T_2 = 60N\]Δ2
Εφόσον το νήμα κόβεται, ο κύλινδρος εκτελεί κύλιση χωρίς ολίσθηση.
κύλινδρος ΜΕΤ:
\[m_2 \cdot g \cdot ημφ - Τ = m_2 \cdot α_{cm}\]κύλινδρος ΣΤΡΟΦ:
\[Στ = Ι \cdot α_{γων} \Rightarrow T \cdot R = \frac{1}{2} \cdot m_2 \cdot R^2 \cdot \frac{α_{cm}}{R} \Rightarrow T = \frac{1}{2} \cdot m_2 \cdot α_{cm}\]οπότε
\[m_2 \cdot g \cdot ημφ - \frac{1}{2} \cdot m_2 \cdot α_{cm} = m_2 \cdot α_{cm} \Rightarrow m_2 \cdot g \cdot ημφ = \frac{3}{2} \cdot m_2 \cdot α_{cm} \Rightarrow α_{cm} = \frac{2}{3} \cdot g \cdot ημφ \Rightarrow α_{cm} = 4 \frac{m}{s^2}\]Δ3
m1 MET:
\[ΣF_1 = m_1 \cdot α_1 \Rightarrow m_1 \cdot g - T_1 = m_1 \cdot α_1\]τροχαλία ΣΤΡΟΦ:
\[Στ = I \cdot α_{γων} \Rightarrow Τ_1 \cdot r_2 = I \cdot \frac{α_1}{r_2} \Rightarrow T_1 = I \cdot \frac{α_1}{r_2^2}\]και κάνοντας τις πράξεις \(α_1 = 2 \frac{m}{sec^2}\)
Δ4
m_1,
\[h = \frac{1}{2} \cdot α_1 \cdot t^2 \Rightarrow t = 0.5sec\] \[υ_1 = α \cdot t_1 \Rightarrow υ_1 = 1 \frac{m}{sec}\] \[ΑΔΜΕ_{τροχ-Δ} (Ι \rightarrow II): K_I + U_1 = K_{II} + U_{II}\] \[Ε_{μηχ(αρχ)} = Ε_{μηχ(τελ)}\] \[U_{αρχ} + Κ_{αρχ} = U_{τελ} + Κ_{τελ} \Rightarrow m_1 \cdot g \cdot h = K_{στροφ} + \frac{1}{2} \cdot m \cdot υ_1^2 \Rightarrow K_{στροφ} = 6J\]blog comments powered by Disqus