Σύμφωνες πηγές
Στην επιφάνεια ενός υγρού βρίσκονται δύο σύμφωνες πηγές \(Π_1\) και \(Π_2\) που παράγουν εγκάρσια αρμονικά κύματα τα οποία διαδίδονται με ταχύτητα \(4 \frac{m}{s}\). Οι πηγές ξεκινούν να ταλαντώνονται με φορά προς τα πάνω (θετική φορά). Την χρονική στιγμή \(t=0\) ξεκινάει να ταλαντώνεται η πρώτη πηγή με εξίσωση
\[y_{Π_1} = 0,2 \cdot ημ10πt\]Την ίδια χρονική στιγμή η πηγή \(Π_2\) έχει ήδη εκτελέσει μισή ταλάντωση και η εξίσωση που περιγράφει την κίνησή της είναι η
\[y_{Π_2} = 0,2 \cdot ημ(10πt+π)\]1) Να βρείτε ποια χρονική στιγμή αρχίζει η συμβολή των κυμάτων σε ένα σημείο Σ της επιφάνειας που απέχει από την πηγή \(Π_1\) απόσταση \(r_1=2m\) και από την πηγή \(Π_2\) απόσταση \(r_2=3,2m\).
2) Να γράψετε την χρονική εξίσωση της απομάκρυνσης του υλικού σημείου Σ από την χρονική στιγμή \(t=0\) έως την χρονική στιγμή \(t=1s\).
3) Να κάνετε την γραφική παράσταση της προηγούμενης συνάρτησης.
Απάντηση:
1) Από τα δεδομένα της άσκησης έχουμε:
\[ω = \frac{2π}{Τ} \Rightarrow T = \frac{2π}{ω} \Rightarrow T = 0,2 s\] \[υ = \frac{λ}{Τ} \Rightarrow λ = υ \cdot T \Rightarrow λ = 0,8m\]Το κύμα από την πηγή \(Π_1\) φθάνει στο σημείο Σ την χρονική στιγμή
\[t_1 = \frac{r_1}{υ} \Rightarrow t_1 = 0,5 s\]ενώ από την πηγή \(Π_2\) φθάνει στο σημείο Σ σε χρονική διάρκεια
\[Δt = \frac{r_2}{υ} \Rightarrow t_2 = 0,8 s\]όμως η πηγή αυτή έχει ήδη ξεκινήσει την ταλάντωση \(\frac{T}{2} = 0,1 s\) νωρίτερα, άρα το κύμα φθάνει στο σημείο Σ την χρονική στιγμή \(t_2 = 0,7s\).
2) To κύμα που φθάνει από την πηγή \(Π_1\) έχει εξίσωση
\[y_1 = 0,2 \cdot ημ(10πt - 5π) = 0,2 \cdot ημ[10π(t-0,5)+0]\]εξίσωση που ισχύει για \(t \ge 0,5s\), ενώ το κύμα που φθάνει στο σημείο Σ από την πηγή \(Π_2\) έχει εξίσωση
\[y_2 = 0,2 \cdot ημ(10πt - 8π + π) = 0,2 \cdot ημ[10π(t-0,7)+0]\]εξίσωση που ισχύει για \(t \ge 0,7s\). Για την συμβολή των κυμάτων ισχύει η εξίσωση \(y = y_1 + y_2\) και μετά τις πράξεις
\[y = -0,4 \cdot ημ(10πt -6π) = 0,4 \cdot ημ(10πt - 5π) = 0,4 \cdot ημ[10π(t-0,7)+0)\]εξίσωση που ισχύει για \(t \ge 0,7s\). Άρα συνοπτικά για το σημείο Σ έχουμε την παρακάτω χρονική συνάρτηση
\[y_Σ = 0\]για χρόνο \(0\le t < 0,5s\)
\[y_Σ = 0,2 \cdot ημ[10π(t-0,5)+0]\]για χρόνο \(0,5s \le t < 0,7s\) και
\[y_Σ = 0,4 \cdot ημ[10π(t-0,7)+0]\]για χρόνο \(0,7s \le t < 1s\)
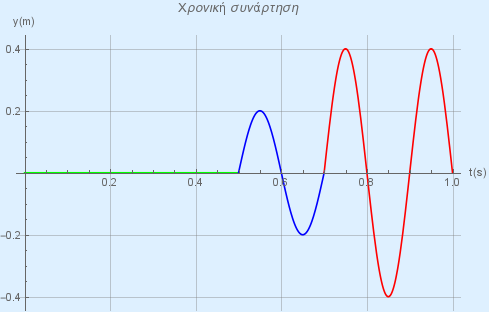
3) Τέλος η γραφική παράστασης της προηγούμενης συνάρτησης φαίνεται στο παρακάτω σχήμα.
και ο κώδικας σε mathematica
f[t] := 0
g[t] := 0.2Sin[10Pi(t-0.5)]
h[t] := 0.4Sin[10Pi(t-0.7)]
Show[{Plot[f[t], {t, 0, 0.5}, PlotStyle -> Green],
Plot[g[t], {t, 0.5, 0.7}, PlotStyle -> Blue],
Plot[h[t], {t, 0.7, 1}, PlotStyle -> Red]},
PlotRange -> All,
GridLines -> Automatic,
Background -> LightBlue,
PlotLabel -> "xroniki synartisi",
AxesLabel -> {"t(s)","y(m)"},
AxesOrigin -> {0, 0},
Filling -> Automatic]
blog comments powered by Disqus