Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2015
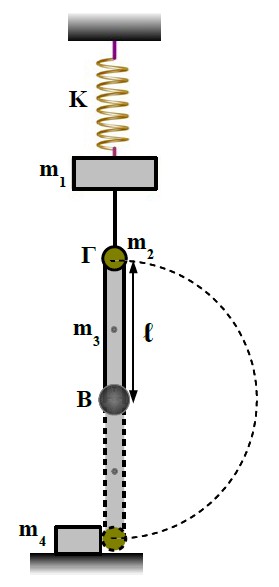
Κατακόρυφο ιδανικό ελατήριο σταθεράς \(Κ =100 \frac{Ν}{m}\) έχει ακλόνητα στερεωμένο το άνω άκρο του. Στο κάτω άκρο του ελατηρίου είναι τοποθετημένο σώμα μάζας \(m_1 =4 Kg\). Το σώμα μάζας \(m_1\) είναι δεμένο μέσω αβαρούς και μη εκτατού νήματος στο άνω άκρο \(Γ\) ομογενούς ράβδου \(ΒΓ\), μήκους \(l=2 m\) και μάζας \(m_3 =3 Kg\) που έχει ροπή αδράνειας \(I_{cm} = \frac{1}{12} \cdot m_3 \cdot l^2\). Στο άκρο \(Γ\) της ράβδου υπάρχει στερεωμένη μία σφαίρα μάζας \(m_2 =1 Kg\), αμελητέων διαστάσεων (βλέπε σχήμα). Αρχικά όλο το σύστημα ισορροπεί και η ράβδος είναι κατακόρυφη, ενώ η δύναμη στην άρθρωση στο άκρο \(Β\) της ράβδου είναι μηδέν.
Α. Να υπολογίσετε την αρχική παραμόρφωση του ελατηρίου από το φυσικό του μήκος στην κατάσταση ισορροπίας.
Β. Τη χρονική στιγμή \(t_0 =0\) δίνεται μία ελάχιστη ώθηση στη ράβδο (\(ω_0 \approx 0\)) και το νήμα σπάει. Το σώμα μάζας \(m_1\) εκτελεί απλή αρμονική ταλάντωση ενώ η ράβδος στρέφεται χωρίς τριβές γύρω από την άρθρωση στο άκρο \(Β\). Να γράψετε την εξίσωση της ταλάντωσης του σώματος μάζας \(m_1\), θεωρώντας θετική τη φορά προς τα πάνω.
Γ. Να υπολογίσετε τη γωνιακή ταχύτητα \(ω\) του συστήματος ράβδου-σφαίρας στην κατώτερη, κατακόρυφη θέση του.
Δ. Στην κατώτερη θέση του συστήματος ράβδου-σφαίρας, η σφαίρα συγκρούεται ελαστικά με σώμα μάζας \(m_4 =4 Kg\) το οποίο ισορροπεί πάνω σε λείο οριζόντιο επίπεδο. Να υπολογίσετε: τη γωνιακή ταχύτητα \(ω'\) του συστήματος ράβδου-σφαίρας και την ταχύτητα \(υ_4'\) του σώματος μάζας \(m_4\) , μετά την κρούση. Δίνεται: \(g=10 \frac{m}{s^2}\)
Απάντηση:
blog comments powered by Disqus