Μέγιστη Γωνιακή Επιτάχυνση
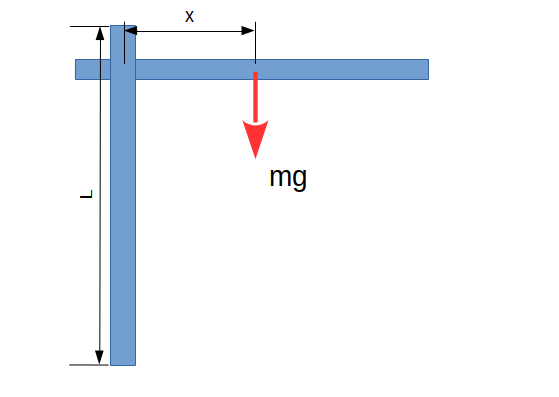
Ομογενής ράβδος μάζας \(m\) και μήκους \(L\), μπορεί να περιστρέφεται χωρίς τριβές σε κατακόρυφο επίπεδο γύρω από οριζόντιο άξονα που είναι κάθετος σε αυτή. Αφήνουμε ελεύθερη τη ράβδο να κινηθεί από την οριζόντια θέση. Αν η επιτάχυνση της βαρύτητας είναι \(g\), η ροπή αδράνειας της ράβδου ως προς άξονα περιστροφής που περνά από το κέντρο μάζας της δίνεται από την σχέση \(Ι = \frac{1}{12} \cdot m \cdot L^2\) και \(x\) είναι η απόσταση του κέντρου μάζας της ράβδου από τον οριζόντιο άξονα περιστροφής, όπως φαίνεται στο σχήμα, να βρείτε για ποια απόσταση \(x\) μεγιστοποιείται η αρχική γωνιακή επιτάχυνση \(α_{γων}\) της ράβδου.
Απάντηση:
Από το θεώρημα Steiner γνωρίζουμε ότι:
\[Ι_O = Ι_{cm} + m \cdot x^2 \Rightarrow I_O = \frac{1}{12} \cdot m \cdot L^2 + m \cdot x^2\]Οπότε από τον δεύτερο Νόμο του Νεύτωνα για τη στροφική κίνηση έχουμε:
\[Στ = Ι_Ο \cdot α_{γων} \Rightarrow α_{γων} = \frac{m \cdot g \cdot x}{\frac{1}{12} \cdot m \cdot L^2 + m \cdot x^2 }\]και απλοποιώντας τη μάζα έχουμε:
\[α_{γων} = \frac{g \cdot x}{\frac{L^2}{12}+x^2} \Rightarrow α_{γων} = \frac{g}{\frac{L^2}{12 \cdot x}+x}\]Για να γίνει αυτό το κλάσμα μέγιστο, θα πρέπει ο αριθμητής του να γίνει ελάχιστος.
α) τρόπος
Θεωρούμε την συνάρτηση \(f(x) = \frac{L^2}{12 \cdot x}+x\). Για να βρούμε σε ποια θέση \(x\) η συνάρτηση παρουσιάζει ακρότατο και συγκεκριμένα ελάχιστο, την παραγωγίζουμε και στη συνέχεια μηδενίζουμε την παράγωγο.
\[f'(x) = 0 \Rightarrow - \frac{L^2}{12 \cdot x^2} + 1 = 0 \Rightarrow \frac{L^2}{12 \cdot x^2} = 1 \Rightarrow x = \frac{L}{2 \cdot \sqrt3}\]β) τρόπος
Παρατηρούμε ότι ο παρανομαστής \(\frac{L^2}{12 \cdot x}+x\) αποτελείται από δύο όρους το γινόμενο των οποίων είναι σταθερός αριθμός, δηλαδή:
\[\frac{L^2}{12 \cdot x} \cdot x = \frac{L^2}{12}\]Θέλουμε να βρούμε πότε το άθροισμα αυτών των δύο όρων γίνεται ελάχιστο. Έστω για ευκολία \(α\) και \(β\) οι δύο όροι και \(λ\) το σταθερό τους γινόμενο. Δηλαδή \(α \cdot β = λ\). Γνωρίζουμε ότι
\[(α+β)^2 = (α-β)^2 + 4 \cdot α \cdot β = (α-β)^2 + 4\cdot λ \geqslant 4 \cdot λ\]Δηλαδή το άθροισμα των δύο όρων είναι
\[(α+β)^2 \geqslant 4 \cdot λ\]Οπότε η μικρότερη τιμή που μπορεί να πάρει είναι όταν \((α-β)^2 = 0 \Rightarrow α=β\)
\[(α+β)^2 = 4 \cdot λ \Rightarrow α+β = \sqrt{4 \cdot λ} = 2 \cdot \sqrtλ \Rightarrow α = β = \sqrtλ\]Έτσι για τα δεδομένα του προβλήματος
\[x = \sqrt{\frac{L^2}{12}} \Rightarrow x = \frac{L}{2 \cdot \sqrt3}\]blog comments powered by Disqus