Διακρότημα με παλμογράφο
Δύο αρμονικές Ταλαντώσεις ίδιας διεύθυνσης, που γίνονται γύρω από το ίδιο σημείο, με το ίδιο πλάτος και διαφορετικές συχνότητες περιγράφονται από τις ακόλουθες εξισώσεις:
\[x_1 = A \cdot ημ(ω_1 \cdot t + \frac{π}{2})\] \[x_2 = A \cdot ημ(ω_2 \cdot t + \frac{π}{2})\]Το αποτέλεσμα της σύνθεσης των δύο ταλαντώσεων παρουσιάζεται στην παρακάτω εικόνα
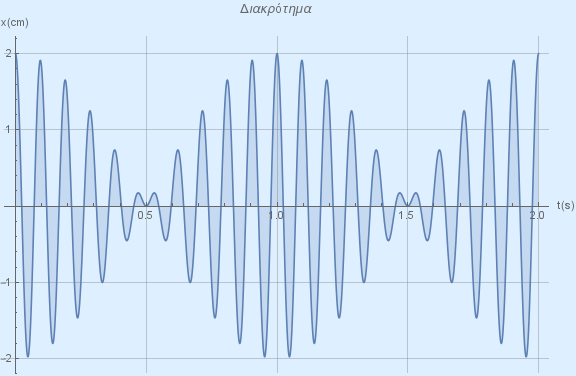
Εάν γνωρίζετε ότι \(ω_1 = 20 \cdot π \frac{rad}{s}\) να υπολογίσετε:
α) Τα πλάτη των δύο ταλαντώσεων
β) Την περίοδο του διακροτήματος
γ) Την εξίσωση που περιγράφει την ιδιόμορφη ταλάντωση που προκύπτει από την σύνθεση των δύο ταλαντώσεων
δ) Την κυκλική συχνότητα \(ω_2\) της δεύτερης ταλάντωσης.
Τις αρμονικές ταλαντώσεις μπορούμε να αναπαραστήσουμε με την βοήθεια δύο γεννητριών συχνοτήτων και ενός παλμογράφου όπως φαίνεται στο ακόλουθο βίντεο
Ο κώδικας σε mathematica
Plot[Sin[20*Pi*t+Pi/2]+Sin[22*Pi*t+Pi/2], {t, 0, 2},
PlotLegends ->"Expressions",
PlotRange -> All,
PlotLabel -> "Διακρότημα",
Background -> LightBlue,
GridLines -> Automatic,
AxesLabel -> {"t(s)", "x(cm)"},
Filling -> Automatic]
blog comments powered by Disqus