Διαγωνισμός Φυσικής Β. Ξανθόπουλος 2011
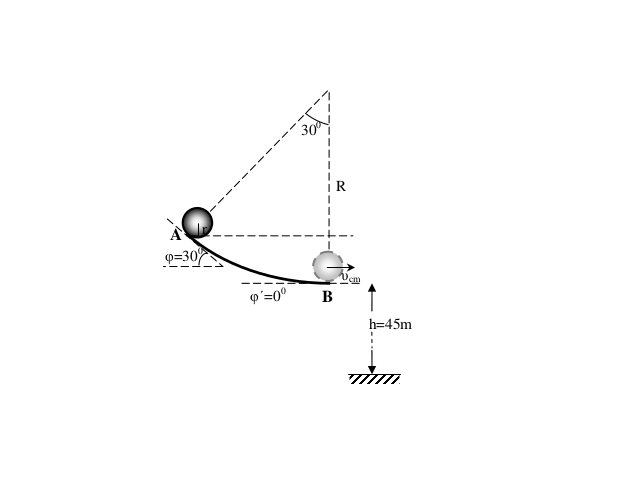
Ένας διάδρομος έχει σχήμα τόξου με επίκεντρη γωνία \(30^0\) και είναι τοποθετημένος έτσι ώστε το επίπεδο του να ταυτίζεται με το κατακόρυφο επίπεδο. Στο ένα άκρο \(Α\) ο διάδρομος σχηματίζει γωνία \(30^0\) με το οριζόντιο επίπεδο, ενώ στο άλλο σχηματίζει γωνία \(0^0\) (είναι οριζόντιος). Αφήνουμε από το άκρο \(Α\) του διαδρόμου ένα δίσκο, ο οποίος κυλά χωρίς να γλιστρά από το Α στο Β και κατόπιν πέφτει στο έδαφος.
α) Πόση είναι η αρχική επιτάχυνση που αποκτά το κέντρο μάζας του δίσκου στο σημείο \(Α\), τη στιγμή που αφήνεται ελεύθερος;
β) Πόσος είναι ο συντελεστής οριακής τριβής \(μ_S\) των επιφανειών δαπέδου – δίσκου, αν ξέρουμε ότι στο Α η στατική τριβή που δέχεται ο δίσκος έχει την οριακή της τιμή.
γ) Αν το λόγος της ακτίνας του δίσκου προς την ακτίνα του διαδρόμου είναι: \(\frac{r}{R} = \frac{1}{120}\), πόσες περιστροφές θα εκτελέσει ο δίσκος κατά την κίνηση του από το Α στο Β;
δ) Να αποδείξετε ότι κατά τη διάρκεια της πτώσης του από το άκρο Β μέχρι το έδαφος, το εκάστοτε κατώτερο σημείο του δίσκου έχει πάντα κατακόρυφη ταχύτητα και να υπολογίσετε το μέτρο της τη στιγμή που κτυπά στο έδαφος, αν το σημείο Β βρίσκεται σε ύψος \(h = 45m\).
Θεωρείστε: α) \(g = 10 \frac{m}{s^2}\), β) Η ροπή αδράνειας του δίσκου ως προς άξονα που περνά από το κέντρο του και είναι κάθετος σ’ αυτόν δίνεται από τη σχέση: \(Ι_{cm} = \frac{1}{2} \cdot m \cdot r^2\), γ) \(ημ30^0 = \frac{1}{2}\) και δ) ότι η αντίσταση του αέρα θεωρείται αμελητέα καθ’ όλη τη διάρκεια της κίνησης του δίσκου.
Απάντηση:
Μια ομιλία του Βασίλη Ξανθόπουλου στο ΑΠΘ εδώ
blog comments powered by Disqus