Ενδεικτικές Λύσεις B' Λυκείου
Ενδεικτικές απαντήσεις
Θέμα Α
Α1 - \(β\)
Α2 - \(γ\)
Α3 - \(γ\)
Α4 - \(γ\)
Α5 \(\quad Σ - Σ - Σ - Λ - Σ\)
Θέμα Β
A1
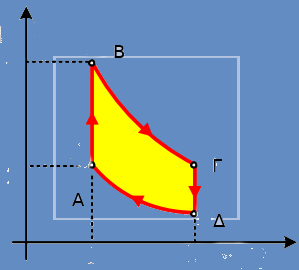
ΑΒ Ισόχωρη θέρμανση \(V = σταθ \Rightarrow \frac{P}{T} = σταθ \Rightarrow P = σταθ \cdot T\)
ΒΓ Ισόθερμη εκτόνωση \(T = σταθ \Rightarrow P \cdot V = σταθ \Rightarrow P = \frac{σταθ}{V}\)
ΓΔ Ισόχωρη ψύξη \(V = σταθ \Rightarrow \frac{P}{T} = σταθ \Rightarrow P = σταθ \cdot T\)
ΔΑ Ισόθερμη συμπίεση \(T = σταθ \Rightarrow P \cdot V = σταθ \Rightarrow P = \frac{σταθ}{V}\)
A2
B1 - \(υ_Δ = \sqrt{g_o \cdot R_Γ}\)
\[\underline {α) τρόπος}\] \[ΑΔΜΕ_{1 -> \infty} \Rightarrow K_1 + U_1 = K_{\infty} + U_{\infty} \Rightarrow \frac{1}{2} \cdot m \cdot υ^2 - G \cdot \frac{M \cdot m}{R_Γ + h} = 0 + 0\]και γνωρίζουμε ότι \(g_o = \frac{G \cdot M}{R^2}\)
\[\frac{1}{2} \cdot m \cdot υ_Δ^2 - G \cdot \frac{M \cdot m}{2 \cdot R_Γ} = 0 \Rightarrow υ_Δ^2 = \frac{G \cdot M}{R_Γ} \Rightarrow υ_Δ^2 = g_o \cdot R_Γ \Rightarrow υ_Δ = \sqrt{g_o \cdot R_Γ}\] \[\underline {β) τρόπος}\] \[ΔΚ = ΣW \Rightarrow K_{ΤΕΛ} - Κ_{ΑΡΧ} = -W_F \Rightarrow 0 - \frac{1}{2} \cdot m \cdot υ_Δ^2 = ΔU \Rightarrow - \frac{1}{2} \cdot m \cdot υ_Δ^2 = (0 - U_{αρχ}) \Rightarrow - \frac{1}{2} \cdot m \cdot υ_Δ^2 = - G \cdot \frac{M \cdot m}{2 \cdot R_Γ}\] \[υ_Δ^2 = \frac{G \cdot M}{R_Γ} \Rightarrow υ_Δ^2 = g_o \cdot R_Γ \Rightarrow υ_Δ = \sqrt{g_o \cdot R_Γ}\] \[\underline {γ) τρόπος}\]Με μαθηματικά Γ´ Λυκείου
\[ΔΚ = ΣW \Rightarrow K_{ΤΕΛ} - Κ_{ΑΡΧ} = W_F \Rightarrow 0 - \frac{1}{2} \cdot m \cdot υ_Δ^2 = \int_{r=R_Γ+h}^{r= \infty} Fdr \Rightarrow - \frac{1}{2} \cdot m \cdot υ_Δ^2 = \int_{r=2R_Γ}^{r= \infty} \frac{G \cdot M \cdot m}{r^2}dr \Rightarrow - \frac{1}{2} \cdot m \cdot υ_Δ^2 = -\frac{G \cdot M \cdot m}{r} \Big|_{r=2R_Γ}^{r= \infty}\] \[\frac{1}{2} \cdot m \cdot υ_Δ^2 = G \cdot \frac{M \cdot m}{2 \cdot R_Γ} \Rightarrowυ_Δ^2 = \frac{G \cdot M}{R_Γ} \Rightarrow υ_Δ^2 = g_o \cdot R_Γ \Rightarrow υ_Δ = \sqrt{g_o \cdot R_Γ}\]Θέμα Γ
Γ1
\[ΣF_{εξ} = 0 \Rightarrow p_{πριν} = p_{μετά} \Rightarrow m_2 \cdot υ_ο = (m_1 + m_2) \cdot V \Rightarrow V = 5 \frac{m}{s}\]Γ2
\[Q = K_{πριν} - Κ_{μετά} \Rightarrow Q = \frac{1}{2} \cdot m_2 \cdot υ_ο^2 - \frac{1}{2} \cdot (m_1 + m_2) \cdot V^2 \Rightarrow Q = 150 Joule\]Γ3
\[υ = ω \cdot R \Rightarrow V = ω \cdot L \Rightarrow ω = 10 \frac{rad}{s}\]Γ4
\[F_κ = \frac{m \cdot υ^2}{R} \Rightarrow F_κ = \frac{(m_1 + m_2) \cdot V^2}{L} \Rightarrow F_κ = 200 Ν\]Θέμα Δ
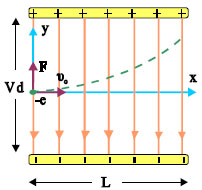
Οριζόντια βολή (κίνηση σε ομογενές ηλεκτρικό πεδίο)
Άξονας x
\[ΣF_x = 0\] \[α_x = 0\] \[υ_x = υ_ο\] \[x = υ_ο \cdot t\]Άξονας y
\[ΣF_y = E \cdot q = \frac{V}{d} \cdot q\] \[α_y = \frac{V \cdot q}{d \cdot m}\] \[υ_y = 0\] \[y = \frac{1}{2} \cdot α \cdot t^2\]Δ1
\[C = \frac{Q}{V} \Rightarrow V = \frac{Q}{C} \Rightarrow V = 40 Volt\]Δ2
\[t = \frac{L}{υ_ο} \Rightarrow t = 2.4 \cdot 10^{-4} sec\]Δ3
\[y = \frac{1}{2} \cdot \frac{V \cdot q}{d \cdot m} \cdot t^2 \Rightarrow y = 14.4 \cdot 10^{-4} m\]Δ4
\[\underline {α) τρόπος}\] \[V_x = \frac{W_x}{q} = \frac{F \cdot y}{q} = \frac{E \cdot q \cdot y}{q} = \frac{V \cdot y}{d} = 28.8 Volt\] \[\underline {β) τρόπος}\] \[V = E \cdot d\] \[V_x = E \cdot y\] \[V_x = \frac{V \cdot y}{d} \Rightarrow V_x = 28.8 Volt\] \[\underline {γ) τρόπος}\](Χωρίς τύπους) Το ηλεκτρικό πεδίο είναι ομογενές. Αυτό σημαίνει ότι η ένταση του ηλεκτρικού πεδίου είναι σταθερή. Την ένταση \(Ε\) την μετράμε σε \(\frac{N}{C}\) ή σε \(\frac{Volt}{m}\). Στο ομογενές ηλεκτρικό πεδίο της άσκησης υπολογίσαμε στο πρώτο ερώτημα ότι για κάθε δύο χιλιοστά, πάνω σε μια δυναμική γραμμή η διαφορά δυναμικού είναι \(40 Volt\). Οπότε για κάθε χιλιοστό απόστασης η διαφορά δυναμικού είναι \(20 Volt\). Αφού η απόκλιση είναι \(1,44\) χιλιοστά κατά μήκος μιας δυναμικής γραμμής, η διαφορά δυναμικού που ζητείται είναι \(1.44 \cdot 20 = 28.8 Volt\).
blog comments powered by Disqus