Η "Ένταση" στην Φυσική Μια συζήτηση για το μέγεθος της έντασης
Ας ξεκινήσουμε με τα λιγότερο γνωστά . Η ένταση ορίζεται ως ενέργεια ανά χρόνο και ανά επιφάνεια. Δηλαδή είναι ισχύς ανά επιφάνεια. Αφού η ισχύς ορίζεται ως ενέργεια ανά χρόνο.
\(1. \quad Ένταση \quad φωτεινής \quad πηγής.\) Συμβολίζεται με το γράμμα \(Ι\) αρχικό της λέξης intensity, Luminous Intensity (Φωτεινή ένταση). Μονάδα μέτρηση του μεγέθους ένταση φωτεινής πηγής είναι η candela (cd) και ορίζεται ως εξής:
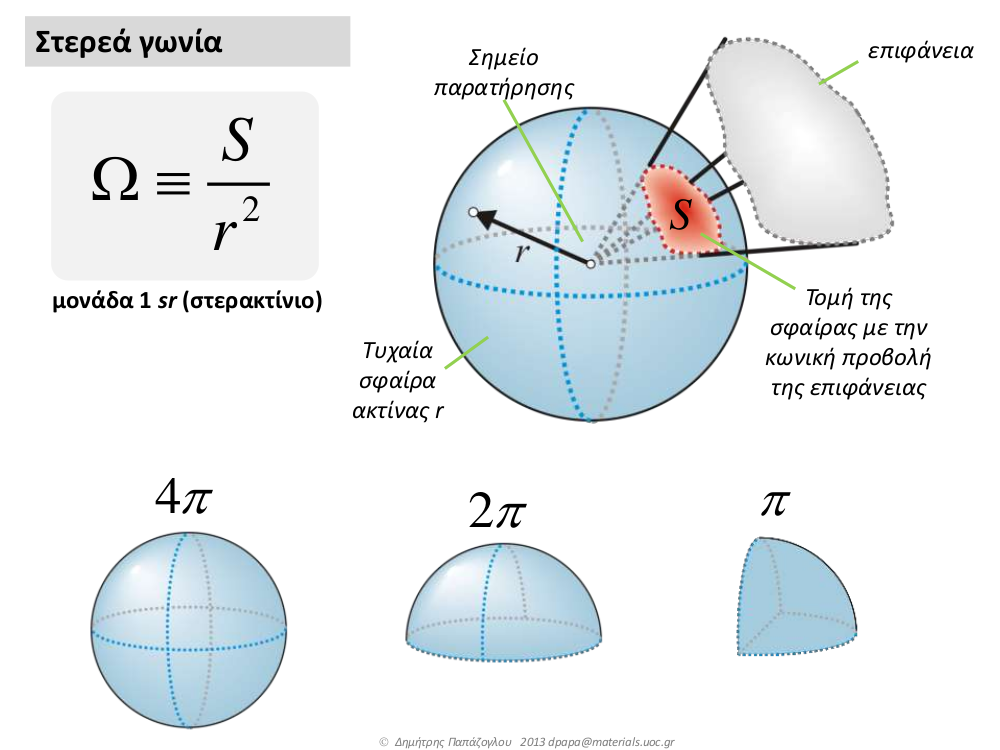
\[Ι = \frac{dΦ}{dΩ}\]όπου \(Φ\) είναι η φωτεινή ροή (Luminous flux) και μετριέται σε lumen (lm) ενώ \(Ω\) είναι η στερεά γωνία και μετριέται σε στερακτίνια (sr).
\(2. \quad Ένταση \quad ηχητικής \quad πηγής.\) Συμβολίζεται με το γράμμα \(Ι\) αρχικό της λέξης intensity, Acoustic Source Intensity. Μονάδα μέτρησης του μεγέθους ένταση ηχητικής πηγής είναι στο S.I. το \(\frac{W}{m^2}\). Η ελάχιστη ένταση που γίνεται αντιληπτή στο ανθρώπινο αυτί αντιστοιχεί σε \(10^{-12} \frac{W}{m^2}\). Η ένταση αυτή αντιστοιχεί σε ηχητική πίεση \(20 μPa\), η οποία αναφέρεται στην βιβλιογραφία και ως κατώφλι ακουστότητας. Η στάθμη της έντασης του ήχου μετράται σε Ντεσιμπέλ (decibel). Η μονάδα Ντεσιμπέλ εκφράζει την διαφορά στάθμης ενός ήχου έντασης \(Ι\) προς την ένταση του κατωφλίου ακουστότητας (\(10^{-12} \frac{W}{m^2}\)). Ως στάθμη έντασης σε \(dB\) ορίζεται το δεκαπλάσιο του δεκαδικού λογάριθμου της έντασης του ήχου προς την ένταση του κατωφλίου ακουστότητας, και περιγράφεται μαθηματικά από την σχέση:
\[L_I = 10 \cdot log_{10} (\frac{I_1}{I_0}) \quad dB\]Η ένταση ηχητικής πηγής ορίζεται ως εξής:
\[Ι = \frac{W}{A} \Rightarrow I = \frac{W}{4πr^2}\]όπου \(W\) η ισχύς της ηχητικής πηγής και \(r\) η απόσταση από την πηγή.
\(3. \quad Ένταση \quad ηλεκρικού \quad ρεύματος.\) Συμβολίζεται με το γράμμα \(Ι\) αρχικό της λέξης intensité du courant που χρησιμοποίησε πρώτος ο André-Marie Ampère. Μονάδα μέτρησης του μεγέθους ένταση ηλεκτρικού ρεύματος είναι το Α (Ampere) και είναι θεμελιώδης μονάδα μέτρησης για το S.I. H ένταση του ηλεκτρικού ρεύματος εκφράζει τον ρυθμό διέλευσης του ηλεκτρικού φορτίου από τη διατομή ενός αγωγού. Πιο απλά, η ένταση του ηλεκτρικού ρεύματος μας δείχνει πόσο ηλεκτρικό φορτίο περνάει από τη διατομή ενός αγωγού σε συγκεκριμένο χρονικό διάστημα. Ορίζεται ως εξής:
\[Ι = \frac{dQ}{dt}\]Οι επόμενες τρεις εντάσεις είναι εντάσεις πεδίων και για αυτόν τον λόγο είναι διανυσματικά μεγέθη. Η ένταση ενός πεδίου ορίζεται ως το πηλίκο της δύναμης του πεδίου προς την αιτία που δημιούργησε το πεδίο.
\(4. \quad Ένταση \quad βαρυτικού \quad πεδίου.\) Συμβολίζεται με το γράμμα \(g\) αρχικό της λέξης gravity. Μονάδα μέτρησης της έντασης του βαρυτικού πεδίου είναι το \(\frac{m}{s^2}\). Η ένταση του βαρυτικού πεδίου είναι το φυσικό διανυσματικό μέγεθος που έχει μέτρο ίσο με το πηλίκο της δύναμης που ασκείται σε ένα σώμα μάζας \(m\) που βρίσκεται σε απόσταση \(r\) από το κέντρο της πηγής βαρύτητας προς τη μάζα \(m\) του σώματος στο οποίο ασκείται η δύναμη του βαρυτικού πεδίου. Ορίζεται ως εξής:
\[\vec{g} = \frac{\vec{B}}{m}\]Όπου \(Β\) είναι η δύναμη που δέχεται μια σημειακή μάζα \(m\) όταν τοποθετείται σε ένα σημείο \(Α\) που απέχει απόσταση \(r\) από την σημειακή μάζα \(Μ\) που είναι η αιτία δημιουργίας του βαρυτικού πεδίου.
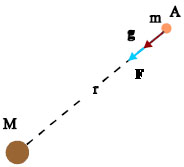
Ο νόμος του Νεύτωνα για τη βαρύτητα διατυπώνεται ως εξής: «Κάθε σώμα στο σύμπαν έλκει κάθε άλλο σώμα με δύναμη ανάλογη του γινομένου των μαζών τους και αντιστρόφως ανάλογη του τετραγώνου της απόστασης του κέντρου μάζας τους». Ο νόμος αυτός εκφράζεται ως εξής:
\[Β = G \frac{M \cdot m}{r^2}\]Οπότε συνδυάζοντας τις δύο τελευταίες σχέσεις έχουμε για την ένταση του βαρυτικού πεδίου (που συχνά αναφέρεται και ως επιτάχυνση της βαρύτητας) την σχέση:
\[g = \frac{G \cdot M}{r^2}\]\(5. \quad Ένταση \quad ηλεκτρικού \quad πεδίου.\) Συμβολίζεται με το γράμμα \(Ε\) αρχικό της λέξης Electric Field. Μονάδα μέτρησης της έντασης του ηλεκτρικού πεδίου είναι το \(\frac{Ν}{C}\). Ένταση του ηλεκτρικού πεδίου ονομάζουμε το φυσικό διανυσματικό μέγεθος που έχει μέτρο ίσο με το πηλίκο του μέτρου της δύναμης που ασκείται σε φορτίο \(q\) που βρίσκεται σε αυτό το σημείο προς το φορτίο αυτό και κατεύθυνση την κατεύθυνση της δύναμης, αν αυτή ασκείται σε θετικό φορτίο. Συνηθίζεται να χρησιμοποιούμε τον όρο «ηλεκτρικό πεδίο» αντί του ορθού «ηλεκτροστατικό πεδίο». Ηλεκτροστατικό πεδίο Coulomb ονομάζουμε το πεδίο που δημιουργείται από ένα ακίνητο σημειακό φορτίο \(Q\). H ένταση του ηλεκτρικού πεδίου ορίζεται ως εξής:
\[\vec{Ε} = \frac{\vec{F}}{q}\]Όπου \(F\) είναι η δύναμη Coulomb που δέχεται ένα δοκιμαστικό φορτίο \(q\) όταν τοποθετείται σε ένα σημείο \(Α\) που απέχει απόσταση \(r\) από ακίνητο σημειακό ηλεκτρικό φορτίο \(Q\) το οποίο ονομάζουμε πηγή του πεδίου.
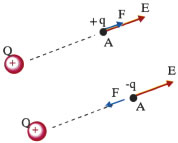
Ο Charles Augustin Coulomb το 1784 μετά από μία σειρά πειραμάτων, κατάφερε να μετρήσει τις δυνάμεις που αναπτύσσονται μεταξύ ηλεκτρικών φορτίων. Τα συμπεράσματα διατύπωσε με τον παρακάτω νόμο που φέρει το όνομά του. «Κάθε σημειακό ηλεκτρικό φορτίο ασκεί δύναμη σε κάθε άλλο σημειακό ηλεκτρικό φορτίο. Το μέτρο της δύναμης είναι ανάλογο του γινομένου των φορτίων που αλληλεπιδρούν και αντίστροφα ανάλογο με το τετράγωνο της μεταξύ τους απόστασης. Το μέτρο αυτής της δύναμης δίνεται από την σχέση:
\[F = k \frac{|Q \cdot q|}{r^2}\]Οπότε συνδυάζοντας τις δύο τελευταίες σχέσεις έχουμε για την ένταση του ηλεκτρικού πεδίου την σχέση:
\[Ε = k \frac{|Q|}{r^2}\]\(6. \quad Ένταση \quad Μαγνητικού \quad Πεδίου.\) Συμβολίζεται με το γράμμα \(Β\). Υπάρχουν διάφορες εξηγήσεις για την προέλευση του συμβόλου.
Κάποιοι αναφέρονται στον Γάλλο Φυσικό Αστρονόμο και Μαθηματικό Jean-Baptiste Biot που μαζί με τον Felix Savart διατύπωσαν τον νόμο Biot και Savart μιας και βρήκαν πειραματικά ότι ένα στοιχειώδες τμήμα \(dl\) ενός αγωγού που διαρρέεται από ρεύμα έντασης \(Ι\), δημιουργεί σε απόσταση \(r\) μία στοιχειώδη μαγνητική επαγωγή \(dB\), η οποία δίνεται από την σχέση:
\[dB = \frac{μ_ο}{4π} \cdot \frac{I \cdot dl \cdot ημθ}{r^2}\]Άλλοι αναφέρουν ότι ότι το γράμμα \(Β\) επιλέχθηκε λόγω των γραμμών πεδίου και το σύμβολο αναφέρεται στον όρο “Βορράς” που είναι μετάφραση του όρου Boreal.
Τέλος υπάρχει και η αναφορά ότι το σύμβολο οφείλεται στον James Clerk Maxwell o οποίος χρησιμοποίησε κατά σειρά τα γράμματα A, B, C, D, E, F, G, H, I, J όπως παρακάτω:
A A vector potential
B B magnetic field B
C I total current (through a cross section)
D D electric displacement field
E E electric field
F f force density (f = ρE + JxB)
G v velocity in a point
H H magnetic field H
I M magnetization M
J J current density
Η μονάδα μέτρησης της έντασης του μαγνητικού πεδίου ονομάζεται Tesla προς τιμή του Κροάτη φυσικού και εφευρέτη Nicola Tesla και συμβολίζεται με \(Τ\). Ο ορισμός του μέτρου της έντασης του μαγνητικού πεδίου προκύπτει από τον τύπο του νόμου του Laplace. Το μέτρο της έντασης μαγνητικού πεδίου είναι ίσο με το πηλίκο της δύναμης Laplace που ασκείται σε ευθύγραμμο ρευματοφόρο αγωγό προς το γινόμενο της έντασης \(I\) του ρεύματος επί το μήκος \(ℓ\) του αγωγού που βρίσκεται μέσα σε μαγνητικό πεδίο, όταν αυτός τοποθετηθεί κάθετα στις δυναμικές γραμμές, δηλαδή:
\[\vecΒ = \frac{\vec{F_L}}{I \cdot l}\]Ανακεφαλαιώνοντας η αιτία δημιουργίας του βαρυτικού πεδίου είναι η βαρυτική μάζα, η αιτία δημιουργίας του ηλεκτρικού πεδίου είναι το ακίνητο ηλεκτρικό φορτίο, ενώ η αιτία δημιουργίας του μαγνητικού πεδίου είναι το κινούμενο ηλεκτρικό φορτίο.
blog comments powered by Disqus