Ενδεικτικές Λύσεις A' Λυκείου
Ενδεικτικές απαντήσεις
Θέμα Α
Α1 - \(α\)
Α2 - \(β\)
Α3 - \(β\)
Α4 \(\quad 1Γ, 2Δ, 3Ε, 4Α, 5Β, 6ΣΤ\)
Α5 \(\quad Λ - Σ - Σ - Λ - Λ\)
Θέμα Β
B1 \(\quad x = x_o + υ \cdot (t - t_o)\)
Απόδειξη:
\[υ = \frac{Δx}{Δt} \Rightarrow υ = \frac{x - x_ο}{t - t_o} \Rightarrow x - x_ο = υ \cdot (t - t_o) \Rightarrow x = x_o + υ \cdot (t - t_o)\]B2 \(\quad υ = υ_o + α \cdot (t - t_o)\)
Απόδειξη:
\[α = \frac{Δυ}{Δt} \Rightarrow α = \frac{υ - υ_ο}{t - t_o} \Rightarrow υ - υ_ο = α \cdot (t - t_o) \Rightarrow υ = υ_o + α \cdot (t - t_o)\]Β3
Μαθηματική διατύπωση: \(\overrightarrow{F_{AB}} = - \overrightarrow{F_{BA}}\)
Θεωρητική διατύπωση.
Όταν δύο σώματα αλληλεπιδρούν και το πρώτο ασκεί δύναμη \(\overrightarrow{F}\) στο δεύτερο, τότε και το δεύτερο ασκεί αντίθετη δύναμη \(-\overrightarrow{F}\) στο πρώτο.
Θέμα Γ
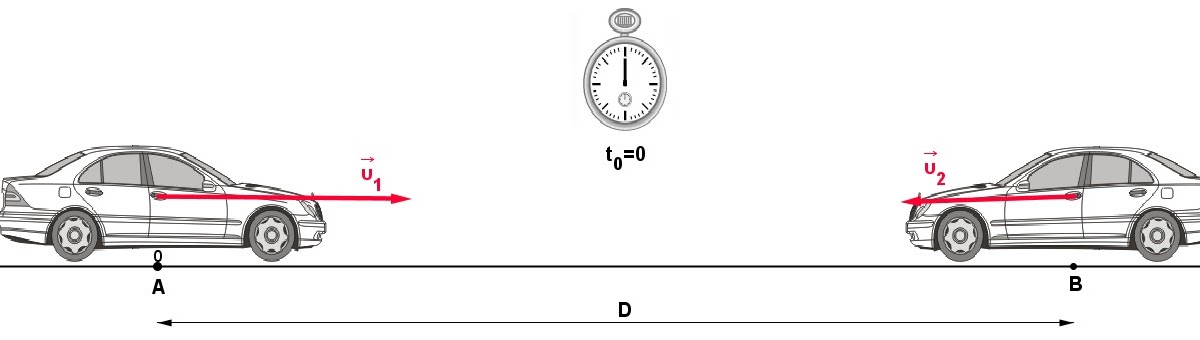
Γ1
Δεδομένα
\[D = 500m\] \[υ_1 = 30\frac{m}{sec}\] \[υ_2 = 20\frac{m}{sec}\] \[t_o = 0sec\]α. Η μετατόπιση κάθε αυτοκινήτου βρίσκεται ως εξής:
\[Δx_1 = υ_1 \cdot Δt \Rightarrow Δx_1 = υ_1 \cdot (t_1 - t_o) \Rightarrow Δx_1 = 30 \cdot (5 - 0) \Rightarrow Δx_1 = 150m\] \[Δx_2 = υ_2 \cdot Δt \Rightarrow Δx_2 = υ_2 \cdot (t_1 - t_o) \Rightarrow Δx_1 = 20 \cdot (5 - 0) \Rightarrow Δx_2 = 100m\]β. Η θέση κάθε αυτοκινήτου βρίσκεται από την εξίσωση κίνησης \(x = x_o + υ \cdot (t - t_o)\)
\[x_1 = x_o + υ_1 \cdot (t_1 - t_o) = 0 + 30 \cdot (5 - 0) = 150m\] \[x_2 = x_o + υ_2 \cdot (t_1 - t_o) = 500 - 20 \cdot (5 - 0) = 400m\]γ. H απόσταση \(D'\) μεταξύ των αυτοκινήτων είναι
\[D' = x_2 - x_1 = 400 - 150 = 250m\]Γ2
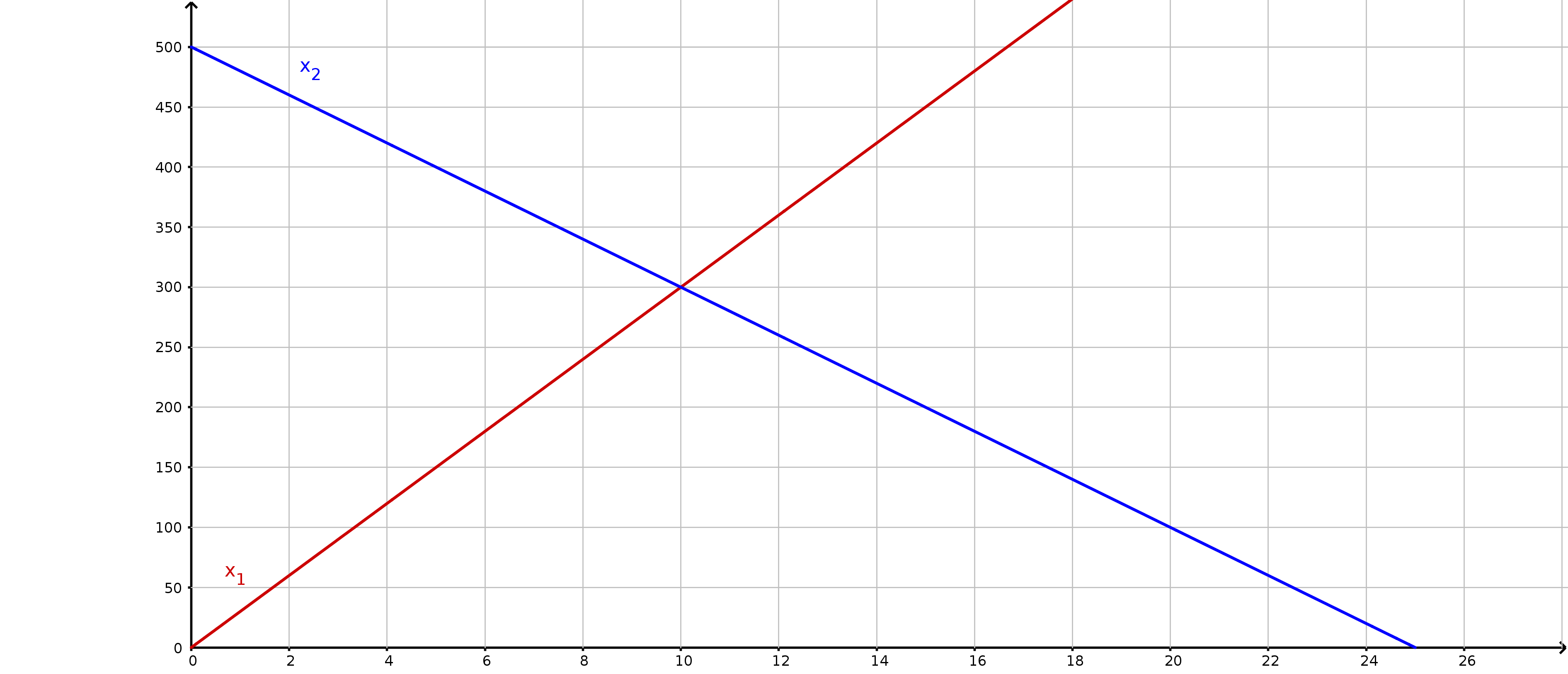
\[\underline {α) τρόπος}\] \[Δx_1 = υ_1 \cdot t_s \Rightarrow Δx_1 = 30 \cdot t_s\] \[Δx_2 = υ_2 \cdot t_s \Rightarrow Δx_2 = 20 \cdot t_s\] \[Δx_1 + Δx_2 = D \Rightarrow 30 \cdot t_s + 20 \cdot t_s = 500 \Rightarrow t_s = 10sec\] \[\underline {β) τρόπος}\] \[x = x_o + υ \cdot (t - t_o)\] \[x_1 = x_o + υ_1 \cdot (t_s - t_o) \Rightarrow x_1 = 0 + 30 \cdot (t_s - 0) \Rightarrow x_1 = 30 \cdot t_s\] \[x_2 = x_o + υ_2 \cdot (t_s - t_o) \Rightarrow x_1 = 500 - 20 \cdot (t_s - 0) \Rightarrow x_2 = 500 - 20 \cdot t_s\] \[x_1 = x_2 \Rightarrow 30 \cdot t_s = 500 - 20 \cdot t_s \Rightarrow t_s = 10sec\] \[\underline {γ) τρόπος}\]Κάνουμε τις γραφικές παραστάσεις των εξισώσεων κίνησης των δύο κινητών
\[x_1 = 30 \cdot t_s\] \[x_2 = 500 - 20 \cdot t_s\]και από το σχήμα βλέπουμε σε ποια χρονική στιγμή τα κινητά βρίσκονται στην ίδια θέση
(χωρίς τύπους) Η απόσταση που χωρίζει τα αυτοκίνητα είναι 500 μέτρα. Κάθε δευτερόλεπτο το κάθε αυτοκίνητο καλύπτει 30 και 20 μέτρα αντίστοιχα αυτής της απόστασης, δηλαδή συνολικά κάθε δευτερόλεπτο καλύπτονται 50 μέτρα απόστασης. Με απλή μέθοδο των τριών καταλαβαίνουμε ότι σε 10 δευτερόλεπτα θα καλυφθεί η απόσταση και άρα θα συναντηθούν τα αυτοκίνητα.
Τα αυτοκίνητα θα συναντηθούν στην θέση
\[x_1 = x_o + υ_1 \cdot (t_s - t_o) = 0 + 30 \cdot (10 - 0) = 300m\]Γ3
Τα διαγράμματα ταχύτητας χρόνου
Τα διαγράμματα μετατόπισης χρόνου
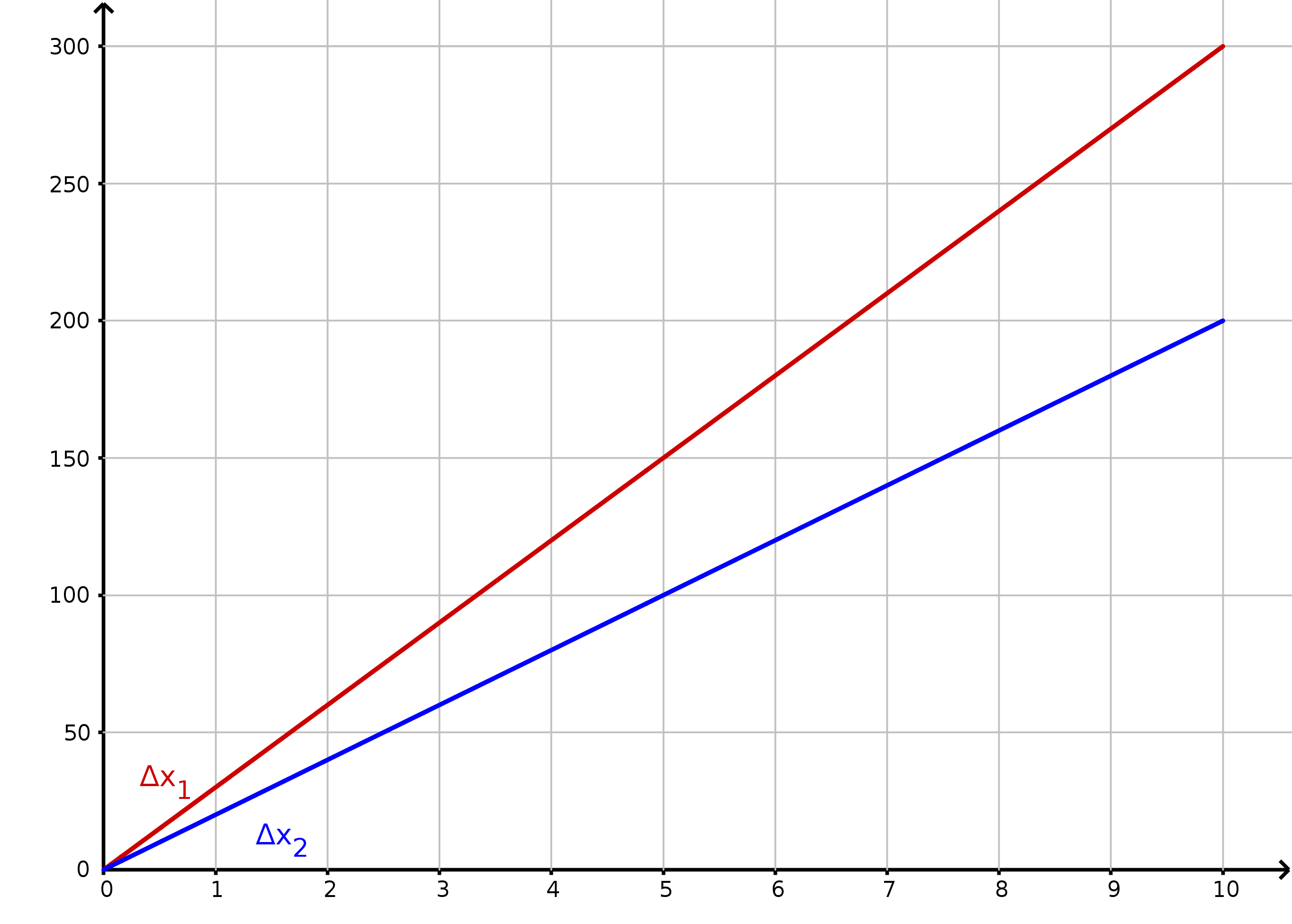
Θέμα Δ
Δ1
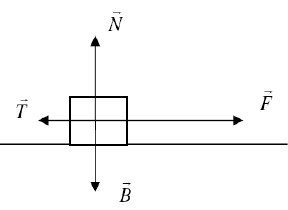
Περιβάλλον για το κιβώτιο αποτελούν η γη, το οριζόντιο επίπεδο και ο άνθρωπος που ασκεί σταθερή δύναμη F.
\[B = m \cdot g \Rightarrow B = 20N\] \[ΣF_y = 0 \Rightarrow N - B = 0 \Rightarrow N = 20N\] \[T = μ \cdot N \Rightarrow T = 10N\] \[F = 20N\]Δ2
\[α = \frac{ΣF_x}{m} \Rightarrow α = \frac{F - T}{m} \Rightarrow α = 5 \frac{m}{s^2}\]Δ3
\[\underline {α) τρόπος}\]Το κιβώτιο εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση άρα για την μετατόπιση και την ταχύτητα ισχύουν οι σχέσεις:
\[x = υ_ο \cdot t + \frac{1}{2} \cdot α \cdot t^2 \Rightarrow 10 = 0 + \frac{1}{2} \cdot 5 \cdot t^2 \Rightarrow t^2 = 4 \Rightarrow t = 2sec\] \[υ = υ_ο + α \cdot t \Rightarrow υ = 0 + 5 \cdot 2 \Rightarrow υ = 10 \frac{m}{sec}\] \[\underline {β) τρόπος}\] \[ΔΚ = ΣW \Rightarrow K_{ΤΕΛ} - Κ_{ΑΡΧ} = W_B + W_F + W_N + W_T\] \[\frac{1}{2} \cdot m \cdot υ^2 - 0 = 0 + F \cdot x + 0 - T \cdot x \Rightarrow υ^2 = 100 \Rightarrow υ = 10 \frac{m}{sec}\]Δ4
\[\underline {α) τρόπος}\] \[α = \frac{ΣF_x}{m} \Rightarrow α = \frac{T}{m} \Rightarrow α = 5 \frac{m}{s^2}\]Το κιβώτιο εκτελεί ευθύγραμμη ομαλά επιβραδυνόμενη κίνηση άρα για την ταχύτητα και την μετατόπιση ισχύουν οι σχέσεις:
\[υ = υ_ο - α \cdot t \Rightarrow 0 = 10 - 5 \cdot t \Rightarrow t = 2sec\] \[x = υ_ο \cdot t - \frac{1}{2} \cdot α \cdot t^2 \Rightarrow x = 10 \cdot 2 - \frac{1}{2} \cdot 5 \cdot 2^2 \Rightarrow x = 10m\] \[\underline {β) τρόπος}\] \[ΔΚ = ΣW \Rightarrow K_{ΤΕΛ} - Κ_{ΑΡΧ} = W_B + W_N + W_T\] \[0 - \frac{1}{2} \cdot m \cdot υ_o^2 = 0 + 0 - T \cdot x \Rightarrow - \frac{1}{2} \cdot 2 \cdot 10^2 = - 10 \cdot x \Rightarrow x = 10m\]blog comments powered by Disqus