Επαναληπτικές 2025
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(δ\)
Α2 - \(α\)
Α3 - \(β\)
Α4 - \(γ\)
Α5: \(Λ - Σ - Σ - Λ - Σ\)
Θέμα Β
Β1 - \((i)\)
Φωτοηλεκτρική εξίσωση του Einstein, για φωτόνια με μήκος κύματος \(λ\).
\[K_{max}= \frac{h\cdot c}{λ} - φ\]Φωτοηλεκτρική εξίσωση του Einstein, για φωτόνια με μήκος κύματος \(λ'=\frac{λ}{3}\).
\[K'_{max}= \frac{h\cdot c}{\frac{λ}{3}} - φ\]Αφαιρούμε τις εξισώσεις κατά μέλη
\[10eV-2eV = 2 \cdot \frac{h \cdot c}{λ} \Rightarrow \frac{h\cdot c}{λ} = 4eV\]Προσθέτουμε τις εξισώσεις κατά μέλη
\[10eV+2eV = 4 \cdot \frac{h \cdot c}{λ} -2 \cdot φ \Rightarrow 12eV =4 \cdot \frac{h \cdot c}{λ} -2 \cdot φ\]Αντικαθιστώντας το \(\frac{h\cdot c}{λ}\) έχουμε
\[12eV=4 \cdot 4eV - 2 \cdot φ \Rightarrow φ=2 eV\]άρα σωστό το (i)
Β2 - \((ii)\)
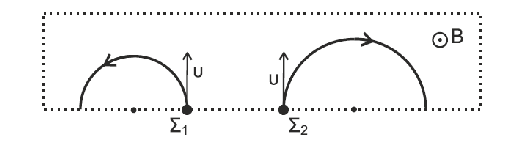
Η δύναμη που δέχεται το κάθε φορτισμένο σωματίδιο από το μαγνητικό πεδίο είναι κάθετη στην ταχύτητα.
Για το σωματίδιο \(Σ_1\)
\[F_{μαγν} = F_{κεντρ} \Rightarrow |q| \cdot υ \cdot B = \frac{m \cdot υ^2}{R} \Rightarrow υ = \frac{|q| \cdot B \cdot R}{m}\]H περίοδος περιφοράς είναι
\[T= \frac{2π\cdot R}{υ} \Rightarrow T = \frac{2π\cdot R}{\frac{q \cdot B \cdot R}{m}} \Rightarrow T = \frac{2π \cdot m}{q \cdot B}\]Η τροχιά είναι ημικυκλική άρα για τη χρονική διάρκεια παραμονής του σωματιδίου \(Σ_1\) στο μαγνητικό πεδίο ισχύει
\[Δt_1 = \frac{T_1}{2} \Rightarrow Δt_1 = \frac{\frac{2π \cdot m}{q \cdot B}}{2} \Rightarrow Δt_1 = \frac{π \cdot m}{q \cdot B}\]Παρόμοια η χρονική διάρκεια παραμονής του σωματιδίου \(Σ_2\) (\(m_2=4m\) και \(q_2=2q\)) στο μαγνητικό πεδίο είναι:
\[Δt_2 = \frac{2π \cdot m}{q \cdot B}\]Οπότε η χρονική διαφορά εξόδου είναι
\[Δt = Δt_2 - Δt_1 \Rightarrow Δt = \frac{2π \cdot m}{q \cdot B} - \frac{π \cdot m}{q \cdot B} \Rightarrow Δt = \frac{π \cdot m}{q \cdot B}\]άρα σωστό το (ii)
Β3 - \((iii)\)
Κύλιση χωρίς ολισθηση
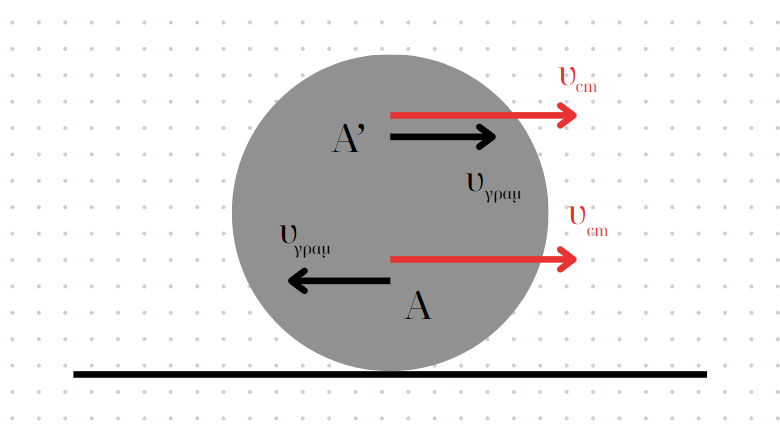
σημείο Α:
\[\vec{υ_Α}_{min} = \vec{υ_{cm}} + \vec{υ_{γρα}} \Rightarrow υ_{Αmin} = υ_{cm} - υ_{γρα} \Rightarrow \frac{υ_{cm}}{4} = υ_{cm} - υ_{γρα} \Rightarrow υ_{γρα} = \frac{3}{4} \cdot υ_{cm}\]σημείο Α’
\[\vec{υ_Α'}_{max} = \vec{υ_{cm}} + \vec{υ_{γρα}} \Rightarrow υ_{Α'max} = υ_{cm} + υ_{γρα} \Rightarrow υ_{Α'max} = υ_{cm} + \frac{3}{4} \cdot υ_{cm} \Rightarrow υ_{Α'max} = \frac{7}{4} \cdot υ_{cm}\]άρα σωστό το (iii)
Θέμα Γ
Γ1-\((10)\)
α) Νόμος των Biot - Savart
\[ΔΒ = \frac{μ_0}{4π} \cdot \frac{I\cdot Δ\ell}{r^2} \cdot ημθ\] \[B = \sum_{Γ}^{Δ}ΔΒ = \frac{μ_0}{4π} \cdot \frac{I}{α^2} \sum_{Γ}^{Δ}Δ \ell \cdot ημ90^0 = \frac{μ_0}{4π} \cdot \frac{I \cdot π \cdot α}{α^2} = \frac{μ_ο \cdot I}{4α}\] \[Ι = \frac{E}{R_A + r} = 4A\] \[B = 2π \cdot 10^{-5} T\]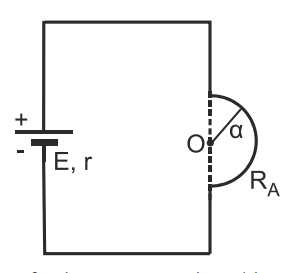
Η φορά των γραμμών του μαγνητικού πεδίου στο σημείο $Ο$ είναι από τον αναγνώστη προς τη σελίδα.
β) Ρυθμός μεταβολής θερμότητας
\[\frac{ΔQ_{θερμ}}{Δt} = P_A = I^2 \cdot R_A\] \[\frac{ΔQ_{θερμ}}{Δt} = P_r = I^2 \cdot r\] \[\frac{P_A}{P_r} = 2\]Γ2-\((15)\)
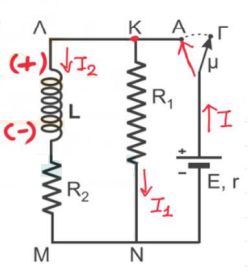
α) O μεταγωγός μετακινείται από τη θέση $Γ$ στη θέση $Α$ και τα ρεύματα έχουν σταθεροποιηθεί.
\[U_B = \frac{1}{2} \cdot L \cdot I_2^2\] \[\frac{ΔΙ_2}{Δt} = 0\] \[V_L = - L \cdot \frac{dI_2}{dt}=0\] \[I = \frac{E}{\frac{R_1 \cdot R_2}{R_1+R_2} + r } \Rightarrow I = 6A\] \[V_{KN} = E - I \cdot r \Rightarrow V_{KN} = 12V\] \[I_2 = \frac{V_{KN}}{R_2} \Rightarrow I_2 = 3A\] \[U_B = \frac{1}{2} \cdot L \cdot I_2^2 \Rightarrow U_B = 0,9J\]β) για τη χρονική στιγμή $t_1$
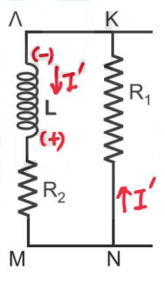
το $i_L$ μειώνεται άρα η πολικότητα στο πηνίο φαίνεται στο σχήμα.
Ο δεύτερος κανόνας του Kirchhoff
\[|V_L| -i_L \cdot R_2 - i_L \cdot R_1 = 0 \Rightarrow |V_L| = 24V\] \[E_{αυτ} = -L \cdot \frac{dI}{dt} = V_L \Rightarrow \frac{dI}{dt} = -120 \frac{A}{s}\]Θέμα Δ
Δ1-\((10)\)
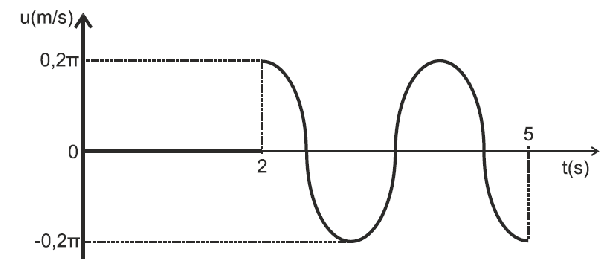
α) για το σώμα μάζας $m$ που εκτελεί απλή αρμονική ταλάντωση ισχύει:
\[Δt = 6 \cdot \frac{T}{4} \Rightarrow 5-2 = 6 \cdot \frac{T}{4} \Rightarrow T=2s\] \[D=m\cdot ω^2 = 0,2 \cdot π^2 \Rightarrow D=2 \frac{N}{m}\]β) από το σχήμα γνωρίζουμε τη μέγιστη ταχύτητα οπότε
\[υ_{mac} = ω \cdot A \Rightarrow A = \frac{υ_{mac}}{ω} \Rightarrow A = 0,2m\]Τη χρονική στιγμή $t_1=2,5s$ ισχύει $υ=0$ και $x_1=+A$ αφού αμέσως μετά η ταχύτητα είναι αρνητική.
Τη χρονική στιγμή $t_2=3,5s$ ισχύει $υ=0$ και $x_2=-A$ αφού αμέσως μετά η ταχύτητα είναι θετική.
Άρα το σώμα μάζας $m$ διήνυσε συνολικά απόσταση
\[d=2\cdot A = 0,4m\]Οπότε η μέση ταχύτητα είναι
\[υ_{μεση} = \frac{d}{Δt} = \frac{0,4}{3,5-2,5}= 0,4 \frac{m}{s}\]Δ2-\((15)\)
α) εξίσωση κύματος \(y = A \cdot ημ(\frac{2πt}{T} - \frac{2πx}{λ} ) \quad (S.I.)\)
\[υ_δ = \frac{x_A}{t_A} \Rightarrow 1 = \frac{x_A}{2} \Rightarrow x_A = 2m\] \[ω = \frac{2π}{Τ} = \frac{2π}{2} = π \frac{rad}{s}\] \[υ_δ = \frac{λ}{Τ} \Rightarrow 1 = \frac{λ}{2} \Rightarrow λ = 2m\] \[υ_{max} = ω \cdot A \Rightarrow 0,2 π = π \cdot A \Rightarrow A = 0,2m\]Οπότε η εξίσωση του κύματος είναι
\[y = 0,2 \cdot ημ(\frac{2π \cdot t}{2} - \frac{2π \cdot x}{2}) \Rightarrow y = 0,2 \cdot ημ(π \cdot t -π \cdot x) \quad (S.I.)\]Για τη χρονική στιγμή $t_1$
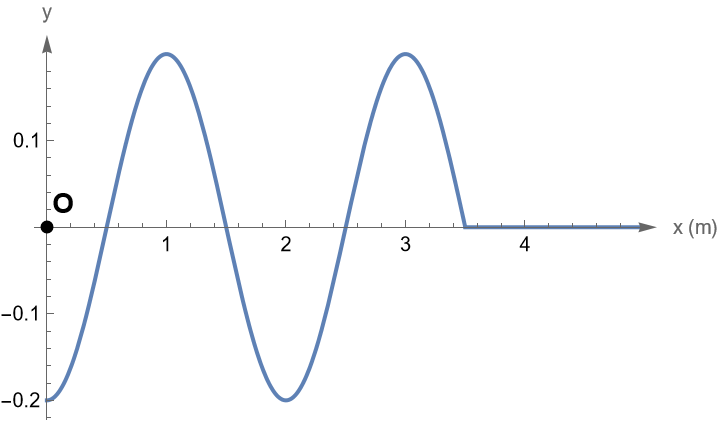
Δηλαδή για $α<0$ πρέπει $y>0$ δηλαδή
$0,5m < x < 1,5m$ και $2,5m < x < 3,5m$
β)
\[y_1 = 0,2 \cdot ημ(π \cdot t - π \cdot x) \quad (S.I.)\] \[y_2 = 0,2 \cdot ημ(π \cdot t + π \cdot x + φ_0) \quad (S.I.)\]Την χρονική στιγμή \(t_0=0\), \(x_1 = 4,5m\), και \(φ_2=0\).
\[φ_2 = π \cdot t + π \cdot x + φ_0 \Rightarrow 0 = π \cdot 0 + π \cdot 4,5 + φ_0 \Rightarrow φ_0=-4,5 rad\]οπότε η εξίσωση κύματος για το δεύτερο κύμα είναι
\[y_2 = 0,2 \cdot ημ(π \cdot t + π \cdot x - 4,5 π) \quad (S.I.)\]Τα δύο κύματα $y_1$ και $y_2$ έχουν διαδοθεί στο διάστημα $0 \le x \le 4,5m$ την χρονική στιγμή $t_1 = \frac{x_1}{υ_δ}=4,5s$$
Τα κύματα συμβάλλουν
\[y = y_1 + y_2 = 0,2 \cdot ημ(π \cdot t - π \cdot x) + 0,2 \cdot ημ(π \cdot t + π \cdot x - 4,5 π)\]με χρήση της γνωστής τριγωνομετρικής ταυτότητας
\[y= 0,4 \cdot συν(\frac{φ_2 - φ_1}{2}) \cdot ημ(\frac{φ_1+φ_2}{2} )\]και μετά τις πράξεις
\[y = 0,4 \cdot συν(π \cdot x - 2,25π) \cdot ημ (π \cdot t - 2,25 π) \quad (S.I.)\]$0 \le x \le 4,5m$, είναι ακίνητα για όσα ισχύει
\[0,4 \cdot συν(π \cdot x - 2,25π) =0 \Rightarrow π \cdot x - 2,25π = k \cdot π + \frac{π}{2} \Rightarrow x = k + 2,75\]Όπου k ακέραιος, οπότε
\[0 \le k + 2,75 \le 4,5m -2,75 \le k \le 1,75\]Άρα για το k οι τιμές είναι $-2, -1, 0, 1$.
Οπότε οι ζητούμενες θέσεις είναι
\[0,75m \quad 1,75m \quad 2,75m \quad 3,75m\]Μπορείτε να εκτυπώσετε τα θέματα και τις λύσεις σε μορφή pdf
blog comments powered by Disqus