Μοριοδότηση 2024
Ενδεικτικές απαντήσεις και από γραπτά μαθητών
Θέμα Α
Α1 - \(δ\)
Α2 - \(γ\)
Α3 - \(γ\)
Α4 - \(β\)
Α5: \(Σ - Λ - Σ - Σ - Λ\)
Θέμα Β
Β1 - \((ii)\)
Εξίσωση Wien \(λ_{max} \cdot T = σταθ\)
\[φ_1=2π\cdot(10^{15}t-\frac{10^7}{3}x) \quad (S.I.)\]Από τη σχέση \(φ=\frac{2πt}{T}-\frac{2πx}{λ}\) έχουμε
\[\frac{2πt}{T_1}= 2π\cdot10^{15}t \Rightarrow T_1=10^{-15} sec \Rightarrow f_1=10^{15} Hz\] \[\frac{2πx}{λ_{1max}} = 2π \cdot \frac{10^7}{3}x \Rightarrow λ_{1max}= 3 \cdot 10^{-7} m\] \[c=λ_{1max} \cdot f_1 = 3 \cdot 10^8 \frac{m}{s}\]Από τα δεδομένα \(Τ_2 = 2\cdot T_1\)
Άρα από την εξίσωση Wien
\[λ_{2max} \cdot T_2 = λ_{1max} \cdot T_1 \Rightarrow λ_{2max} = \frac{λ_{1max}}{2} \Rightarrow λ_{2max} = \frac{3}{2} \cdot 10^{-7} m\] \[c=λ_{2max} \cdot f_2 \Rightarrow f_2=2 \cdot 10^{15} Hz\] \[T_2 = \frac{1}{f_2} \Rightarrow T_2 = 0,5 \cdot 10^{-15} sec\] \[φ_2=\frac{2πt}{T_2}-\frac{2πx}{λ_2} \Rightarrow φ_2 = 2π\cdot (2 \cdot 10^{15}t-\frac{2}{3}\cdot 10^7 x) \quad (S.I.)\]άρα σωστό το (ii)
Β2 - \((i)\)
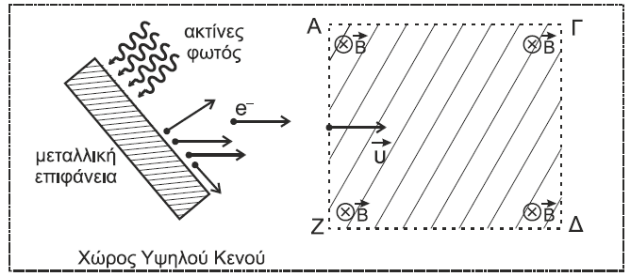
Κυκλική κίνηση φωτοηλεκτρονίου
\[F_{μαγνητική} = F_{κεντρομόλο} \Rightarrow B \cdot υ \cdot e = \frac{m \cdot υ^2}{r} \Rightarrow r = \frac{m \cdot υ}{B \cdot e}\] \[L = m \cdot υ \cdot r = m \cdot υ \cdot \frac{m \cdot υ}{B \cdot e} = \frac{m}{e \cdot B} \cdot m \cdot υ^2 = \frac{m \cdot 2K}{e \cdot B}\]και λύνοντας ως προς την κινητική ενέργεια \(Κ = \frac{L \cdot e \cdot B}{2m}\)
Όμως η κινητική ενέργεια συνδέεται με το έργο εξαγωγής
\[K = \frac{hc}{λ} - \phi \Rightarrow \frac{L_1 \cdot e \cdot B}{2m} = \frac{hc}{λ_1} - \phi\]Παρόμοια για το δεύτερο πείραμα
\[\frac{L_2 \cdot e \cdot B}{2m} = \frac{hc}{λ_2} - \phi \Rightarrow \frac{5L_1 \cdot e \cdot B}{2m} = \frac{hc}{\frac{λ_1}{2}} - \phi\]Διαιρώντας τις δύο τελευταίες σχέσεις προκύπτει:
\[\frac{1}{5} = \frac{\frac{hc}{λ_1}-\phi}{\frac{2hc}{λ_1}}\]και μετά τις πράξεις
\[\phi = \frac{3}{4} \cdot \frac{hc}{λ_1} = \frac{3}{4} \cdot \frac{1250}{375} \Rightarrow \phi = 2.5 eV\]άρα σωστό το (i)
Β3 - \(α(ii), β(i)\)
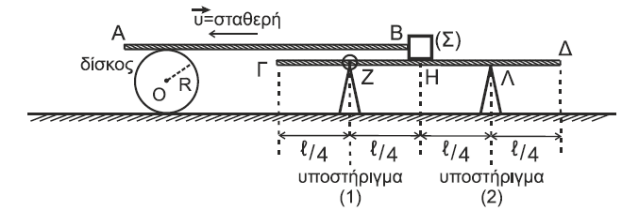
α) Στο σχήμα δείχνονται οι δυνάμεις που ασκούνται στη δοκό \(ΓΔ\) και στο σώμα \(Σ\) τη χρονική στιγμή \(t_1\).
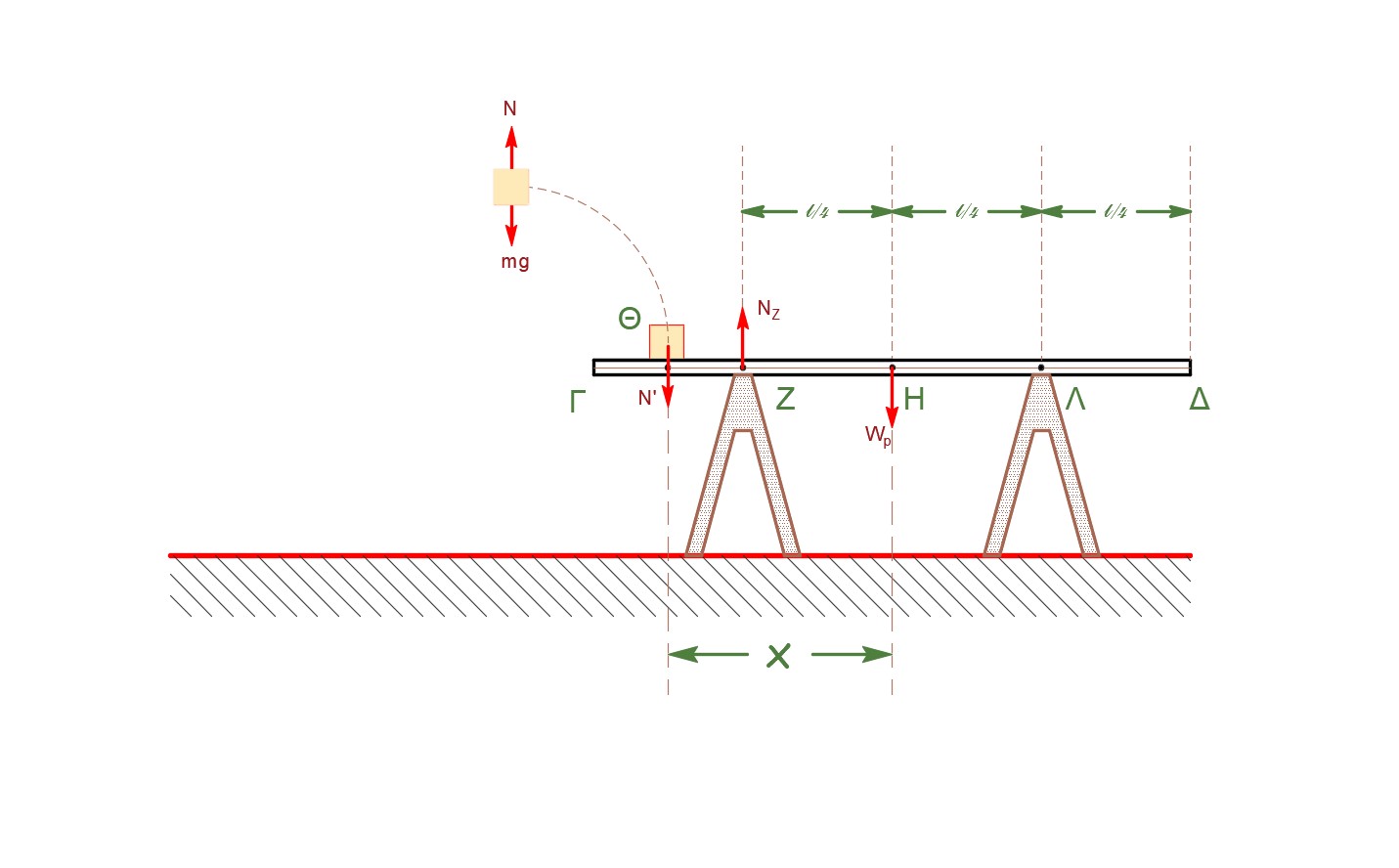
Για τη δοκό \(ΓΔ\) ισχύει:
\[W_ρ = Μ \cdot g \Rightarrow W_ρ = \frac{m \cdot g}{2}\]Το σώμα \(Σ\) ισορροπεί στον κατακόρυφο άξονα οπότε:
\[Ν - m \cdot g =0 \Rightarrow N= m \cdot g\]Λόγω του \(3^{ου}\) Νόμου του Νεύτωνα ισχύει
\[Ν' = Ν = m \cdot g\]Το σύστημα δοκός \(ΓΔ\) και σώμα \(Σ\) ισορροπεί οριακά αφού η δοκός μόλις που χάνει οριακά την επαφή της με την κορυφή του υποστηρίγματος (2), άρα
\[Στ_{(Ζ)} = 0 \Rightarrow N'(x-\frac{l}{4})-W_ρ \cdot \frac{l}{4} = 0 \Rightarrow m \cdot g (x-\frac{l}{4})=\frac{m \cdot g}{2} \cdot \frac{l}{4}\]και μετά τις πράξεις \(x = \frac{3l}{8}\)
άρα σωστό το ii
β) Έστω \(Ε\) σημείο της ράβδου \(ΑΒ\) που είναι σε επαφή με τον δίσκο και \(Ζ\) το σημείο του δίσκου που είναι σε επαφή με την ράβδο όπως δείχνεται στο σχήμα:
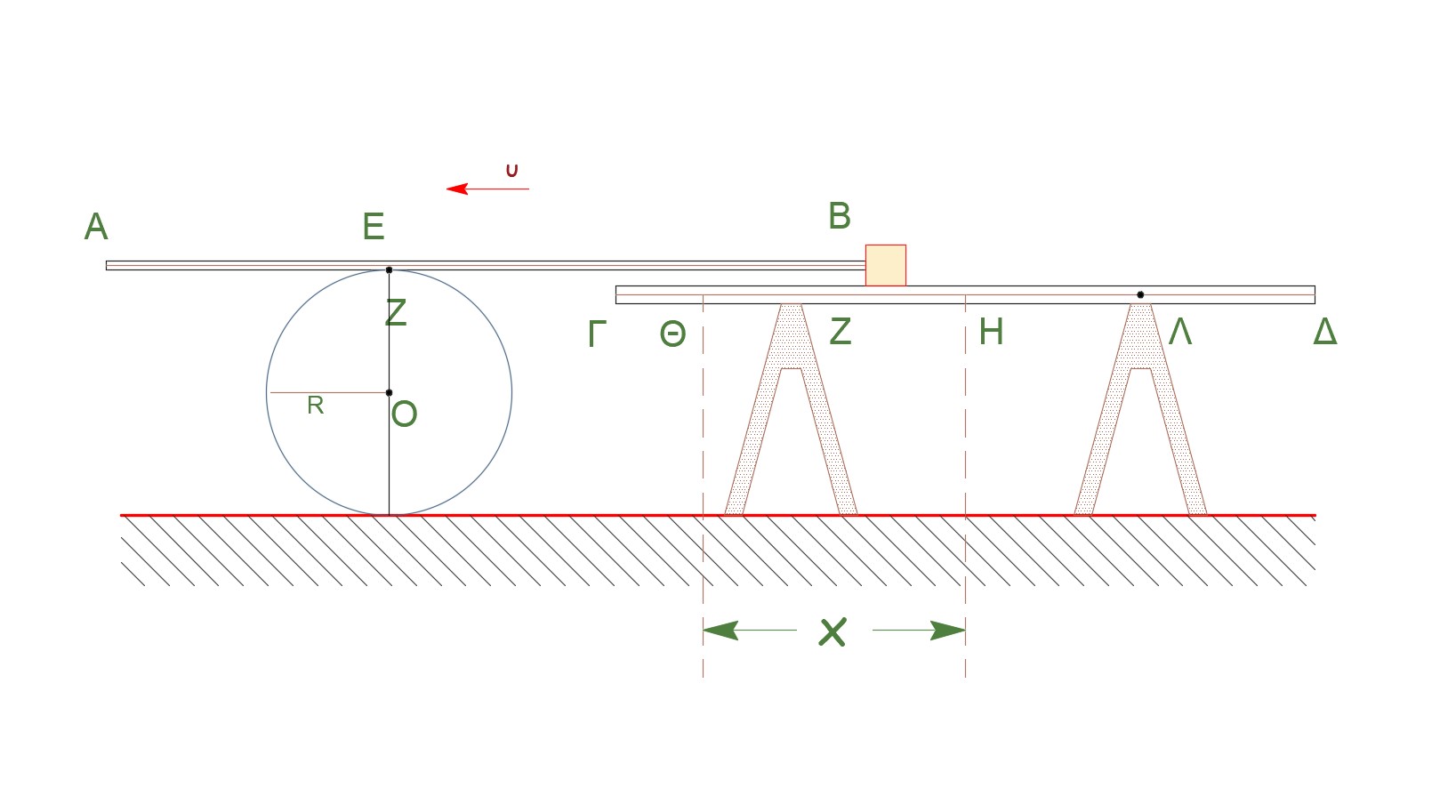
Ο δίσκος κάνει κύλιση χωρίς ολίσθηση άρα \(Δx_{(O)} = Δθ \cdot R\), άρα
\[Δx_B = 2 \cdot Δx_O \Rightarrow \frac{3l}{8} = 2 \cdot Δx_O \Rightarrow Δx_O = \frac{3l}{16}\]άρα σωστό το i
Θέμα Γ
Γ1-\((7)\)
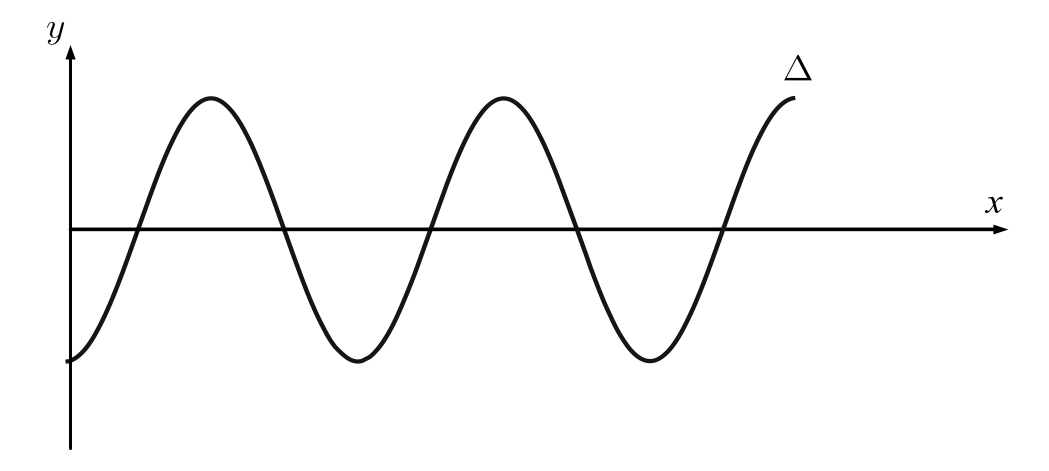
Άρα το \(Ο\) έχει διανύσει απόσταση \(4Α+4Α+2Α = 2 \Rightarrow A=0,2m\)
Γ2-\((5)\)
\[y_Δ = Α \cdot ημωΔt\] \[Δt = t - t_{ΕΚ(Δ)} = t - \frac{x_Δ}{υ_Δ}\] \[y_Δ = A \cdot ημ \frac{2π}{Τ}(t - \frac{x_Δ}{υ_Δ}) = A ημ 2π(\frac{t}{T} - \frac{x_Δ}{υ_Δ \cdot T} )\] \[υ_Δ = \frac{λ}{Τ} \Rightarrow λ = υ_Δ \cdot T\] \[y_Δ = Α ημ 2π(\frac{t}{T} - \frac{x_Δ}{λ} )\]Γ3-\((7)\)
Για το υλικό σημείο \(Δ\)
\[y_Δ = \begin{cases} 0 \quad 0 \le t < 5 sec \\\ 0,2 ημ (πt - 5π) \quad 5 sec \le t \end{cases}\] \[υ_Δ = ω Α συν φ_Δ = \frac{π}{5} συν(πt - 5π)\] \[υ_Δ = \begin{cases} 0 \quad 0 \le t < 5 sec \\\ \frac{π}{5} συν(πt - 5π) \quad 5 sec \le t \le 8 sec \end{cases}\] \[Δt_{ταλ(Δ)} = 8 - 5 = 3sec\]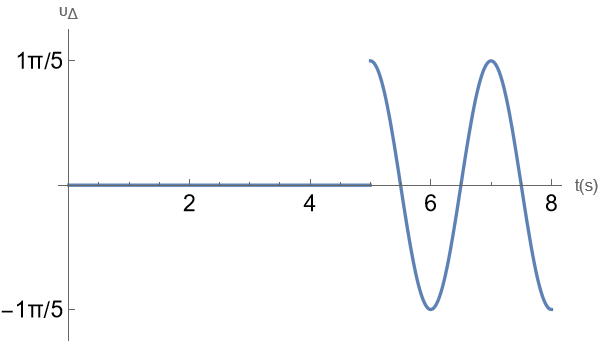
Γ4-\((6)\)
Για τα σημεία \(Ο\) και \(Δ\) για κάθε χρονική στιγμή ισχύει
\(y_{(O)} = y_{(Δ)}\) και \(υ_{ταλ(Ο)} = υ_{ταλ(Δ)}\)
\[Α ημφ_{(Ο)} = Α ημφ_{(Δ)} \begin{cases} φ_{(Ο)} = 2kπ + φ_{(Δ)} \\\ φ_{(Ο)} = 2kπ + π - φ_{(Δ)} \end{cases}\] \[Αω συνφ_{(Ο)} = Αω συνφ_{(Δ)} \begin{cases} φ_{(Ο)} = 2kπ + φ_{(Δ)} \\\ φ_{(Ο)} = 2kπ - φ_{(Δ)} \end{cases}\]Οι εξισώσεις συναληθεύουν για
\[φ_{(Ο)} = 2kπ + φ_{(Δ)} \Rightarrow φ_{(Ο)} - φ_{(Δ)} = 2kπ \Rightarrow \frac{2π \cdot (ΟΔ)}{λ'} = 2kπ\]Και επειδή τα σημεία είναι διαδοχικά θα πρέπει \(k=1\), άρα
\[\frac{2π \cdot (ΟΔ)}{λ'} = 2π \Rightarrow (ΟΔ) = λ' \Rightarrow λ'= 2,5 m\]Αφού δεν αλλάζει το ελαστικό μέσο η ταχύτητα παραμένει ίδια άρα
\[υ_Δ = λ' \cdot f' \Rightarrow 0,5 = 2,5 \cdot f' \Rightarrow f' = 0,2 Hz\] \[Δf = f' - f = 0,2 - 0,5 \Rightarrow Δf = -0,3 Hz\]Άρα η συχνότητα μειώθηκε κατά \(0,3 Hz\).
Θέμα Δ
Δ1-\((5)\)
Από τη θέση (1) που είναι ακραία θέση προς τη θέση (2) που είναι η Θ.Φ.Μ. θέση του φυσικού μήκους του ελατηρίου το σώμα \(Σ\) δέχεται τη δύναμη του ελατηρίου \(F_{ελ}\) και την δύναμη \(F_{επαφ}\) από τη μεταλλική ράβδο και επιταχύνεται. Η μεταλλική ράβδος επιταχύνεται μαζί με το σώμα \(Σ\) αφού δέχεται τη δύναμη \(F_{επαφ}'\) (δράση - αντίδραση). Οι δυνάμεις δείχνονται στα σχήματα που ακολουθούν.
Για το σώμα \(Σ\)
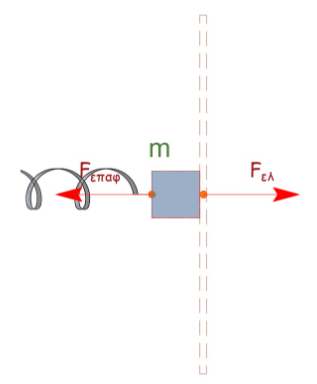
Για τη μεταλλική ράβδο
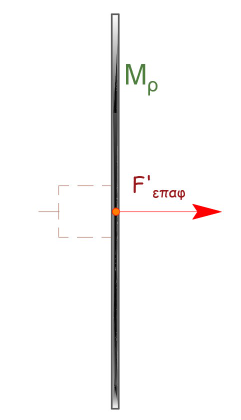
Από τη θέση (2) Θ.Φ.Μ η \(F_{ελ}\) στο σώμα \(Σ\) είναι προς τα αριστερά και το επιβραδύνει, ενώ η μεταλλική ράβδος συνεχίζει να κινείται με σταθερή ταχύτητα \(υ = υ_{max}\). Άρα χάνεται η επαφή και καταργείται η \(F_{επαφ}\) στη Θ.Φ.Μ.
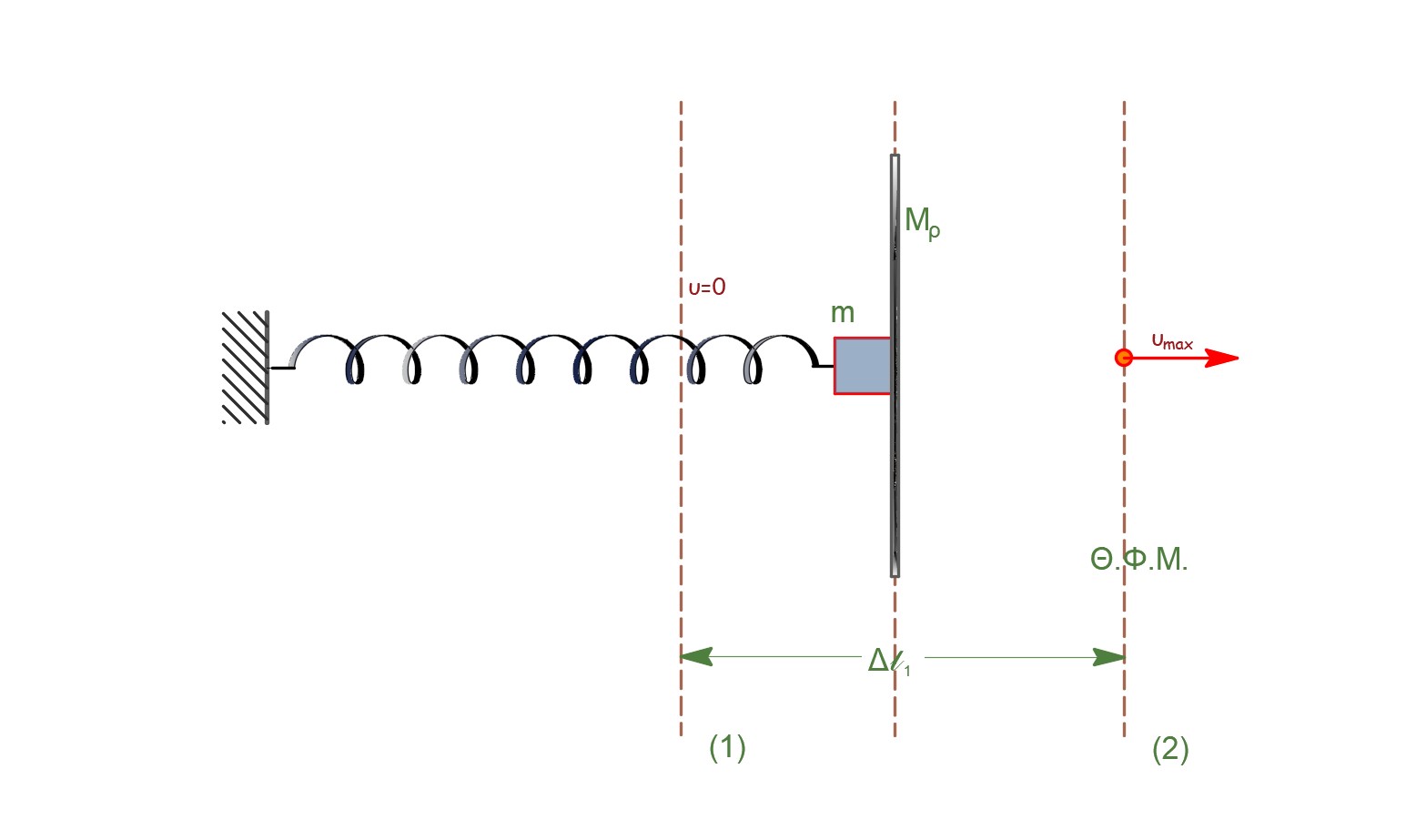
Για το συσσωμάτωμα σώμα - ράβδος που εκτελεί απλή αρμονική ταλάντωση ισχύει:
\[D = k = (m+M_ρ)\cdot ω^2 \Rightarrow ω = \sqrt \frac{k}{m+M_ρ}\]Και μετά τις πράξεις \(ω = 2,5 \frac{rad}{s}\).
H θέση φυσικού μήκους του ελατηρίου είναι και θέση ισορροπίας της ταλάντωσης
\[Δl = A =0,4 m\] \[υ_{max} = A \cdot ω \Rightarrow υ_{max} = 1 \frac{m}{s}\]Μετά τη θέση (2) το σώμα \(Σ\) εκτελεί νέα Α.Α.Τ. με
\[D = k = m\cdot ω'^2 \Rightarrow ω' = \sqrt \frac{k}{m}\]Και μετά τις πράξεις \(ω' = 5 \frac{rad}{s}\).
\[υ_{max} = υ_{max}' \Rightarrow υ_{max}'=Α' \cdot ω' \Rightarrow Α' = 0,2 m\]Δ2-\((4)\)
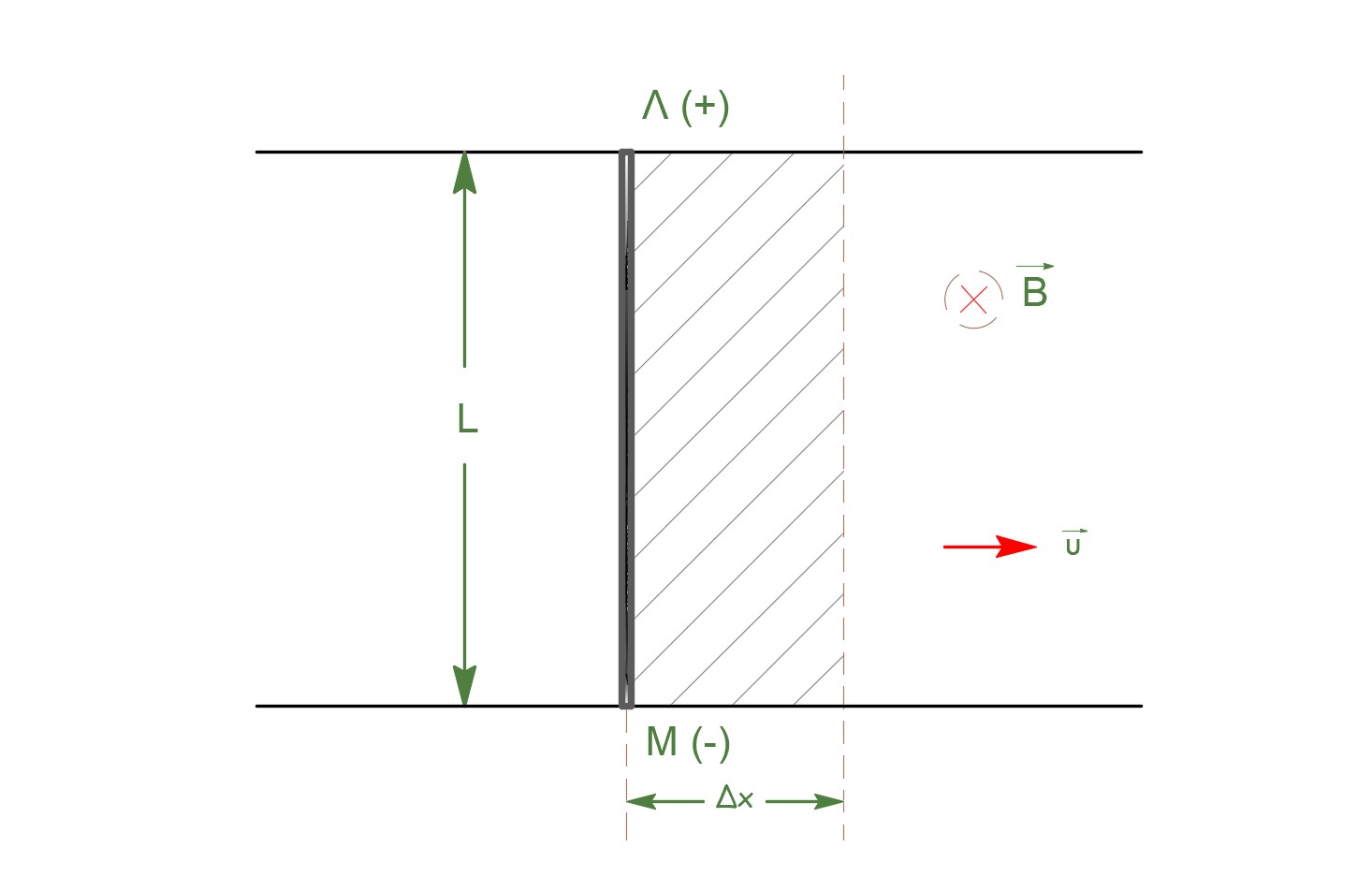
Σύμφωνα με τον κανόνα του δεξιού χεριού, κάθε ηλεκτρόνιο της ράβδου δέχεται δύναμη Lorentz \(F_{μαγν} = q \cdot υ \cdot B\) με φορά προς το \(Μ\).
\[Ε_{επ} = \frac{ΔΦ}{Δt} = \frac{B \cdot ΔS}{Δt} = \frac{B \cdot Δx \cdot L}{Δt} = B \cdot υ \cdot L\]Δ3-\((4)\)
Για τη χρονική στιγμή \(t_1\)
\[E_{επ1} = Β \cdot υ \cdot L = Β \cdot υ_{max} \cdot L \Rightarrow E_{επ1} = 1Volt\]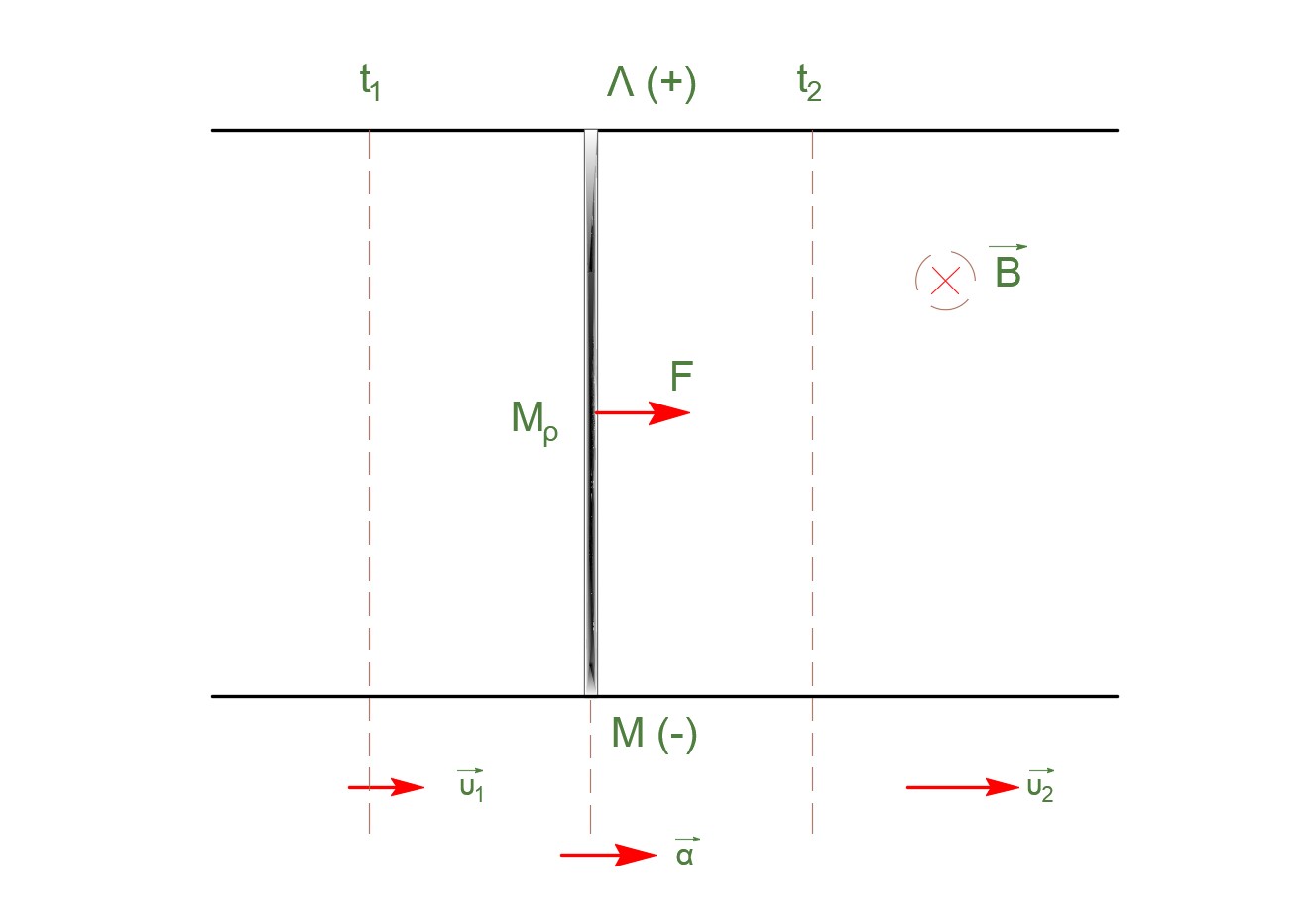
Για τη χρονική διάρκεια από \(t_1\) έως \(t_2\) η μεταλλική ράβδος δεν διαρρέεται από ρεύμα και εκτελεί ευθύγραμμη ομαλά επιταχυνόμενη κίνηση.
\[F = m \cdot α \Rightarrow α = \frac{F}{m} \Rightarrow α = 2,5 \frac{m}{s^2}\] \[υ_2 = υ_1 + α \cdot (t_2 - t_1) \Rightarrow υ_2 = 6 \frac{m}{s}\]Δ4-\((6)\)
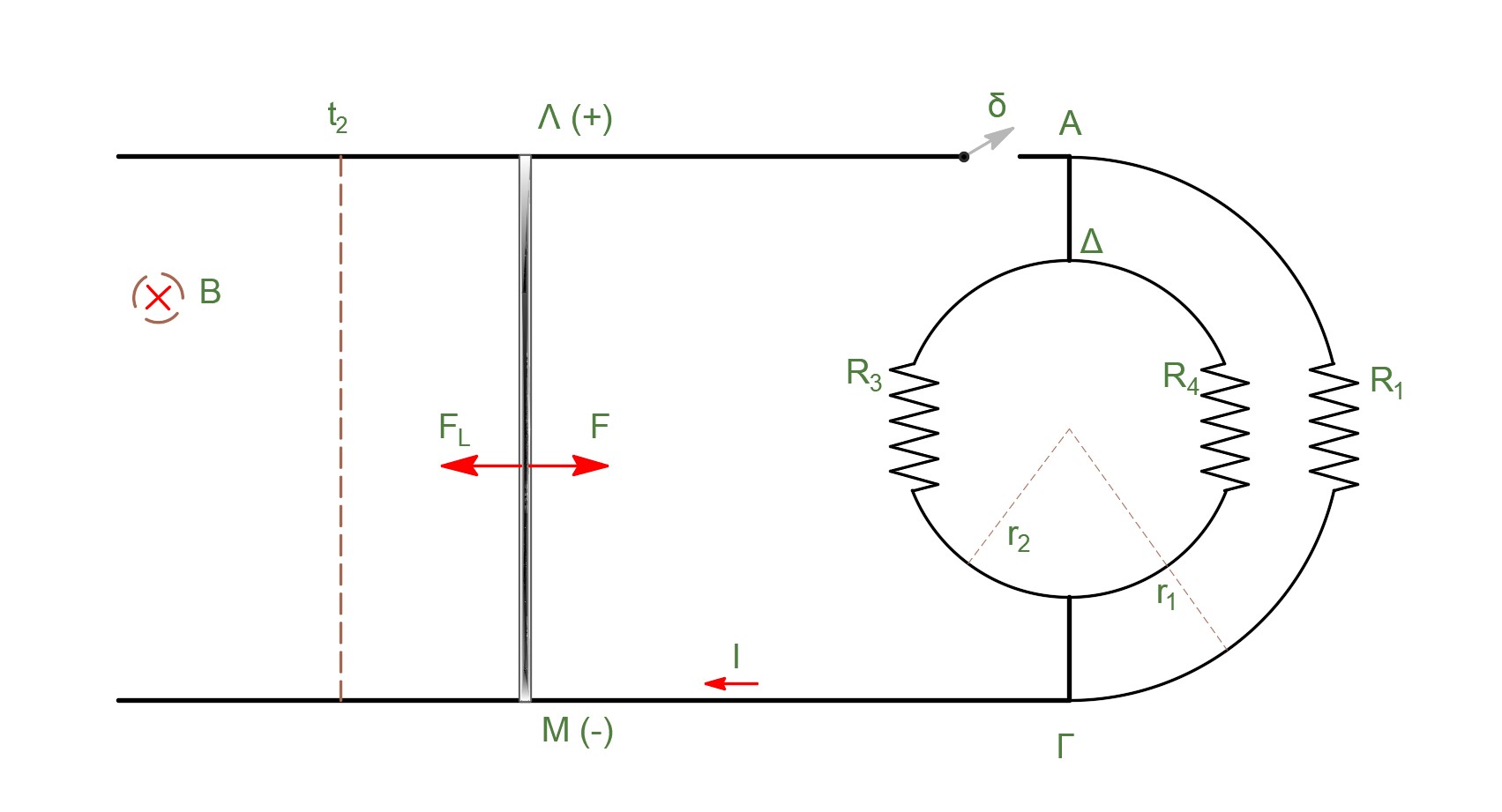
Για τη χρονική στιγμή \(t_2\)
\[E_{επ2} = Β \cdot υ_2 \cdot L \Rightarrow E_{επ2} = 6Volt\]Για την ωμική αντίσταση του ημικυκλικού και του κυκλικού αγωγού ισχύει \(R = ρ \cdot \frac{l}{S}\)
\[R_2 = ρ \cdot \frac{2 \cdot π \cdot r_2}{S}\]και επειδή τα ημικύκλια \(ΔΝΖ\) και \(ΔΘΖ\) έχουν το ίδιο μήκος
\[R_3 = ρ \cdot \frac{\frac{2 \cdot π \cdot r_2}{2} }{S}\] \[R_4 = ρ \cdot \frac{\frac{2 \cdot π \cdot r_2}{2} }{S} = R_3\] \[\frac{R_2}{R_3} =2 \Rightarrow R_3 = \frac{R_2}{2} \Rightarrow R_3 = R_4 = 5Ω\]Για την παράλληλη σύνδεση αντιστατών ισχύει
\[\frac{1}{R_{34}} = \frac{1}{R_3} + \frac{1}{R_4} \Rightarrow R_{34} = 2,5Ω\]ενώ για τη συνολική αντίσταση
\[\frac{1}{R_{εξ}} = \frac{1}{R_{34}} + \frac{1}{R_1} \Rightarrow R_{εξ} = 2Ω\]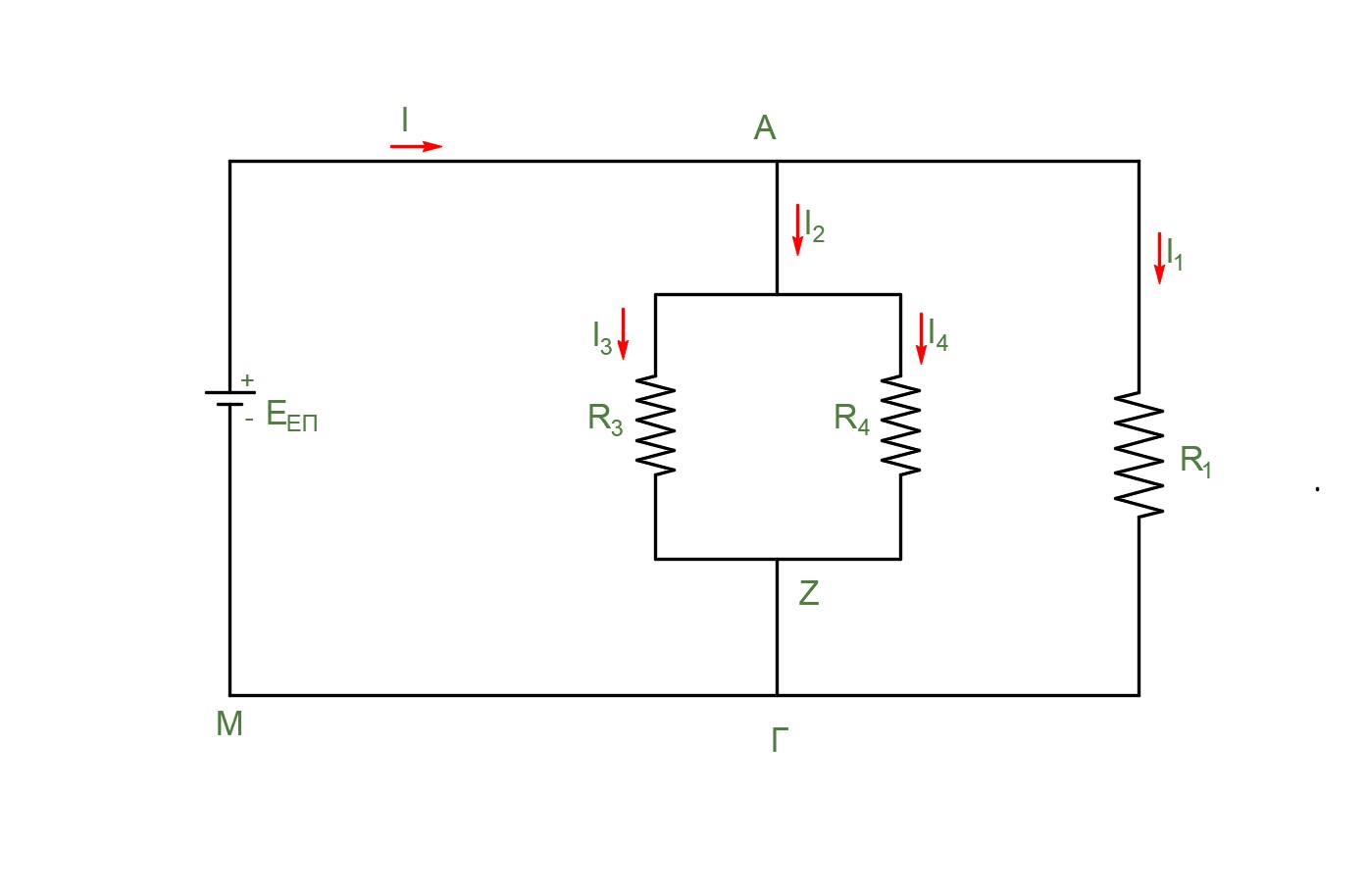
Από το νόμο του Ohm για τη χρονική στιγμή \(t_2\)
\[I = \frac{E_{επ}}{R_{εξ}} \Rightarrow I = 3 A\] \[F_L = B \cdot I \cdot L \Rightarrow F_L = 3N\] \[ΣF = F - F_L \Rightarrow ΣF = 0\]Άρα από τη χρονική στιγμή \(t_2\) και μετά η μεταλλική ράβδος \(ΛΜ\) εκτελεί ευθύγραμμη ομαλή κίνηση και διαρρέεται από σταθερό ρεύμα \(I = 3A\).
Ο ημικυκλικός αγωγός \(ΔΘΖ\) διαρρέεται από ρεύμα \(Ι_3\)
\[Ι_3 = \frac{V_{ΑΓ}}{R_3} = \frac{E_{επ}}{R_3} \Rightarrow I_3 = 1,2 A\]Ο ημικυκλικός αγωγός \(ΔNΖ\) διαρρέεται από ρεύμα \(Ι_4\)
\[Ι_4 = \frac{V_{ΑΓ}}{R_4} = \frac{E_{επ}}{R_4} \Rightarrow I_4 = 1,2 A\]Ο ημικυκλικός αγωγός \(ΑΗΓ\) διαρρέεται από ρεύμα \(Ι_1\)
\[Ι_1 = \frac{V_{ΑΓ}}{R_1} = \frac{E_{επ}}{R_1} \Rightarrow I_1 = 0,6 A\]Δ5-\((6)\)
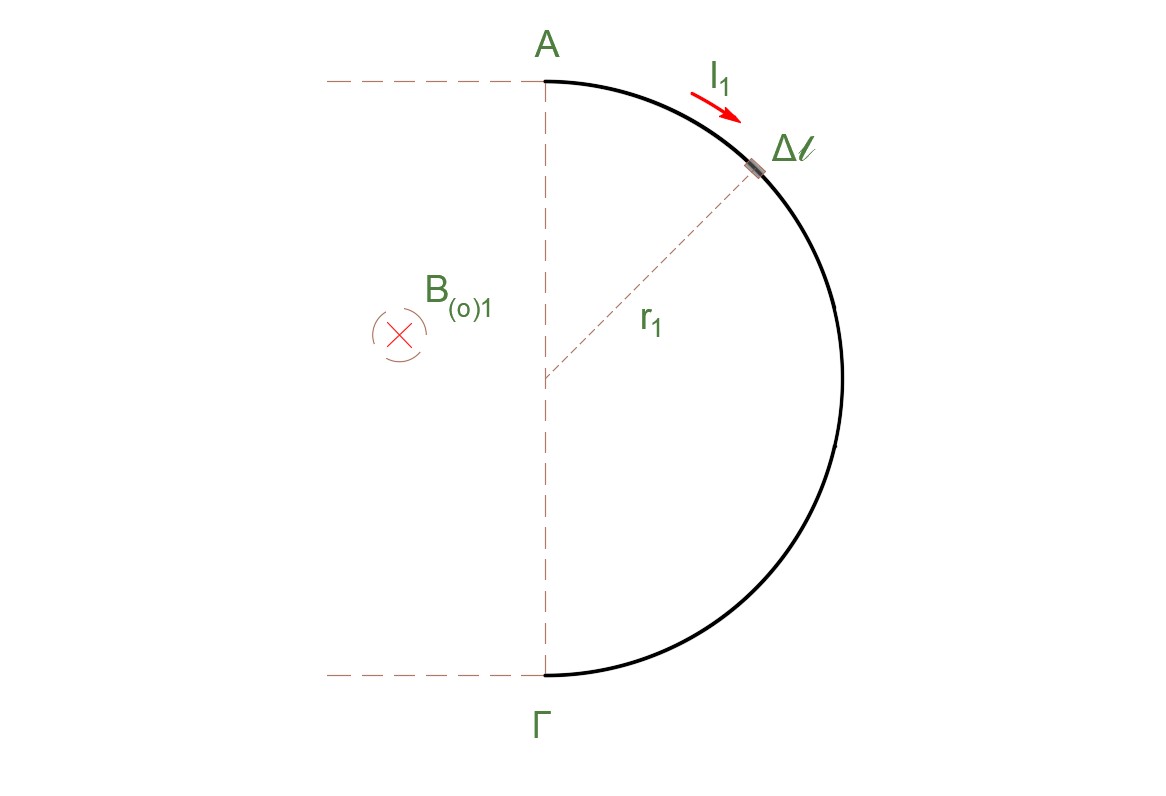
Σύμφωνα με το νόμο των Biot και Savart
\[B_{(O)1} = \frac{μ_0}{4π} \cdot \frac{I_1}{r_1^2}(Δl_1+Δl_2+...) = \frac{μ_0}{4π} \cdot \frac{I_1 \cdot π \cdot r_1}{r_1^2} = \frac{μ_0 \cdot Ι_1}{4r_1}\]και μετά τις πράξεις \(B_{(O)1} = 1,2 π \cdot 10^{-7} T\)
Για τον κυκλικό αγωγό
\[B_{(O)34} = B_{(O)4} - B_{(O)3} = \frac{μ_0 \cdot I_4}{4 \cdot r_2} - \frac{μ_0 \cdot I_3}{4 \cdot r_2} =0\]Άρα το συνολικό μαγνητικό πεδίο στο κέντρο \(Ο\) είναι
\[Β_{ολ} = B_{(O)1} = 1,2 π \cdot 10^{-7} T\]Μπορείτε να εκτυπώσετε τα θέματα και τις λύσεις σε μορφή pdf
Ο κώδικας σε Mathematica για τη δημιουργία της γραφικής παράστασης στο θέμα \(Γ_3\)
f[t_] := Piecewise[ { {0, 0<=t<5}, {π/5*Cos[π*t - 5 π], 5<=t<=8} }]
Plot[f[t], {t, 0, 8},
PlotRange -> {All, {-π/4, π/4}},
AxesLabel -> {"t(s)", Subscript[υ, Δ]},
Ticks -> {Automatic, Table[{k Pi/5, Row[{k, "π/5"}]}, {k, -4, 4}]},
TicksStyle -> Directive[FontSize -> 14]]
blog comments powered by Disqus