Σύνθεση ταλαντώσεων

θέμα Δ

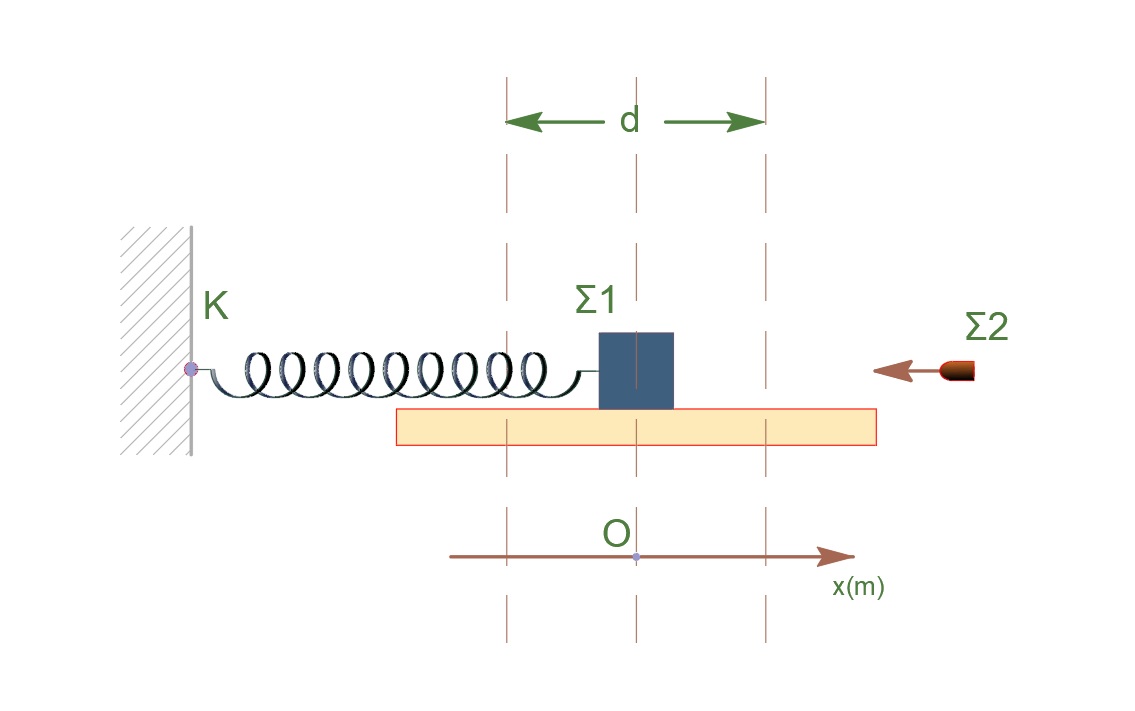
Σώμα \(Σ_1\) μάζας \(m = 50 \quad g\) ισορροπεί ακίνητο πάνω σε οριζόντια βάση, δεμένο στην άκρη ενός οριζόντιου ελατηρίου, η άλλη άκρη του οποίου είναι στερεωμένη σε ακίνητο σημείo \(K\) κατακόρυφου τοίχου όπως φαίνεται στο σχήμα. Δεύτερο σώμα \(Σ_2\) ίσης μάζας που κινείται στη διεύθυνση του άξονα του ελατηρίου συγκρούεται με τον σώμα \(Σ_1\) και σφηνώνεται ακαριαία σε αυτό. Το συσσωμάτωμα \(Σ\) που προκύπτει μπορεί να κινείται χωρίς τριβές και εκτελεί απλή αρμονική ταλάντωση μεταξύ δύο ακραίων θέσεων που απέχουν απόσταση \(d = 2 \quad cm\). Ο ελάχιστος χρόνος μετάβασης του συσσωματώματος από τη μια ακραία θέση στην άλλη είναι \(Δt_1 = 0.1π \quad s\).

Δ1. Να γράψετε τη χρονική εξίσωση της απομάκρυνσης \(x_1 = f(t)\) του συσσωματώματος \(Σ\), γύρω από τη θέση ισορροπίας του \(Ο\) Θεωρώντας ότι τη χρονική στιγμή μηδέν το συσσωμάτωμα βρίσκεται στο σημείο \(Ο\) και κινείται κατά την αρνητική φορά.

Δ2 Να υπολογίσετε την ενέργεια που μετατρέπεται σε θερμότητα κατα την πλαστική κρούση.

Στη συνέχεια αφαιρείται το ελατήριο από το συσσωμάτωμα και αντικαθίσταται η οριζόντια λεία επιφάνεια της βάσης με νέα βάση για την οποία ο συντελεστής στατικής τριβής μεταξύ του συσσωματώματος \(Σ\) και της βάσης είναι \(μ_σ = \sqrt3\). Με κατάλληλο μηχανισμό η νέα βάση εκτελεί απλή αρμονική ταλάντωση σε διεύθυνση ίδια με την προηγούμενη και γύρω από την ίδια θέση ισορροπίας \(Ο\) με πλάτος και συχνότητα ταλάντωσης \(Α_2 = \sqrt3 \quad cm\) και \(f_2 = \frac{5}{π} \quad Hz\) αντίστοιχα.

Δ3. Αν γνωρίζετε ότι τη χρονική στιγμή \(t_o = 0\) η νέα βάση βρίσκεται στην ακραία θέση της και ο ρυθμός μεταβολής της ταχύτητάς της είναι αρνητικός, να δείξετε ότι το συσσωμάτωμα \(Σ\) δεν ολισθαίνει για όσο χρόνο κινείται η βάση και να γράψετε τη χρονική εξίσωση της απομάκρυνσης \(x_2 = f(t)\) του συσσωματώματος \(Σ\) γύρω από τη θέση ισορροπίας \(Ο\).

Δ4. Να γράψετε τη χρονική εξίσωση της ταχύτητας \(υ = f(t)\) της σύνθετης ταλάντωσης που εκτελεί το συσσωμάτωμα \(Σ\) γύρω από τη ίδια θέση ισορροπίας του \(Ο\) στην ίδια διεύθυνση, αν θεωρήσουμε ότι μπορεί να κάνει ταυτόχρονα τις δύο προηγούμενες αρμονικές ταλαντώσεις \(x_1 = f(t)\) και \(x_2 = f(t)\).

Δ5 Όταν η απομάκρυνση του συσσωματώματος \(Σ\) από τη θέση ισορροπίας \(Ο\) λόγω της πρώτης ταλάντωσης είναι \(x_1 = 0.5 \quad cm\) και η ταχύτητά του είναι θετική, να βρείτε το ρυθμό μεταβολής της ορμής του συσσωματώματος για τη σύνθετη ταλάντωση.