Ευθύγραμμος αγωγός - Εξήγηση
Η οριζόντια μεταλλική ράβδος \(ΑΓ\) μήκους \(L\), έχει ωμική αντίσταση \(R_1=\frac{R}{2}\) και κινείται με σταθερή ταχύτητα \(υ\), πάνω στους οριζόντιους μεταλλικούς οδηγούς, αμελητέας αντίστασης, \(ΖX_1\) και \(ΔX_2\), των οποίων τα άκρα \(Ζ\), \(Δ\) συνδέονται με σύρμα αντίστασης \(R\).
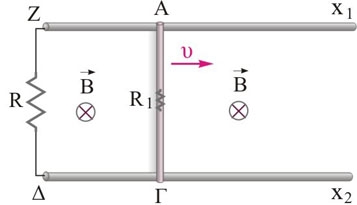
Στο χώρο υπάρχει κατακόρυφο ομογενές μαγνητικό πεδίο, με φορά όπως δείχνεται στο σχήμα (κάτοψη). Η διαφορά δυναμικού \(V_{ΖΔ}\), είναι
- $$V_{ΖΔ} = BυL$$
- $$V_{ΖΔ} = \frac{2}{3} \cdot BυL$$
- $$V_{ΖΔ} = \frac{1}{3} \cdot BυL$$
Να επιλέξετε τη σωστή απάντηση, να σχεδιάσετε την φορά του επαγωγικού ρεύματος και να δικαιολογήσετε την επιλογή σας.
Οι δύο μεταλλικοί οδηγοί, η ράβδος και ο αντιστάτης αποτελούν ένα κλειστό πλαίσιο από το οποίο διέρχεται μαγνητική ροή \(Φ=ΒS\), όπου \(S\) το εμβαδόν του σχηματιζόμενου πλαισίου. Καθώς η ράβδος κινείται, μεταβάλλεται η επιφάνεια \(S\) με συνέπεια να αυξάνεται η μαγνητική ροή που διέρχεται από το πλαίσιο και να εμφανίζεται επαγωγική τάση. Αν σε χρονική διάρκεια \(dt\) η ράβδος έχει μετατοπιστεί κατά \(dx\), τότε η επαγωγική τάση που εμφανίζεται στο πλαίσιο είναι
\[E_{επ} = |-\frac{dΦ}{dt}| \Rightarrow E_{επ} = |-\frac{B \cdot dS}{dt}| \Rightarrow E_{επ} = |-\frac{B \cdot L \cdot dx}{dt}|\]όμως γνωρίζουμε για την ταχύτητα ότι \(υ=\frac{dx}{dt}\) οπότε
\[E_{επ} = ΒυL\]Αφού στο κλειστό κύκλωμα \(ΑΖΔΓΑ\) δημιουργείται \(ΗΕΔ\) από επαγωγή, το κύκλωμα αυτό διαρρέεται από επαγωγικό ρεύμα με φορά όπως αυτή του σχήματος.
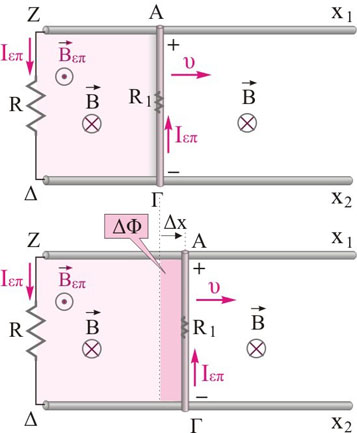
α) τρόπος
Σύμφωνα με τον κανόνα του \(Lenz\), η φορά του επαγωγικού ρεύματος είναι τέτοια, ώστε να αντιστέκεται στην αιτία που το προκαλεί. Η αιτία που προκαλεί την αύξηση της μαγνητικής ροής είναι η κίνηση της ράβδου με φορά προς τα δεξιά. Συνεπώς το επαγωγικό ρεύμα έχει φορά τέτοια, ώστε η δύναμη Laplace που δέχεται η ράβδος να αντιστέκεται στην κίνησή του (σύμφωνα με τον κανόνα του δεξιού χεριού, φορά προς τα αριστερά).
β) τρόπος
Αφού η μαγνητική ροή που διέρχεται από το κύκλωμα \(ΑΖΔΓΑ\) αυξάνεται, το επαγωγικό ρεύμα δημιουργεί δικό του μαγνητικό πεδίο που έχει σύμφωνα με τον κανόνα του \(Lenz\) αντίθετη φορά από αυτό που ήδη υπάρχει (δηλαδή δημιουργεί μαγνητικό πεδίο με φορά από την σελίδα προς τον αναγνώστη). Για να συμβαίνει αυτό, πρέπει, σύμφωνα με τον κανόνα του δεξιού χεριού, το επαγωγικό ρεύμα να έχει φορά αντίθετη από αυτήν της φοράς κίνησης των δεικτών του ρολογιού.
γ) τρόπος
Στην ράβδο υπάρχουν ελεύθερα ηλεκτρόνια το οποία συμμετέχουν στην προς τα δεξιά κίνηση της. Αυτά τα αρνητικά φορτία κινούνται με ταχύτητα \(υ\) κάθετη στις δυναμικές γραμμές του ομογενούς μαγνητικού πεδίου. Το μαγνητικο πεδίο ασκεί δύναμη \((Lorentz)\) που είναι κάθετη στο επίπεδο που ορίζεται από την ταχύτητα και την διεύθυνση του πεδίου και η φορά της δίνεται από τον κανόνα του δεξιού χεριού. Η δύναμη αυτή προκαλεί την κίνηση των ελεύθερων ηλεκτρονίων προς το άκρο \(Γ\). Έτσι δημιουργείται συσσώρευση αρνητικού φορτίου στο άκρο \(Γ\) και πλεόνασμα θετικού φορτίου στο άκρο \(Α\). Τα φορτία αυτά δημιουργούν στο χώρο του αγωγού ομογενές ηλεκτρικό πεδίο ένασης \(Ε\) με φορά από το \(Α\) προς το \(Γ\). Τα ελεύθερα ηλεκτρόνια δέχονται τώρα μια δύναμη \(F_{ηλ} = E \cdot |q|\) αντίθετης φοράς από την μαγνητική. Όσο η δύναμη Lorentz είναι μεγαλύτερη από την ηλεκτρική η συσσώρευση φορτίου συνεχίζεται με όλο και μικρότερο ρυθμό. Έτσι η ένταση του ηλεκτρικού πεδίου αυξάνεται και σε πολύ λίγο χρόνο τα μέτρα των δυο δυνάμεων γίνονται ίσα.
\[Ε \cdot |q| = B \cdot υ \cdot |q| \Rightarrow E = B \cdot υ\]Τότε παύει η μετακίνηση φορτίου και το σημείο \(Α\) βρίσκεται σε υψηλότερο δυναμικό από το \(Γ\). Η διαφορά δυναμικού μεταξύ των άκρων του αγωγού είναι
\[Ε = \frac{Ε_{επ}}{L} \Rightarrow Ε_{επ} = Ε \cdot L \Rightarrow E_{επ} = Β \cdot υ \cdot L\]Το κλειστό κύκλωμα \(ΑΖΔΓΑ\) διαρρέεται από επαγωγικό ρεύμα του οποίου η ένταση είναι
\[Ι_{επ} = \frac{Ε_{επ}}{R_{ολ}} = \frac{BυL}{R+R_1} = \frac{BυL}{R+\frac{R}{2}}=\frac{2BυL}{3R}\]α) τρόπος
H διαφορά δυναμικού \(V_{ΖΔ}\) στα άκρα της αντίστασης \(R\), σύμφωνα με τον νόμο του \(Ohm\) είναι
\[V_{ΖΔ} = Ι_{επ} \cdot R = \frac{2BυL}{3R} \cdot R = \frac{2}{3}\cdot BυL\]β) τρόπος
H διαφορά δυναμικού \(V_{ΖΔ}\) στα άκρα της αντίστασης \(R\) είναι ίση με τον πολική τάση στα άκρα της πηγής \(Ε_{επ}\)
\[V_{ΖΔ} = V_{ΑΓ} = Ε_{επ} - Ι_{επ} \cdot R_1 = B \cdot υ \cdot L - \frac{2BυL}{3R} \cdot \frac{R}{2}\]και μετά τις πράξεις
\[V_{ΖΔ} = \frac{2}{3}\cdot BυL\]Άρα σωστό το \(2\).
blog comments powered by Disqus