Προσομοίωση 2020

ΘΕΜΑ A Στις ερωτήσεις $Α_1-Α_4$ να γράψετε στο τετράδιό σας τον αριθμό της ερώτησης και δίπλα το γράμμα που αντιστοιχεί στη φράση η οποία συμπληρώνει σωστά την ημιτελή πρόταση.

$A_1$

Ένα σωληνοειδές έχει αντίσταση $R$, τροφοδοτείται από τάση $V$ διαρρέεται από ρεύμα $Ι$ και έχει στο εσωτερικό του μαγνητική επαγωγή $Β$. Αν το κόψουμε στη μέση και πάρουμε το πρώτο μισό και το τροφοδοτήσουμε με την ίδια τάση $V$ τότε η νέα μαγνητική επαγωγή $Β΄$ στο εσωτερικό του νέου σωληνοειδούς είναι:

$$ B $$
$$ 2 \cdot B $$
$$ \frac{B}{2} $$
$$ \frac{B}{4} $$

$A_2$

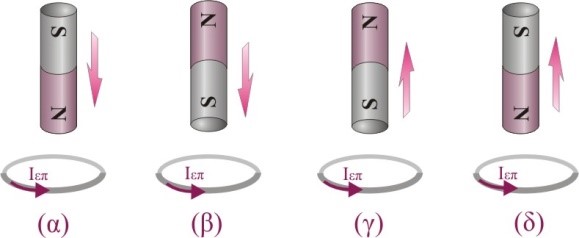
σχήμα

Ο ευθύγραμμος μαγνήτης του σχήματος περνά μέσα από το μεταλλικό δακτυλίδι. Στο δακτυλίδι εμφανίζεται επαγωγικό ρεύμα του οποίου η φορά δίνεται σωστά στις περιπτώσεις

(α) και (γ)
(α) και (β)
(γ) και (β)
(γ) και (δ)

$A_3$ Σε μια φθίνουσα ταλάντωση, οι μονάδες της σταθεράς απόσβεσης στο $(S.I.)$ είναι:

$$ kg \cdot s $$
$$ \frac{s}{kg} $$
$$ \frac{kg}{s} $$
$$ \frac{kg}{s^2} $$

$A_4$

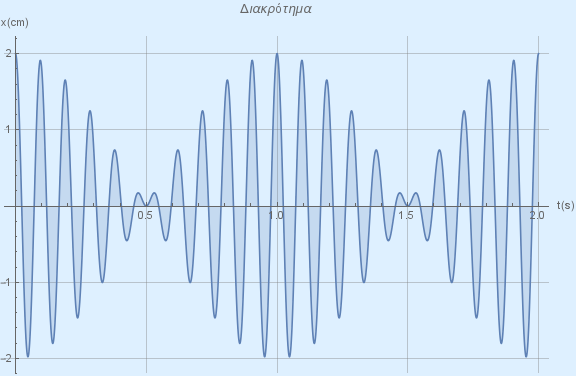
σχήμα

Στο σχήμα φαίνεται η γραφική παράσταση της απομάκρυνσης σε συνάρτηση με το χρόνο μιας σύνθετης κίνησης που παρουσιάζει διακροτήματα. Η περίοδος των διακροτημάτων είναι:

$$ 0.5 s $$
$$ 1 s $$
$$ 1.5 s $$
$$ 2 s $$

$A_5$

Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.

α. Σε μια εξαναγκασμένη ταλάντωση το πλάτος της ταλάντωσης εξαρτάται από τη συχνότητα του διεγέρτη και τη σταθερά απόσβεσης $b$

β. Σώμα $Σ_1$ μάζας $m_1$ που κινείται προς τη θετική κατεύθυνση συγκρούεται κεντρικά και ελαστικά με δεύτερο ακίνητο σώμα $Σ_2$ μάζας $m_2$. Η ποσότητα της κινητικής ενέργειας που έχει μεταφερθεί από τo σώμα $Σ_1$ στo σώμα $Σ_2$ μετά την κρούση γίνεται μέγιστη όταν $m_1 > m_2$

γ. Σώμα $Σ_1$ μάζας $m_1$ που κινείται προς τη θετική κατεύθυνση συγκρούεται κεντρικά και ελαστικά με δεύτερο ακίνητο σώμα $Σ_2$ μάζας $m_2$. Το σώμα $Σ_2$ αποκτά την μεγαλύτερη ορμή όταν έχει πολύ μεγαλύτερη μάζα από το Α.

δ. Σε μια φθίνουσα ταλάντωση, στην οποία η αντιτιθέμενη δύναμη είναι ανάλογη της ταχύτητας, ο λόγος δύο διαδοχικών μεγίστων απομακρύνσεων προς την ίδια κατεύθυνση διατηρείται σταθερός.

ε. Σκέδαση ονομάζεται κάθε φαινόμενο του μικρόκοσμου στο οποίο τα «συγκρουόμενα» σωματίδια αλληλεπιδρούν με σχετικά μικρές δυνάμεις για πολύ μικρό χρόνο.

ΘΕΜΑ Β

$Β_1$

Ένα σώμα εκτελεί κίνηση που προέρχεται από τη σύνθεση δύο απλών αρμονικών ταλαντώσεων που γίνονται πάνω στην ίδια ευθεία, γύρω από την ίδια θέση ισορροπίας και οι απομακρύνσεις των οποίων από τη θέση ισορροπίας τους περιγράφονται από τις σχέσεις:

\[x_1 = 0.04 \cdot ημ10 \cdot t \quad S.I.\] \[x_2 = 0.03 \cdot ημ(10 \cdot t + π) \quad S.I.\]

Κάποια χρονική στιγμή, η απομάκρυνση λόγω της πρώτης ταλάντωσης είναι $x_1 = 3 cm$. Την ίδια χρονική στιγμή η απομάκρυνση της σύνθετης ταλάντωσης είναι:

$$ x = 0.75 cm $$
$$ x = 1.00 cm $$
$$ x = -2.25 cm $$

$Β_2$

Ένας αντιστάτης διαρρέεται από εναλλασσόμενο ρέυμα πλάτους $Ι$ και περιόδου $Τ$. Η θερμότητα $Q$ που αναπτύσσεται στον αντιστάτη σε χρόνο $Δt = 1.5 T$ είναι:

$$ Q = \frac{I^2 \cdot R \cdot T}{2} $$
$$ Q = \frac{3 \cdot I^2 \cdot R \cdot T}{2} $$
$$ Q = \frac{3 \cdot I^2 \cdot R \cdot T}{4} $$
τίποτα από τα παραπάνω

Να επιλέξετε την σωστή απάντηση και να δικαιολογήσετε την επιλογή σας.

$Β_3$

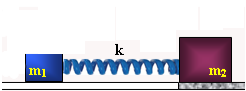
σχήμα

Σώμα $Α$ έχει μάζα $m_1$ και επάνω του είναι στερεωμένο ιδανικό ελατήριο σταθεράς $k$ όπως φαίνεται στο σχήμα. Το σώμα $Α$ κινείται με ταχύτητα $υ$ και συγκρούεται κεντρικά με ακίνητο σώμα $Β$ μάζας $m_2 = 4 \cdot m_1$. Κατά την διάρκεια του φαινομένου δεν υπάρχει απώλεια μηχανικής ενέργειας. Tη στιγμή που το ελατήριο αποκτά τη μέγιστη συσπείρωση το ποσοστό της ενέργειας του σώματος $Α$ που μεταφέρθηκε στο σώμα $Β$ είναι:

$Β_4$

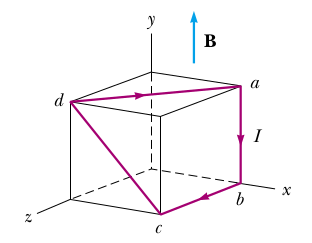
σχήμα

Στο σχήμα φαίνεται ένας κύβος ακμής $40cm$. Τέσσερα σύρματα ab, bc, cd και da σχηματίζουν κλειστό βρόχο ο οποίος διαρρέεται από ρεύμα $Ι=5A$.Το σύστημα βρίσκεται σε ΟΜΠ έντασης $B=0.02T$ που είναι κατακόρυφο προς τα πάνω.

Α. Η δύναμη Laplace στον αγωγό ab έχει μέτρο:

$$ 0N $$
$$ 0.04N $$
$$ 0.04 \sqrt2 N $$
τίποτα από τα παραπάνω

Β. Η δύναμη Laplace στον αγωγό bc έχει μέτρο:

$$ 0N $$
$$ 0.04N $$
$$ 0.04 \sqrt2 N $$
τίποτα από τα παραπάνω

Γ. Η δύναμη Laplace στον αγωγό cd έχει μέτρο:

$$ 0N $$
$$ 0.04N $$
$$ 0.04 \sqrt2 N $$
τίποτα από τα παραπάνω

Δ. Η δύναμη Laplace στον αγωγό da έχει μέτρο:

$$ 0N $$
$$ 0.04N $$
$$ 0.04 \sqrt2 N $$
τίποτα από τα παραπάνω

Να επιλέξετε τις σωστές απαντήσεις και να δικαιολογήσετε τις επιλογές σας.

ΘΕΜΑ Γ

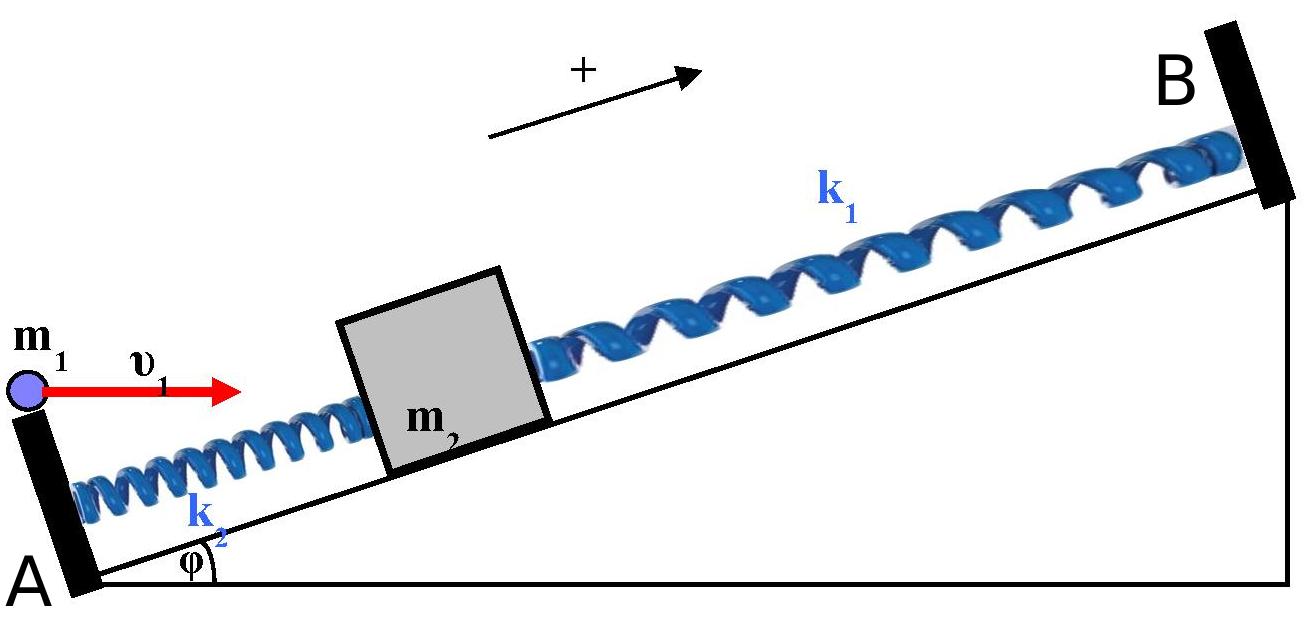
σχήμα

Λείο κεκλιμένο επίπεδο έχει γωνία κλίσης $φ=30^ο$. Στα σημεία $Α$ και $Β$ στερεώνουμε τα άκρα δύο ιδανικών ελατηρίων με σταθερές $k_1=60 \frac{Ν}{m}$ και $k_2 = 40 \frac{Ν}{m}$ αντίστοιχα. Οι θέσεις του φυσικού μήκους των ελατηρίων ταυτίζονται. Σώμα $Σ_1$ μάζας $m_1 = 2 kg$ κινείται οριζόντια με ταχύτητα $υ_1 = 2 \frac{m}{s}$ και συγκρούεται πλαστικά και ακαριαία με σώμα $Σ_2$ ίσης μάζας $m_2=m_1$ που ισορροπεί δεμένο στα ιδανικά ελατήρια, όπως φαίνεται στο σχήμα. Μετά την πλαστική κρούση το συσσωμάτωμα δεν αναπηδά.

$Γ_1$ Να αποδείξετε ότι το συσσωμάτωμα εκτελεί απλή αρμονική ταλάντωση.

$Γ_2$ Να γράψετε τη σχέση που δίνει την απομάκρυνση του συσσωματώματος από τη θέση ισορροπίας του σε συνάρτηση με το χρόνο. Να θεωρήσετε θετική φορά τη φορά από το $Α$ προς το $Β$.

$Γ_3$ Να βρείτε τον ρυθμό μεταβολής της δυναμικής ενέργειας του ελατηρίου με σταθερά $k_1$ την χρονική στιγμή αμέσως μετά την πλαστική κρούση.

$Γ_4$ Να βρείτε τον ρυθμό μεταβολής της ορμής του σώματος $Σ_1$ την χρονική στιγμή αμέσως μετά την πλαστική κρούση. Δίνεται $g = 10 \frac{m}{s^2}$ και $ημ30^ο = \frac{1}{2}$

ΘΕΜΑ Δ

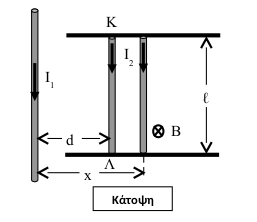
σχήμα

Ευθύγραμμος ακλόνητος αγωγός μεγάλου μήκους διαρρέεται από ρεύμα έντασης $Ι_1=50Α$. Δεύτερος αγωγός $ΚΛ$, μάζας $m = 10g$ και μήκους $ℓ=0.2m$, παράλληλος στον πρώτο, μπορεί να κινείται εφαπτόμενος πάνω σε δύο οριζόντιους μεταλλικούς αγωγούς, χωρίς τριβές, ενώ διαρρέεται από ρεύμα σταθερής έντασης $Ι_2 = Ι_1$. Το επίπεδο που ορίζουν οι δύο αγωγοί είναι οριζόντιο, ενώ βρίσκονται μέσα σε κατακόρυφο ομογενές μαγνητικό πεδίο έντασης $Β$ όπως φαίνεται στο σχήμα. Αν ο αγωγός $ΚΛ$ τοποθετηθεί σε απόσταση $d=0.1m$ από τον ακλόνητο αγωγό $Ι_1$, παραμένει ακίνητος στη θέση αυτή.

$Δ_1$ Ποιο είναι το μέτρο της έντασης $Β$ του κατακόρυφου ομογενούς μαγνητικού πεδίου;

$Δ_2$ Αν ο αγωγός $ΚΛ$ τοποθετηθεί σε απόσταση $x>d$ από τον ακλόνητο αγωγό $Ι_1$, και αφεθεί ελεύθερος, τι είδους κίνηση θα εκτελέσει; Αιτιολογείστε πλήρως την απάντησή σας.

Την χρονική στιγμή $t$ ο αγωγός $ΚΛ$ φτάνει σε απόσταση $2d$ από τον αγωγό μεγάλου μήκους, και έχει ταχύτητα $υ = 0.4 \frac{m}{s}$

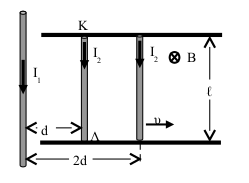
σχήμα

$Δ_3$ Να βρείτε την επιτάχυνση και τον ρυθμό μεταβολής της κινητικής ενέργειας του αγωγού $ΚΛ$ την χρονική στιγμή $t$

$Δ_4$ Την χρονική στιγμή $t'$ που ο αγωγός έχει αποκτήσει ταχύτητα $υ' = 1\frac{m}{s}$ διακόπτουμε τα ρεύματα έντασης $Ι_1$ και $Ι_2$ που διαρρέουν τους αγωγούς και ταυτόχρονα γεφυρώνουμε τους δύο οριζόντιους μεταλλικούς αγωγούς στο αριστερό τους άκρο με αντιστάτες ωμικής αντίστασης $R_1 = 4Ω$ και $R_2 = 16Ω$ που συνδέονται σε σειρά. Να βρεθούν τα ποσά θερμότητας Joule που θα αναπτυχθούν στους αντιστάτες $R_1$ και $R_2$ από την χρονική στιγμή $t'$ έως ότου σταματήσει ο αγωγός $ΚΛ$.

Δίνεται: $k_μ = 10^{-7} \frac{Ν}{Α^2}$

← Previous Archive Next →

blog comments powered by Disqus

Published

05 February 2020

Προσομοίωση 2020 Μουσικό σχολείο Θεσσαλονίκης, 1ο ΓΕΛ Αλεξανδρούπολης, 1ο ΓΕΛ Ευόσμου, 1ο ΓΕΛ Κουφαλίων, 2o ΓΕΛ Καλαμαριάς, 27ο ΓΕΛ Τούμπας, ΓΕΛ Χαλάστρας

Published

Category

Tags