Μέτρηση δύναμης Laplace
Ο ζυγός ρεύµατος αποτελείται από µία εποξική πλακέτα ορθογωνικού σχήµατος όπως φαίνεται στην επόμενη εικόνα:
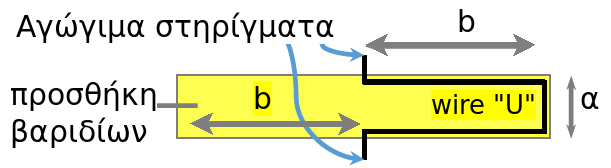
στην οποία έχει δηµιουργηθεί περιµετρικά αγωγός “wire U” που καταλήγει σε άγκιστρα ανάρτησης τοποθετηµένα στη µέση της κάθε µεγάλης πλευράς και μπορεί να περιστρέφεται γύρω από τον άξονα που περνά από τα μέσα των δύο απέναντι πλευρών χωρίς τριβές. Έτσι, η πλακέτα µπορεί να αναρτάται σε κατάλληλα αγώγιµα στηρίγµατα στερεωµένα στην άκρη σωληνοειδούς πηνίου ούτως ώστε το µισό µέρος της να βρίσκεται µέσα στο πηνίο και το άλλο µισό έξω απ΄ αυτό.
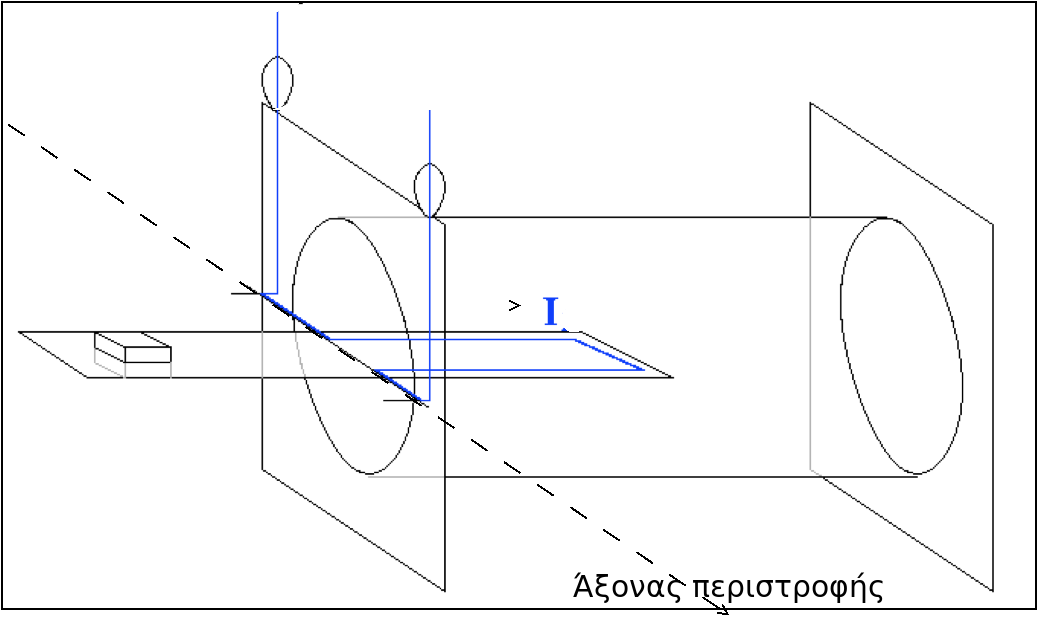
Με τον τρόπο αυτό είναι δυνατόν να διοχετεύεται ρεύµα στο ζυγό \(I\). Το ρεύµα είναι ίδιο με αυτό που διαρρέει το πηνίο (σύνδεση σε σειρά). Όταν ο ζυγός είναι αναρτηµένος στη θέση του και ισορροπηµένος στην οριζόντια θέση, το κοµµάτι του αγωγού που αντιστοιχεί στη στενή πλευρά \(α=4.0 cm\) της πλακέτας έχει θέση κάθετη προς το µαγνητικό πεδίο που δηµιουργείται στο εσωτερικό του πηνίου όταν αυτό διαρρέεται από το ρεύµα \(Ι\). Εάν ταυτόχρονα διαρρέεται από ρεύµα και ο αγωγός του ζυγού ρεύματος, αναπτύσσεται στον αγωγό η δύναµη \(Laplace\) η οποία ανατρέπει την ισορροπία του. Η δύναµη που αναπτύσσεται µπορεί να µετρηθεί ισορροπώντας την πλακέτα στην οριζόντια θέση µε την προσθήκη καταλλήλων βαριδίων και εν συνεχεία µέτρηση του συνολικού βάρους.
Μια ομάδα μαθητών χρησιμοποιεί 20 βαρίδια των \(m = 0,01gr\) το καθένα, ένα τροφοδοτικό 0-20 Volt DC(Direct Current), ένα πολύμετρο για την μέτρηση του ρεύματος \(Ι\), τον ζυγό ρεύματος και καλώδια σύνδεσης για να συνδέσει όλα τα προηγούμενα σε σειρά όπως φαίνεται στο σχήμα:

Οι μαθητές προσθέτουν ανά τέσσερα τα βαρύδια στο μέσον της πλευράς, σε απόσταση \(b\) από τον άξονα περιστροφής της εποξικής πλακέτας και αυτή γέρνει προς τα κάτω. Στη συνέχεια αυξάνουν την τάση εξόδου του τροφοδοτικού μέχρις ότου η εποξική πλακέτα να επανέλθει στην αρχική της θέση. Σημειώνουν τον αριθμό των βαρυδίων και την ένδειξη του αμπερομέτρου \(Ι\) και με την βοήθεια αριθμομηχανής κατασκευάζουν τον παρακάτω πίνακα:
\[\begin{array}{c c c} Αριθμός \quad βαρυδίων & Ι(Α) & I^2(Α^2)\\ 2 & 0.95 & 0.91 \\ 6 & 1.65 & 2.73 \\ 10 & 2.13 & 4.55 \\ 14 & 2.52 & 6.36 \\ 18 & 2.86 & 8.18 \\ \end{array}\]Θεωρήστε δεδομένη την επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\) και την μαγνητική σταθερά \(k_μ = 10^{-7} \frac{N}{Α^2}\). Ο διατιθέµενος εξοπλισµός περιλαµβάνει ένα σωληνοειδές (πηνίο) \(Ν=550\) σπειρών. Το μήκος του σωληνοειδούς είναι περίπου:
\[α. \quad l = 2π \cdot 10^{-2} m\] \[β. \quad l = 4π \cdot 10^{-2} m\] \[γ. \quad l = 6π \cdot 10^{-2} m\]α) Να επιλέξετε την σωστή απάντηση.
β) Να δικαιολογήσετε την επιλογή σας.
Για τον υπολογισμό του συντελεστή διεύθυνσης της ευθείας να γίνει χρήση της σχέσης \(λ = \frac{y_2 - y_1}{x_2 - x_1}\) με τις συντεταγμένες μόνο της αρχικής και της τελικής μέτρησης.
blog comments powered by Disqus