Ηλεκτρομαγνητική επαγωγή
Η οριζόντια μεταλλική ράβδος \(ΚΛ\) μήκους \(l=0.5 m\), μάζας \(m=0.5kg\), έχει ωμική αντίσταση \(R_1 =0.1Ω\) και συγκρατείται ακίνητη πάνω στους κατακόρυφους, άπειρου μήκους, αγώγιμους – αμελητέας αντίστασης – οδηγούς \(Α_{y_1}\) και \(Γ_{y_2}\). Στο χώρο υπάρχει οριζόντιο ομογενές μαγνητικό πεδίο έντασης \(Β=2Τ\), κάθετο στη ράβδο \(ΚΛ\), όπως φαίνεται στο σχήμα.
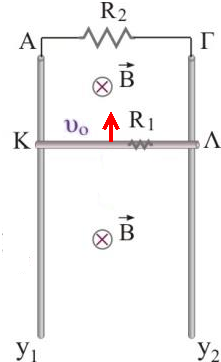
Τα άκρα \(Α\), \(Γ\) συνδέονται με σύρμα αντίστασης \(R_2 =0.4Ω\). Τη χρονική στιγμή \(t=0\), εκτοξεύουμε τη ράβδο \(ΚΛ\) προς τα πάνω με αρχική ταχύτητα \(υ_{αρχ} = 3 \frac{m}{s}\). Μετά από απόσταση \(d_1 = 20 cm\), η ράβδος σταματάει στιγμιαία και στη συνέχεια αρχίζει να κατεβαίνει παραμένοντας οριζόντια και με τα άκρα της συνεχώς σε επαφή με τα κατακόρυφα σύρματα και αποκτά οριακή ταχύτητα, αφού περάσει κάτω από το σημείο εκτόξευσης κατά \(d_2 = 20 cm\). Κατά τη διάρκεια της κίνησής της η ράβδος δέχεται από τους δύο οδηγούς συνολική τριβή μέτρου \(Τ_ρ = 1Ν\).
1. Να προσδιορίσετε τη φορά και την ένταση του επαγωγικού ρεύματος που διαρρέει το κύκλωμα αμέσως μετά την εκτόξευση της ράβδου.
2. Να προσδιορίσετε το είδος της κίνησης που εκτελεί η ράβδος και να γραφεί η εξίσωση της επιτάχυνσης σαν συνάρτηση της ταχύτητας και κατά την άνοδο και κατά την κάθοδο της ράβδου. Να βρείτε τη σταθερή (οριακή) ταχύτητα \(υ_{ορ}\) που αποκτάει.
3. Να υπολογίσετε το επαγωγικό φορτίο που διέρχεται μέσα από μια διατομή της ράβδου \(ΚΛ\) κατά την άνοδό της, από τη χρονική στιγμή \(t = 0\) έως ότου σταματήσει στιγμιαία και κατά την κάθοδό της, από την χρονική στιγμή που σταματά στιγμιαία έως τη χρονική στιγμή που αποκτά την οριακή ταχύτητα.
4. Να υπολογίσετε τη θερμική ενέργεια που εκλύεται σε κάθε ωμικό αντιστάτη και την ενέργεια που χάνεται στο περιβάλλον λόγω της δύναμης της τριβής μέχρι τη στιγμή που η ράβδος αποκτάει την οριακή ταχύτητα.
5. Να υπολογίσετε την ισχύ της δύναμης Laplace, την ηλεκτρική ισχύ που παρέχει η επαγωγική τάση στο κλειστό κύκλωμα, και τον ρυθμό με τον οποίο εκλύεται ενέργεια με τη μορφή θερμότητας λόγω φαινομένου Joule σε κάθε αντιστάτη, τη στιγμή που η ράβδος αποκτάει την οριακή ταχύτητα.
6. Να υπολογίσετε την ισχύ της δύναμης του βάρους και τον ρυθμό μεταβολής της δυναμικής ενέργειας της ράβδου την χρονική στιγμή που η ράβδος αποκτάει την οριακή ταχύτητα.
7. Να υπολογίσετε τη διαφορά δυναμικού στα άκρα της ράβδου και στην αντίσταση \(R_2\) , τη χρονική στιγμή που η δύναμη Laplace είναι ομόρροπη της δύναμης του βάρους και έχει μέτρο \(4Ν\).
8. Να υπολογίσετε τη διαφορά δυναμικού \(V_Α - V_Γ\) όταν ο ρυθμός μεταβολής της ταχύτητας της ράβδου κατά την κάθοδο είναι \(2 \frac{m}{s^2}\)
Θεωρείστε γνωστή την επιτάχυνση της βαρύτητας \(g = 10 \frac{m}{s^2}\)
Απάντηση:
1.
\[Ι_{επ} = 6Α\]2.
\[a = 12 + 4\cdot υ \quad (S.I.), \quad a = 8 - 4 \cdot υ \quad (S.I.), \quad υ_{ορ} = 2 \frac{m}{s}\]3.
\[Q_{ανόδου} = 0.4 C \quad Q_{καθόδου} = 0.8 C\]4.
\[Q_{θερμ1} = 0.33 Joule, \quad Q_{θερμ2} = 1.32 Joule, \quad Q_{θερμTρ} = 0.6 Joule\]5.
\[P_{F_L} = -8 Watt, \quad P_{E_{επ}} = 8 Watt, \quad \frac{ΔQ_{θερμ1}}{Δt} = 1.6 \frac{Joule}{s}, \quad \frac{ΔQ_{θερμ2}}{Δt} = 6.4 \frac{Joule}{s}\]6.
\[P_W = 10 Watt, \quad \frac{dU}{dt} = -10 \frac{Joule}{s}\]7.
\[V_{ΚΛ} = 1,6 Volt, \quad V_2 = 1.6 Volt\]8.
\[V_Α - V_Γ = -1.2 Volt\]blog comments powered by Disqus