Προσομοίωση 2019

ΘΕΜΑ Α

$Α_1$ Το διάγραμμα του σχήματος παριστάνει την ταχύτητα ενός σώματος που εκτελεί απλή αρμονική ταλάντωση σε συνάρτηση με το χρόνο. Στην περίπτωση αυτή

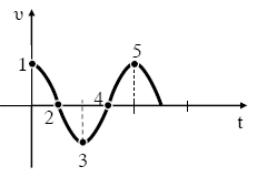
σχήμα

στα σημεία 1 και 5 το σώμα βρίσκεται στη μέγιστη απομάκρυνση.
στα σημεία 2 και 4 το σώμα βρίσκεται στη μέγιστη απομάκρυνση.
στα σημεία 4 και 5 το σώμα βρίσκεται στη θέση ισορροπίας.
στα σημεία 3 και 4 το σώμα βρίσκεται στη θέση ισορροπίας.

⑤

$Α_2$ Στη χορδή μιας κιθάρας, της οποίας τα άκρα είναι σταθερά στερεωμένα, δημιουργείται στάσιμο κύμα. Το μήκος της χορδής είναι ίσο με $L$. Τέσσερα (4) συνολικά σημεία (μαζί με τα άκρα) παραμένουν συνεχώς ακίνητα. Αν $λ$ είναι το μήκος κύματος των κυμάτων από τη συμβολή των οποίων προήλθε το στάσιμο κύμα, τότε

$$L = 3 \cdot λ$$
$$L = \frac{5 \cdot λ}{2}$$
$$L = \frac{3 \cdot λ}{2}$$
$$L = \frac{2 \cdot λ}{3}$$

⑤

$Α_3$ Κατά τη σύνθεση δύο απλών αρμονικών ταλαντώσεων της ίδιας συχνότητας, που γίνονται γύρω από το ίδιο σημείο στην ίδια διεύθυνση και έχουν διαφορά φάσης $180^ο$ , το πλάτος της σύνθετης ταλάντωσης είναι

$$Α_1+Α_2$$
$$ \sqrt{A_1^2+A_2^2}$$
$$|A_1 - A_2|$$
$$ \sqrt{|A_1^2 - A_2^2|}$$

⑤

$Α_4$ Όταν μια μικρή σφαίρα προσπίπτει πλάγια σε κατακόρυφο τοίχο και συγκρούεται με αυτόν ελαστικά, τότε

η κινητική ενέργεια της σφαίρας πριν την κρούση είναι μεγαλύτερη από την κινητική ενέργεια που έχει μετά την κρούση.
η ορμή της σφαίρας δεν μεταβάλλεται κατά την κρούση.
η γωνία πρόσπτωσης της σφαίρας είναι ίση με τη γωνία ανάκλασης.
η δύναμη που ασκεί ο τοίχος στη σφαίρα έχει την ίδια διεύθυνση με την αρχική ταχύτητα της σφαίρας.

⑤

$Α_5$ Να χαρακτηρίσετε τις προτάσεις που ακολουθούν γράφοντας στο τετράδιό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σωστό, αν η πρόταση είναι σωστή, ή τη λέξη Λάθος, αν η πρόταση είναι λανθασμένη.

Η ταχύτητα με την οποία διαδίδεται ένα κύμα σε ένα μέσον, εξαρτάται μόνο από τις ιδιότητες του μέσου που διαταράσσεται, και όχι από το πόσο ισχυρή είναι η διαταραχή.
Καθώς τα αμορτισέρ του αυτοκινήτου παλιώνουν και φθείρονται, η τιμή του b ελαττώνεται και η ταλάντωση διαρκεί περισσότερο.
Το αποτέλεσμα της συμβολής δύο όμοιων κυμάτων στην επιφάνεια υγρού είναι ότι όλα τα σημεία της επιφάνειας είτε παραμένουν διαρκώς ακίνητα είτε ταλαντώνονται με μέγιστο πλάτος.
Κατά την πλαστική κρούση δύο σωμάτων η μηχανική ενέργεια του συστήματος παραμένει σταθερή.
Το έργο της δύναμης που προκαλεί την απόσβεση σε μια φθίνουσα μηχανική ταλάντωση είναι πάντα θετικό.

⑤

ΘΕΜΑ Β

$Β_1$

Οι χρονικές συναρτήσεις της απομάκρυνσης δύο σωμάτων $Σ_1$ και $Σ_2$ που συγκρούονται στη θέση $x = 4m$ φαίνονται στα σχήματα που ακολουθούν. Η μάζα του σώματος $Σ_1$ είναι $m_1 = 1kg$ και η μάζα του σώματος $Σ_2$ είναι $m_2 = 3kg$.

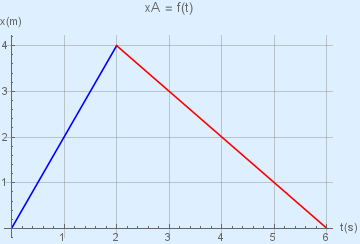
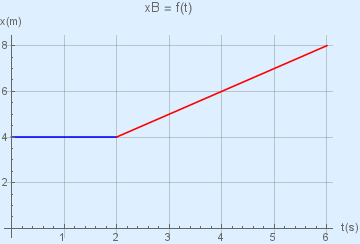
σχήμα

1. Η ορμή του συστήματος των δύο σωμάτων:

διατηρείται
δεν διατηρείται

Να επιλέξετε τη σωστή πρόταση και να δικαιολογήσετε την επιλογή σας.

③

2. Η κινητική ενέργεια του συστήματος των δύο σωμάτων:

διατηρείται
δεν διατηρείται

Να επιλέξετε τη σωστή πρόταση και να δικαιολογήσετε την επιλογή σας.

③

3. Να επιλέξετε το ποσοστό της κινητικής ενέργειας του κινούμενου σώματος που μεταφέρθηκε στο ακίνητο ως αποτέλεσμα της κρούσης

③

$Β_2$

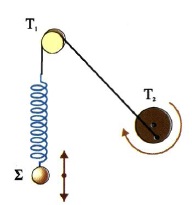
σχήμα

Σφαιρικό δοχείο $Σ$ με νερό έχει συνολικά μάζα $m = 2kg$ είναι δεμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς $k = 50 π^2 \frac{Ν}{m}$. To σύστημα εκτελεί εξαναγκασμένη ταλάντωση, καθώς ο διεγέρτης (το τύμπανο $Τ_2$) περιστρέφεται. Η συχνότητα του διεγέρτη μπορεί να πάρει τιμές από $f = 2Hz$ έως $f = 10Hz$.

1. Είναι δυνατόν μεταβάλλοντας την συχνότητα του διεγέρτη να πετύχουμε συντονισμό του συστήματος;

③

2. Πόσα κιλά νερό πρέπει να αφαιρέσουμε από το δοχείο έτσι ώστε το σύστημα να συντονιστεί στη συχνότητα 5Hz του διεγέρτη;

⑤

$Β_3$

Το άκρο $Ο$ ενός νήματος, το άλλο άκρο $Γ$ του οποίου είναι δεμένο σε κατακόρυφο τοίχο, για $t=0$ τίθεται σε ταλάντωση οπότε κατά μήκος του νήματος διαδίδεται ένας παλμός. Η μορφή του νήματος τη χρονική στιγμή $t_1 =2s$ φαίνεται στο παρακάτω σχήμα.

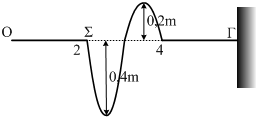
σχήμα

Η περίοδος ταλάντωσης του άκρου $Ο$ είναι

$$Τ = 1s$$
$$T = 2s$$
$$T = \frac{1}{4}s$$

⑧

ΘΕΜΑ Γ

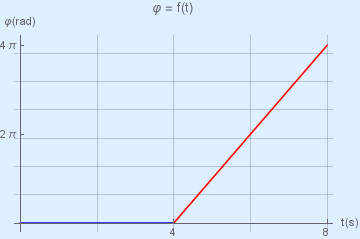
σχήμα

Εγκάρσιο αρμονικό κύμα διαδίδεται σε οριζόντια ελαστική χορδή που εκτείνεται κατά την διεύθυνση του άξονα $x'Ox$.Tο σημείο $O$ της χορδής στη θέση $x=0$, τη χρονική στιγμή $t=0$, έχει μηδενική απομάκρυνση και θετική ταχύτητα. Το κύμα διαδίδεται στην χορδή με ταχύτητα μέτρου $1\frac{m}{s}$. Δίνεται το διάγραμμα της φάσης ενός σημείου $Ν$ της ελαστικής χορδής.

Γνωρίζοντας ότι το σημείο $Ν$ εκτελεί ταλάντωση πλάτους $5cm$

α) Να γράψετε την εξίσωση του κύματος.

⑤

β) Για το ίδιο σημείο $Ν$ να κάνετε την γραφική παράσταση της απομάκρυνσής του σε συνάρτηση με τον χρόνο.

⑤

γ) Να σχεδιάσετε το στιγιότυπο του κύματος την χρονική στιγμή $t=6s$.

⑤

δ) Ποια η διαφορά φάσης του σημείου $Ν$ και του σημείου με τετμημένη $x=+6m$ την χρονική στιγμή $t=7s$;

⑤

ε) Στοιχειώδες τμήμα σχοινιού έχει μάζα $Δm=25g$. Ποιά η μέγιστη δυναμική ενέργεια ταλάντωσης του που προκαλεί το κύμα σε αυτό; Δίνεται $π^2 = 10$

⑤

ΘΕΜΑ Δ

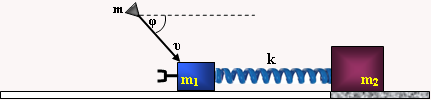
σχήμα

Τα άκρα οριζόντιου αβαρούς ελατηρίου σταθεράς $k=160 \frac{N}{m}$ συνδέονται με δύο σώματα $Σ_1$ και $Σ_2$ με μάζες $m_1 = 6kg$ και $m_2 = 5kg \text{ }$ αντίστοιχα. Το σώμα $Σ_1$ έχει ενσωματωμένη αβαρή πηγή ηχητικών κυμάτων συχνότητας $f_s = 11559.6Hz$ και ηρεμεί πάνω από λείο οριζόντιο επίπεδο. Την χρονική στιγμή $t=0$ ένα τρίτο σώμα με μάζα $m = 4kg$, κινούμενο με ταχύτητα $υ_ο = 10 \frac{m}{s}$ που σχηματίζει γωνία $φ = 60^ο \text{ }$ με το οριζόντιο επίπεδο, συγκρούεται κεντρικά και πλαστικά με το σώμα $Σ_1$ και δεν αναπηδά.

α) Ποια είναι η ελάχιστη τιμή του συντελεστή στατικής τριβής του οριζόντιου επιπέδου που βρίσκεται κάτω από το σώμα $Σ_2$ ώστε αυτό να μην ολισθαίνει.

⑤

β) Να γραφεί η εξίσωση της ταλάντωσης που εκτελεί το συσσωμάτωμα μετά την πλαστική κρούση. Θεωρείστε θετική την φορά κίνησης του συσσωματώματος την χρονική στιγμή $t=0$.

⑤

γ) Να βρεθεί η χρονική στιγμή κατά την οποία το συσσωμάτωμα διέρχεται για πρώτη φορά από την θέση $x = \frac{A}{2} \text{ }$ κινούμενο κατά την αρνητική φορά. Για την συγκεκριμένη χρονική στιγμή να υπολογίσετε τον ρυθμό μεταβολής της κινητικής ενέργειας και τον ρυθμό μεταβολής της ταχύτητας του συσσωματώματος.

⑤

δ) Ποια είναι η ελάχιστη και ποια η μέγιστη συχνότητα που αντιλαμβάνεται λόγω του φαινομένου Doppler ακίνητος παρατηρητής που βρίσκεται στην ευθεία ταλάντωσης του συσσωματώματος αρκετά μακρυά από αυτό. Δίνεται η ταχύτητα του ήχου στον αέρα $340 \frac{m}{s}$.

⑤

ε) Πόσες φορές η συχνότητα που αντιλαμβάνεται ο ακίνητος παρατηρητής συμπίπτει με την συχνότητα $f_s$ που εκπέμπει η πηγή των ηχητικών κυμάτων σε χρόνο $t=12.5π \text{ } s$ από την στιγμή που ξεκινάει να ταλαντώνεται το συσσωμάτωμα.

⑤

Επιμέλεια θεμάτων

Κουκουλέτσος Κωνσταντίνος

Κρομμύδας Αθανάσιος

Πετρίδης Παναγιώτης

Ο κώδικας σε mathematica για τις εικόνες στο θέμα $B1$

f[x] := 2*x
g[x] := 6 - x
 		Show[{Plot[f[x], {x, 0, 2}, PlotStyle -> Blue], 
 		Plot[g[x], {x, 2, 6}, PlotStyle -> Green]}, 
 				PlotRange -> All,
 				GridLines -> Automatic,  
 				Background -> LightBlue, 
 				PlotLabel -> "xA = f(t)", 
 				AxesLabel -> {"t(s)","x(m)"}, 
 				AxesOrigin -> {0, 0}, 
 				Filling -> Automatic]


f[x] := 4
g[x] := x+2
 		Show[{Plot[f[x], {x, 0, 2}, PlotStyle -> Blue], 
 		Plot[g[x], {x, 2, 6}, PlotStyle -> Green]}, 
 				PlotRange -> All,
 				GridLines -> Automatic,  
 				Background -> LightBlue, 
 				PlotLabel -> "xB = f(t)", 
 				AxesLabel -> {"t(s)","x(m)"}, 
 				AxesOrigin -> {0, 0}, 
 				Filling -> Automatic]

Ο κώδικας σε mathematica για την εικόνα στο θέμα $Γ$

f[t] := 0
g[t] :=Pi* t-4*Pi
 		Show[{Plot[f[t], {t, 0, 4}, PlotStyle -> Blue], 
 		Plot[g[t], {t, 4, 8}, PlotStyle -> Green]}, 
 				PlotRange -> All,
 				GridLines -> Automatic,  
 				Background -> LightBlue, 
 				PlotLabel -> "\[CurlyPhi] = f(t)", 
 				AxesLabel -> {"t(s)","\[CurlyPhi](rad)"}, 
 				AxesOrigin -> {0, 0}, 
     			Ticks -> {0, 4,  8},{0, 2Pi,  4Pi},            
 				Filling -> Automatic]

← Previous Archive Next →

blog comments powered by Disqus

Published

03 February 2019

Προσομοίωση 2019 2o ΓΕΛ Καλαμαριάς, 27ο ΓΕΛ Τούμπας, ΓΕΛ Χαλάστρας

Published

Category

Tags